Генетические алгоритмы для задач комбинаторной оптимизации
2.3.4. Матричное представление
Опубликовано достаточно много работ [2,3,4,5,6], где для решения задачи коммивояжера используется представление тура в виде двоичной матрицы, элементы которой  . При этом применяются два основных подхода, которые используют: 1) матрицу смежности; 2) матрицу предшествования, которые мы рассмотрим ниже.
. При этом применяются два основных подхода, которые используют: 1) матрицу смежности; 2) матрицу предшествования, которые мы рассмотрим ниже.
2.3.4.1. Матрица смежности
В матрице смежности элемент 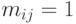 в том и только случае, если в туре после города
в том и только случае, если в туре после города  посещается город
посещается город  (в графе есть ребро от вершины
(в графе есть ребро от вершины  в вершину
в вершину  ). Например, табл.2.1 содержит матрицу смежности для тура
). Например, табл.2.1 содержит матрицу смежности для тура  =(1-2-4-3-8-6-5-7-9) и табл.2.2 – матрицу смежности для тура
=(1-2-4-3-8-6-5-7-9) и табл.2.2 – матрицу смежности для тура  =(1-4-3-6-5-7-2-8-9).
=(1-4-3-6-5-7-2-8-9).
Отметим, что в этом случае каждая строка и столбец матриц содержат одну единицу. Для матрицы смежности можно использовать одно- или двуточечный кроссинговер, где обмен производится, например, столбцами. Но в этом случае необходим дополнительный алгоритм восстановления, который позволяет восстанавливать полученные потомки до полных туров.
Рассмотрим, этот подход на примере двухточечного вертикального кроссинговера с точками скрещивания 2 и 6. При этом производится обмен столбцами (3,4,5,6) матриц смежности (табл.2.1 и табл.2.2). В результате получаем промежуточный результат в виде матриц, которые представлены табл.2.3 и табл.2.4. Обе матрицы не представляют правильных решений, но заметим, что суммарное число единиц в каждой из этих промежуточных матриц правильное (9 единиц).
На первом шаге алгоритма восстановления передвигаем 1 в матрице таким образом, чтобы каждая строка и столбец имели одну единицу. Например, в матрице табл.2.3 первая строка имеет две 1 (вместо одной). Поэтому "передвинем"  в позицию
в позицию  , а элемент
, а элемент  в
в 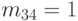 , аналогично
, аналогично  в
в  . В результате после выполнения первого этапа алгоритма восстановления получаем правильный тур для первого потомка
. В результате после выполнения первого этапа алгоритма восстановления получаем правильный тур для первого потомка 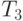 =(1-2-8-4-3-6-5-7-9), в то время как второй потомок содержит два подтура
=(1-2-8-4-3-6-5-7-9), в то время как второй потомок содержит два подтура 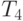 =(1-6-5-7-2-8-9) (3-4).
=(1-6-5-7-2-8-9) (3-4).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Поэтому на втором этапе алгоритма восстановления обрабатываем только второй потомок. При этом необходимо разорвать частичные подтуры и объединить их в единый правильный тур. Это можно сделать, например, с помощью ребра 2-4, которое присутствует у одного из родителей. В результате получаем полный тур для второго потомка  =(1-6-5-7-2-4-3-8-9).
=(1-6-5-7-2-4-3-8-9).
