Генетические алгоритмы для задач комбинаторной оптимизации
2.2. Задача о покрытии
Задано множество элементов  и множество подмножеств
и множество подмножеств 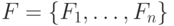 этого множества
этого множества  . Необходимо найти минимальное число подмножеств из
. Необходимо найти минимальное число подмножеств из  таких, чтобы объединение этих подмножеств содержало все элементы множества
таких, чтобы объединение этих подмножеств содержало все элементы множества  . Задача имеет простую экономическую интерпретацию: пусть, например, имеется некоторое количество клиентов и для их обслуживания необходимо выбрать некоторое количество сервисных центров. Требуется найти минимальное число центров, способных обслуживать всех клиентов.
. Задача имеет простую экономическую интерпретацию: пусть, например, имеется некоторое количество клиентов и для их обслуживания необходимо выбрать некоторое количество сервисных центров. Требуется найти минимальное число центров, способных обслуживать всех клиентов.
Очевидно, здесь решение можно также представить двоичным вектором
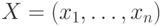 , где
, где
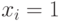 , если подмножество
, если подмножество 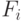 входит в покрытие;
входит в покрытие;
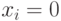 , если
, если 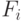 не входит в покрытие;
не входит в покрытие;
и при этом
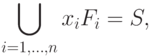
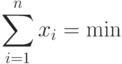
Поскольку решение задачи, как было показано выше, представляется двоичным вектором, то при его поиске можно использовать простой ГА со стандартными операторами кроссинговера и мутации.
2.3. Задача коммивояжера
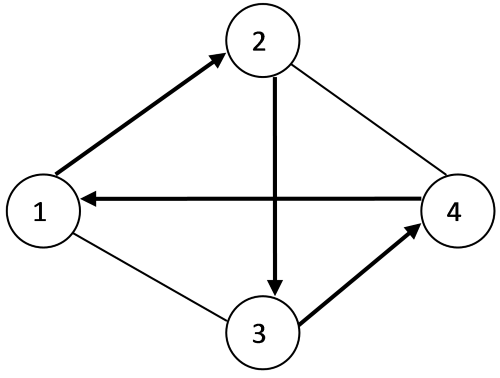
Напомним неформальную постановку этой классической задачи. Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по одному разу в некотором порядке все города и вернуться в исходный город. На рис.2.1 приведен пример задачи для четырех городов.
Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?
В формальной постановке задачи коммивояжера (ЗК): имеется полный взвешенный ориентированный граф  без петель с множеством вершин
без петель с множеством вершин 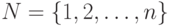 ; веса всех дуг неотрицательны; в этом графе требуется найти гамильтонов цикл с минимальной длиной. Исходная информация по ЗК представляется в виде
; веса всех дуг неотрицательны; в этом графе требуется найти гамильтонов цикл с минимальной длиной. Исходная информация по ЗК представляется в виде  матрицы
матрицы ![S=[s_{i,j}],s_{i,j}](/sites/default/files/tex_cache/bec6a6c4766b1375f4d2336427ec5a37.png) вес дуги
вес дуги 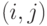 графа
графа  ,
, 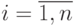 ,
, 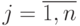 ,
,  ; все элементы главной диагонали нулевые
; все элементы главной диагонали нулевые  (но в некоторых постановках полагаются
(но в некоторых постановках полагаются 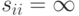 ). Обычно
). Обычно 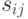 интерпретируется как расстояние между городами
интерпретируется как расстояние между городами  и
и  . С учетом других возможных интерпретаций на матрицу
. С учетом других возможных интерпретаций на матрицу  требование симметричности не налагается. Например, в случае интерпретации
требование симметричности не налагается. Например, в случае интерпретации 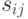 как стоимости проезда, в общем случае может быть
как стоимости проезда, в общем случае может быть  . В общем случае не считается обязательным и выполнение неравенства треугольника
. В общем случае не считается обязательным и выполнение неравенства треугольника 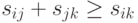 .
.
Тур коммивояжера может быть описан циклической перестановкой 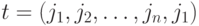 , причём все
, причём все 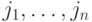 – попарно различны; повторяющийся в начале и в конце номер города
– попарно различны; повторяющийся в начале и в конце номер города 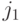 , показывает, что перестановка циклическая. Пространством поиска решений этой задачи является множество перестановок
, показывает, что перестановка циклическая. Пространством поиска решений этой задачи является множество перестановок  городов. Любая простая (одиночная) перестановка
городов. Любая простая (одиночная) перестановка  городов даёт решение, являющееся полным туром из
городов даёт решение, являющееся полным туром из  городов. Оптимальным решением является перестановка, которая даёт минимальную стоимость тура. Очевидно, размерность пространства поиска для несимметричной задачи равна
городов. Оптимальным решением является перестановка, которая даёт минимальную стоимость тура. Очевидно, размерность пространства поиска для несимметричной задачи равна  . Известно, что эта задача является NP – полной, т.е. переборной. Она имеет многочисленные практические приложения, в которых число "городов" может быть достаточно большим. Например, при производстве сложных деталей задача сверления отверстий может иметь сотни и тысячи "городов". При производстве СБИС возникают задачи (например, по внесению примесей в полупроводник) с числом "городов" около миллиона. За последние десятилетия разработано достаточно много алгоритмов решения этой задачи, дающих субоптимальное решение. В последнее десятилетие эта задача является базовой для исследования ГА в области комбинаторной оптимизации.
. Известно, что эта задача является NP – полной, т.е. переборной. Она имеет многочисленные практические приложения, в которых число "городов" может быть достаточно большим. Например, при производстве сложных деталей задача сверления отверстий может иметь сотни и тысячи "городов". При производстве СБИС возникают задачи (например, по внесению примесей в полупроводник) с числом "городов" около миллиона. За последние десятилетия разработано достаточно много алгоритмов решения этой задачи, дающих субоптимальное решение. В последнее десятилетие эта задача является базовой для исследования ГА в области комбинаторной оптимизации.
Очевидно, что двоичное представление тура при решении ЗК нецелесообразно. Действительно если мы интересуемся оптимальной перестановкой городов, т.е. 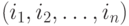 и используем двоичное представление в виде одного бинарного вектора, то изменение даже в одном бите двоичного кода перестановки может дать двоичный вектор, не принадлежащий к области решения, т.е. не являющейся перестановкой
и используем двоичное представление в виде одного бинарного вектора, то изменение даже в одном бите двоичного кода перестановки может дать двоичный вектор, не принадлежащий к области решения, т.е. не являющейся перестановкой  городов.
городов.
Для решения ЗК с помощью генетических алгоритмов разработаны специальные методы представления (кодирования) решений и соответствующие проблемно-ориентированные генетические операторы [2,3,4]. В основном используются три способа представления тура при решении ЗК с использованием ГА: 1) представление порядка; 2) представление соседства; 3) представление путей. Для каждого из этих представлений разработаны свои "генетические" операторы. Оператор мутации относительно легко определить на этих представлениях в виде одиночной перестановки соседних городов в туре. Поэтому в дальнейшем мы, в основном, рассмотрим операторы кроссинговера.
2.3.1. Упорядоченное представление.
В этом случае тур представляется списком из n городов, где  -й элемент списка имеет номер от 1 до
-й элемент списка имеет номер от 1 до 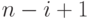 . При этом используется базовый упорядоченный список городов
. При этом используется базовый упорядоченный список городов  , который служит для ссылок упорядоченного представления. Фактически мы рассматривали этот метод кодирования решения при решении задачи об укладке рюкзака.
, который служит для ссылок упорядоченного представления. Фактически мы рассматривали этот метод кодирования решения при решении задачи об укладке рюкзака.
Рассмотрим его на конкретном примере тура  = (1-2-4-3-8-5-9-6-7), для которого упорядоченный список
= (1-2-4-3-8-5-9-6-7), для которого упорядоченный список  = (1 2 3 4 5 6 7 8 9). Тогда данный тур при этом упорядоченном списке представляется следующим списком ссылок
= (1 2 3 4 5 6 7 8 9). Тогда данный тур при этом упорядоченном списке представляется следующим списком ссылок  =(1 1 2 1 4 1 3 1 1), который интерпретируется следующим образом. Здесь жирным курсивом выделен текущий указатель в списке
=(1 1 2 1 4 1 3 1 1), который интерпретируется следующим образом. Здесь жирным курсивом выделен текущий указатель в списке  .
.
Первый номер из списка  равен 1, поэтому помещаем в тур 1-й город из базового списка
равен 1, поэтому помещаем в тур 1-й город из базового списка  , удаляем его из
, удаляем его из  и сдвигаем указатель по
и сдвигаем указатель по  . Тогда получаем:
. Тогда получаем:
тур  =(1), базовый список
=(1), базовый список 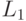 = (2 3 4 5 6 7 8 9) , указатель
= (2 3 4 5 6 7 8 9) , указатель  =(1 1 2 1 4 1 3 1 1).
=(1 1 2 1 4 1 3 1 1).
Следующий номер по указателю  также равен 1, поэтому снова помещаем в тур 1-й город из базового списка
также равен 1, поэтому снова помещаем в тур 1-й город из базового списка  , удаляем его из
, удаляем его из  и сдвигаем указатель по
и сдвигаем указатель по  .
.
В результате получаем :
текущий тур  =( 1-2),
=( 1-2), 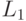 = (3 4 5 6 7 8 9) и указатель в e сдвигается на третью позицию
= (3 4 5 6 7 8 9) и указатель в e сдвигается на третью позицию  = (1 1 2 1 4 1 3 1 1). Следующий номер списка е равен 2, поэтому мы берем и удаляем 2-й город из текущего базового списка
= (1 1 2 1 4 1 3 1 1). Следующий номер списка е равен 2, поэтому мы берем и удаляем 2-й город из текущего базового списка  и добавляем его в тур и передвигаем указатель по
и добавляем его в тур и передвигаем указатель по  . Имеем:
. Имеем:
текущий тур 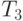 =(1-2-4),
=(1-2-4),  = (3 5 6 7 8 9),
= (3 5 6 7 8 9),  = (1 1 2 1 4 1 3 1 1).
= (1 1 2 1 4 1 3 1 1).
Продолжая этот процесс, в результате декодирования по данному коду  =(1 1 2 1 4 1 3 1 1), базовому списку
=(1 1 2 1 4 1 3 1 1), базовому списку  = (1 2 3 4 5 6 7 8 9) будет построен тур
= (1 2 3 4 5 6 7 8 9) будет построен тур  = (1-2-4-3-8-5-9-6-7) .
= (1-2-4-3-8-5-9-6-7) .
Основное преимущество упорядоченного представления в том, что в этом случае работает классический кроссинговер (над векторами целых чисел). То есть для двух допустимых решений кроссинговер производит два допустимых решения – потомка.
Например, для родителей
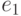 = (1 1 2 1 | 4 1 3 1 1) и
= (1 1 2 1 | 4 1 3 1 1) и 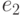 = (5 1 5 5 | 5 3 3 2 1),
= (5 1 5 5 | 5 3 3 2 1),
которые соответствуют турам
 =(1-2-4-3-8-5-9-6-7) и
=(1-2-4-3-8-5-9-6-7) и  =(5-1-7-8-9-4-6-3-2),
=(5-1-7-8-9-4-6-3-2),
имеем следующих потомков при скрещивании
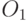 = (1 1 2 1 5 3 3 2 1) и
= (1 1 2 1 5 3 3 2 1) и 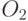 = (5 1 5 5 4 1 3 1 1),
= (5 1 5 5 4 1 3 1 1),
которые представляют туры
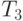 =(1-2-4-3-9-7-8-6-5) и
=(1-2-4-3-9-7-8-6-5) и 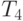 =(5-1-7-8-6-2-9-3-4).
=(5-1-7-8-6-2-9-3-4).
Очевидно, что частичные туры слева от точки кроссинговера не изменяются, в тоже время частичные туры справа от нее разрываются случайным образом (сохраняя корректность решения). К сожалению, машинные эксперименты по решению ЗК на основе этого представления решений с использованием классического кроссинговера показывают посредственные результаты [4].