Генетические алгоритмы для задач комбинаторной оптимизации
2.3.2. Представление соседства
В этом случае тур представляется списком соседних городов. Город  находится в позиции
находится в позиции  если и только если в туре после города
если и только если в туре после города  посещается город
посещается город  , что показано на рис.2.2
, что показано на рис.2.2
Например, вектор 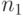 =(2 4 8 3 9 7 1 5 6) представляет следующий тур
=(2 4 8 3 9 7 1 5 6) представляет следующий тур  =(1-2-4-3-8-5-9-6-7). При этом любой тур имеет единственное представление списком соседства. Однако некоторые "списки соседей" могут представлять "неправильные" туры. Например, список соседства
=(1-2-4-3-8-5-9-6-7). При этом любой тур имеет единственное представление списком соседства. Однако некоторые "списки соседей" могут представлять "неправильные" туры. Например, список соседства 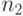 =(2 4 8 1 9 3 5 7 6) содержит "частичный" тур
=(2 4 8 1 9 3 5 7 6) содержит "частичный" тур  =(1-2-4-1). Поэтому представление списком соседей не поддерживает классический оператор кроссинговера, поскольку при перестановке частей списков могут получаться неправильные ("частичные") туры. В этом случае необходим некоторый алгоритм восстановления полного тура.
=(1-2-4-1). Поэтому представление списком соседей не поддерживает классический оператор кроссинговера, поскольку при перестановке частей списков могут получаться неправильные ("частичные") туры. В этом случае необходим некоторый алгоритм восстановления полного тура.
Для данного способа кодирования решения были предложены и исследованы 3 основных оператора кроссинговера: 1) обмен ребер (дуг) графа; 3) обмен подтуров; 3) эвристический кроссинговер [2,3,4]. Далее рассмотрим их детально.
- Обмен ребер.
Этот тип кроссинговера строит потомка (случайным) выбором ребра (пары городов
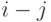 ) из первого родителя, затем выбором соответствующего ребра из второго родителя и т.д. Оператор наращивает тур выбором ребер из различных родителей. Если новое ребро (взятое у одного из родителей) образует преждевременный (частичный) цикл в текущем (ещё не полном) туре, то оператор выбирает (случайно) вместо этого ребра одно из оставшихся ребер, которое не дает преждевременного цикла.
) из первого родителя, затем выбором соответствующего ребра из второго родителя и т.д. Оператор наращивает тур выбором ребер из различных родителей. Если новое ребро (взятое у одного из родителей) образует преждевременный (частичный) цикл в текущем (ещё не полном) туре, то оператор выбирает (случайно) вместо этого ребра одно из оставшихся ребер, которое не дает преждевременного цикла.Например, для 2-х родителей
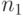 = (2 3 8 7 9 4 1 5 6), представляющего тур
= (2 3 8 7 9 4 1 5 6), представляющего тур  =(1-2-3-8-5-9-6-4-7-1), и
=(1-2-3-8-5-9-6-4-7-1), и 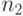 = (7 5 1 6 9 2 8 4 3), представляющего тур
= (7 5 1 6 9 2 8 4 3), представляющего тур  =(1-7-8-4-6-2-5-9-3-1), получаем следующего потомка
=(1-7-8-4-6-2-5-9-3-1), получаем следующего потомка 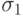 = (2 5 8 7 9 4 3 1 6). Здесь произведен обмен (случайный) ребер
= (2 5 8 7 9 4 3 1 6). Здесь произведен обмен (случайный) ребер  во второй позиции, далее при попытке обмена
во второй позиции, далее при попытке обмена  в седьмой позиции возникает конфликт (два ребра входят в 8), поэтому случайно выбирается 3 в позиции 7 ( из оставшихся 6, 1, 3), 1 – в позиции 8 и 6 в позиции 9. В результате порождается потомок
в седьмой позиции возникает конфликт (два ребра входят в 8), поэтому случайно выбирается 3 в позиции 7 ( из оставшихся 6, 1, 3), 1 – в позиции 8 и 6 в позиции 9. В результате порождается потомок 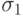 , который соответствует туру
, который соответствует туру 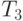 =(1-2-5-9-6-4-7-3-8-1).
=(1-2-5-9-6-4-7-3-8-1). - Обмен подтуров.
Этот оператор строит потомки путём выбора (случайной длины) подтура из первого родителя, затем выбора подтура (опять случайной длины) из второго родителя и их обмена. Как и ранее, в случае конфликта оператор случайно выбирает другое ребро (город) из не вошедших в построенный тур.
- Эвристическое скрещивание.
Данный оператор строит потомка случайным выбором города в качестве начальной точки для формирования тура. Затем сравниваются два ребра, исходящие из этого города, имеющихся в двух родителях, и из них выбирается лучшее с меньшей стоимостью. Полученный город (в него входит выбранное ребро на предыдущем этапе), используется в качестве начальной точки при выборе следующего ребра и т.д. Как и ранее, в случае возникновения преждевременного цикла, следующий город выбирается случайно из городов, еще не вошедших в текущий тур. Известна следующая модификация этого оператора.
Если оптимальное (с меньшей стоимостью) ребро дает преждевременный цикл в потомке, то проверяется альтернативное ребро (с большей стоимостью) на генерацию преждевременного цикла. Если это ребро не генерирует цикл, то оно включается в тур, иначе выбирается минимальное из  ребер (где
ребер (где  –параметр пула выбора) случайно выбранных из оставшихся городов.
–параметр пула выбора) случайно выбранных из оставшихся городов.
Преимущество этого кодирования в том, что в этом случае анализ схем (шаблонов) можно проводить по аналогии с двоичным случаем. Например, схема (* * * 3 *7 * * *) представляет множество всех туров с ребрами (4-3) и (6-7). Однако основной недостаток этого представления в весьма посредственных результатах тестовых задач для всех трех рассмотренных операторов. Кроссинговер обмена ребер часто разрывает хорошие туры при обмене ребер родителей. Кроссинговер обмена подтуров даёт лучшие результаты, чем предыдущий, так как "отношение разрыва" здесь меньше. Эвристический оператор даёт несколько лучшие результаты за счет учета стоимости исходящих ребер и локального выбора лучшего варианта из двух возможных. Однако эксперименты показывают также посредственные результаты [4].
2.3.3. Представление путей.
Это представление, возможно, самое естественное для тура. Например, тур (5-1-7-8-9-4-6-2-3) представляется просто упорядоченным списком (5 1 7 8 9 4 6 2 3) городов, входящих в тур.
Для данного представления были определены и исследованы три типа кроссинговера [2,3,4]:
- частично соответствующий (partially-mapped - РМХ);
- упорядоченный ОК (order - ОХ);
- циклический ОК (cycle - CХ).
Рассмотрим их по порядку.
Частично соответствующий ОК (РМХ) строит потомок путем выбора последовательности тура из одного родителя и сохранения порядка и позиции городов из другого родителя насколько это возможно. Подпоследовательность из тура выбирается случайно с помощью двух "секущих" точек, которые служат границами для операции обмена. Например, для родителей 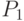 =(1 2 3 | 4 5 6 7| 8 9) и
=(1 2 3 | 4 5 6 7| 8 9) и 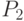 = (4 5 2 | 1 8 7 6 | 9 3) потомок строится следующим образом.
= (4 5 2 | 1 8 7 6 | 9 3) потомок строится следующим образом.
Сначала производим обмен выделенными подтурами и в результате получаем  = (X X X | 1 8 7 6 | X X) и
= (X X X | 1 8 7 6 | X X) и  = (X X X | 4 5 6 7 | X X), где "X" означает еще незаполненную позицию (допускающую произвольное значение). Этот обмен определяет также отображение
= (X X X | 4 5 6 7 | X X), где "X" означает еще незаполненную позицию (допускающую произвольное значение). Этот обмен определяет также отображение  . Далее (вместо "Х") вставляем города из исходных родителей, для которых нет конфликтов (не образуются преждевременный цикл):
. Далее (вместо "Х") вставляем города из исходных родителей, для которых нет конфликтов (не образуются преждевременный цикл): 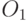 = (X 2 3 | 1 8 7 6 | X 9),
= (X 2 3 | 1 8 7 6 | X 9), 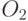 = (X X 2 | 4 5 6 7 | 9 3).
= (X X 2 | 4 5 6 7 | 9 3).
Далее первый "Х" в 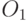 , заменяем на "4" согласно отображению
, заменяем на "4" согласно отображению 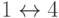 . Аналогично второй "Х" в потомке
. Аналогично второй "Х" в потомке 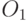 заменяется "5", и во втором потомке
заменяется "5", и во втором потомке 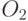 оставшиеся неопределенные позиции "Х" заменяются соответственно на 1 и 8. В результате получаем два потомка:
оставшиеся неопределенные позиции "Х" заменяются соответственно на 1 и 8. В результате получаем два потомка: 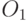 = (4 2 3 | 1 8 7 6 | 5 9) и
= (4 2 3 | 1 8 7 6 | 5 9) и 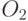 = ( 1 8 2 | 4 5 6 7 | 9 3).
= ( 1 8 2 | 4 5 6 7 | 9 3).
Упорядоченный ОК строит потомок выбором подтура из одного родителя и сохранением относительного порядка городов из другого родителя. Например, для родителей 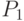 = (1 2 3 | 4 5 6 7 | 8 9),
= (1 2 3 | 4 5 6 7 | 8 9), 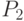 = (4 5 2 | 1 8 7 6 | 9 3) потомок строится следующим образом.
= (4 5 2 | 1 8 7 6 | 9 3) потомок строится следующим образом.
Сначала сегменты между двумя секущими точками копируется в потомки: 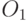 = (X X X | 4 5 6 7 | X X),
= (X X X | 4 5 6 7 | X X), 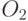 = (X X X | 1 8 7 6 | X X).
= (X X X | 1 8 7 6 | X X).
Далее, в первом родителе, начиная со второй секущей точки, копируются города из другого родителя, пропуская уже присутствующие в построенном подтуре. По достижению конца списка этот процесс продолжается с первой позиции и до первой точки сечения (по кольцу).
Для нашего примера после второй точки сечения во втором родителе мы имеем следующую последовательность: 9 – 3 – 4 – 5 – 2 – 1 – 8 – 7 – 6. Удаляем из нее города 4, 5, 6, 7, поскольку они уже есть в первом потомке, и в результате получаем последовательность 9 – 3 – 2 – 1 – 8. Ее мы помещаем в первый потомок, начиная со второй точки сечения (по кольцу) и получаем потомок 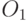 = (2 1 8 | 4 5 6 7 | 9 3). Аналогично получаем второго потомка
= (2 1 8 | 4 5 6 7 | 9 3). Аналогично получаем второго потомка 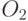 = (3 4 5 | 1 8 7 6 | 9 2).
= (3 4 5 | 1 8 7 6 | 9 2).
Оператор кроссинговера ОХ опирается на то, что при представлении тура прежде всего важен порядок городов, например, два тура (9–3–4–5–2–1–8–7–6) и (4–5–2–1–8–7–6–9–3) идентичны.
Циклический ОК строит потомки таким образом, что каждый город вместе со своей позицией идет от одного из родителей. Например, для родителей 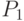 = (1 2 3 4 5 6 7 8 9) и
= (1 2 3 4 5 6 7 8 9) и 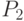 = (4 1 2 8 7 6 9 3 5) сначала получаем путем выбора первого города из родителя
= (4 1 2 8 7 6 9 3 5) сначала получаем путем выбора первого города из родителя 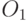 = (1X X X X X X X X). Выбор следующего города определяет текущая позиция второго родителя. В нашем примере это город 4, что дает
= (1X X X X X X X X). Выбор следующего города определяет текущая позиция второго родителя. В нашем примере это город 4, что дает 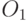 = (1 X X 4 X X X X X). Город 4 в свою очередь имплицирует город 8 (из второго родителя), что дает
= (1 X X 4 X X X X X). Город 4 в свою очередь имплицирует город 8 (из второго родителя), что дает 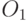 = (1 X X 4 X X X 8 X).
= (1 X X 4 X X X 8 X).
Аналогично получаем города 3, 2 в 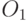 = (1 2 3 4 X X X 8 X). Здесь мы вынуждены прервать этот процесс, так как выбор
= (1 2 3 4 X X X 8 X). Здесь мы вынуждены прервать этот процесс, так как выбор 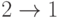 ведет к преждевременному циклу. Поэтому оставшиеся города берутся из другого родителя
ведет к преждевременному циклу. Поэтому оставшиеся города берутся из другого родителя 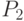 (с сохранением порядка) и в результате получаем потомков
(с сохранением порядка) и в результате получаем потомков 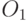 = (1 2 3 4 7 6 9 8 5 ) и
= (1 2 3 4 7 6 9 8 5 ) и 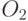 = (4 1 2 8 5 6 7 3 9). Таким образом, оператор ОК СХ сохраняет абсолютные позиции потомков и родителей.
= (4 1 2 8 5 6 7 3 9). Таким образом, оператор ОК СХ сохраняет абсолютные позиции потомков и родителей.

