|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Кратчайшие пути
Отрицательные веса
Теперь обратимся к проблеме обработки отрицательных весов в задачах поиска кратчайших путей. Возможно, отрицательные веса ребер покажутся неестественными, поскольку на протяжении большей части этой главы мы на наглядных примерах привыкли, что веса представляют расстояния или стоимости. Однако, как было показано в разделе 21.6, отрицательные веса ребер естественно возникают, когда к задаче поиска кратчайших путей сводятся другие задачи. Отрицательные веса - это не просто математическая абстракция; напротив, они существенно расширяют применимость задач поиска кратчайших путей в качестве модели для решения других задач. Эта потенциальная польза побуждает нас искать эффективные алгоритмы для решения сетевых задач, в которых возможны отрицательные веса.
На рис. 21.26 показан небольшой пример, который демонстрирует влияние введения отрицательных весов в задаче о наиболее коротких путях в сети. Возможно, наиболее важный эффект состоит в том, что при наличии отрицательных весов наиболее короткие пути с малыми весами часто содержат больше ребер, чем пути с более высокими весами. В случае положительных весов мы старались искать пути напрямик; однако при наличии отрицательных весов мы ищем обходные пути, которые содержат столько ребер с отрицательными весами, сколько мы сможем отыскать. Этот эффект переворачивает наше наглядное понимание поиска " коротких " путей, которое необходимо для понимания алгоритмов, так что нам потребуется преодолеть этот интуитивный барьер и рассмотреть данную задачу на базовом абстрактном уровне.
Взаимосвязь между кратчайшими путями в сетях и гамильтоновыми путями в графах, показанная при доказательстве леммы 21.18, перекликается с наблюдением, что поиск путей низкого веса (которые мы называем " короткими " ) равноценен поиску путей с большим количеством ребер (которые можно считать " длинными " ). При наличии отрицательных весов мы ищем скорее длинные пути, нежели короткие.
Первая мысль, которая приходит на ум, чтобы исправить ситуацию - это найти наименьший (самый отрицательный) вес ребра, затем добавить абсолютное значение этого числа ко всем весам ребер, чтобы получить сеть без отрицательных весов. Этот наивный способ вообще не работает из-за того, что кратчайшие пути в новой сети никак не связаны с кратчайшими путями в прежней сети.
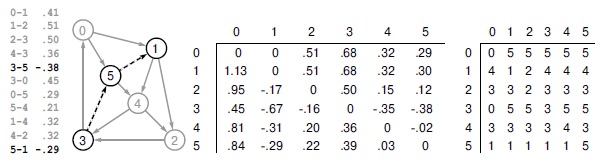
Это та же демонстрационная сеть, что и сеть с рис. 21.1, только веса ребер 3-5 и 5-1 являются отрицательными. Естественно, данное изменение существенно влияет на структуру кратчайших путей, что легко увидеть, сравнивая матрицы расстояний и путей справа с соответствующими матрицами на рис. 21.9. Например, кратчайший путь из 0 в 1 в этой сети - это путь 0-5-1, который имеет длину 0, а кратчайшим путем из 2 в 1 является путь 2-3-5-1 с длиной -0.17.
Например, в сети, приведенной на рис. 21.26, кратчайший путь из 4 в 2 - это путь 4-3-5-1-2. Если увеличить веса всех ребер в графе на 0.38, чтобы сделать их все положительными, вес этого пути увеличится с 0.20 до 1.74. Однако вес 4-2 возрастет с 0.32 лишь до 0.70, так что кратчайшим путем из 4 в 2 станет это ребро. Чем больше ребер содержит путь, тем больше он " потяжелеет " от такого преобразования, поэтому результат с точки зрения предыдущего абзаца как раз противоположен тому, что требуется. Но даже если этот наивный подход не работает, идея преобразования сети в эквивалентную без отрицательных весов, но с теми же кратчайшими путями, вполне достойна внимания; в конце раздела мы рассмотрим алгоритм на основе этой идеи.
Все наши алгоритмы поиска кратчайших путей до сих пор содержали одно из двух ограничений на задачу кратчайших путей, которые позволяли получить эффективное решение: они запрещали либо циклы, либо отрицательные веса. Существуют ли менее строгие ограничения, которые можно было бы наложить на сети, содержащие как циклы, так и отрицательные веса, и все-таки получить разрешимые задачи кратчайших путей? Мы коснулись ответа на этот вопрос в начале главы, когда нам понадобилось добавить требование, что для того, чтобы задача имела бы смысл в случае наличия отрицательных циклов, пути должны быть простыми. Возможно, нам следует ограничиться рассмотрением сетей, которые не имеют таких циклов?
Кратчайшие пути в сетях без отрицательных циклов. Для заданной сети, которая может содержать ребра с отрицательными весами, но не содержит циклов отрицательного веса, требуется решить одну из следующих задач: найти кратчайший путь, соединяющий две заданных вершины (задача поиска кратчайшего пути), найти кратчайшие пути из заданной вершины во все другие вершины (задача с одним истоком) или найти кратчайшие пути, соединяющие все пары вершин (задача для всех пар вершин).
Доказательство леммы 21.18 оставляет возможность построения эффективных алгоритмов решения этой задачи, поскольку оно теряет смысл в отсутствие отрицательных циклов. Чтобы решить задачу поиска гамильтонова пути, необходимо иметь возможность решать задачи поиска кратчайших путей в сетях с огромным количеством отрицательных циклов.
Кроме того, многие практические задачи сводятся в точности к задаче поиска кратчайших путей в сетях, которые не содержат отрицательных циклов. Мы уже видели один такой пример.
Лемма 21.19. Задача календарного планирования с конечными сроками сводится к задаче поиска кратчайших путей в сетях, которые не содержат отрицательных циклов.
Доказательство. Рассуждения из доказательства леммы 21.15 показывают, что построение в доказательстве леммы 21.16 приводит к сетям, не содержащим отрицательных циклов. Из задачи календарного планирования мы создаем задачу разностных ограничений с переменными, которые соответствуют моментам начала работ, а из задачи разностных ограничений мы создаем сеть. Затем мы меняем знаки всех весов, чтобы перейти от задачи поиска наиболее длинных путей к задаче поиска кратчайших путей - преобразование, которое обращает знаки всех неравенств. Любой простой путь в сети из i в j соответствует последовательности неравенств, включающих переменные. Свертывая эти неравенства, получаем из существования такого пути, что 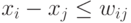 , где wij - сумма весов на пути из i в j. Отрицательный цикл соответствует 0 в левой части этого неравенства и отрицательному значению в правой части, т.е. такой цикл не может существовать.
, где wij - сумма весов на пути из i в j. Отрицательный цикл соответствует 0 в левой части этого неравенства и отрицательному значению в правой части, т.е. такой цикл не может существовать. 
Как мы отмечали, когда впервые обсуждали задачу календарного планирования в разделе 21.6, это утверждение неявно предполагает, что наши задачи календарного планирования являются разрешимыми (т.е. имеют решение). На практике не следует делать подобное допущение, и часть вычислительных затрат уйдет на определение разрешимости задачи календарного планирования с конечными сроками. В построении доказательства леммы 21.19 отрицательный цикл в сети означает, что задача невыполнима, поэтому данная задача соответствует следующей.
Обнаружение отрицательных циклов. Содержит ли данная сеть отрицательный цикл? Если да, то нужно найти один такой цикл.
С одной стороны, эта задача не обязательно простая (простые алгоритмы проверки циклов для орграфов неприменимы); с другой стороны, она не обязательно сложная (неприменимо и сведение из леммы 21.16 из задачи поиска гамильтонова пути). Поэтому вначале нужно разработать алгоритм решения этой задачи.
В приложении календарного планирования с конечными сроками отрицательные циклы соответствуют ошибочным условиям, которые, видимо, не должны встречаться часто, но наличие которых все же необходимо проверять. Мы могли бы даже разработать алгоритмы, которые удаляют ребра, чтобы разорвать отрицательный цикл, и делают так, пока не останется ни одного. В других приложениях обнаружение отрицательных циклов является основной целью, как в следующем примере.
Арбитражные операции (валютные спекуляции). Многие газеты печатают таблицы курсов мировых валют (см., например, рис. 21.27). Такие таблицы можно рассматривать как представления матрицами смежности для полных сетей. Ребро s-t с весом x означает, что можно конвертировать одну единицу валюты s в x единиц валюты t. Пути в сети задают многошаговые конверсии. Например, если существует также ребро t-w с весом у, то путь s-t-w представляет способ, позволяющий конвертировать одну единицу валюты s в xy единиц валюты w. Можно было бы ожидать, что xy равно весу ребра s-w во всех случаях, однако подобные таблицы являются сложной динамичной системой, где такая последовательность отнюдь не гарантирована. Если найдется вариант, где xy меньше, чем вес s-w, то мы сможем перехитрить систему. Предположим, что вес w-s равен z, и xyz > 1, тогда цикл s-t-w-s позволяет конвертировать одну единицу валюты s в более чем одну единицу (xyz) валюты s. То есть можно получить доход в 100(xyz - 1) процентов, конвертировав s в t, затем в w и снова в s. Данная ситуация является примером арбитражных операций (arbitrage), которые позволили бы нам получать безграничные доходы, если бы не существовало сил вне модели - как, например, ограничения на размер сделок. Чтобы преобразовать эту задачу в задачу поиска кратчайших путей, прологарифмируем все числа так, чтобы веса путей соответствовали сумме весов ребер вместо их умножения, а затем изменим их знаки, чтобы обратить неравенства. При этом веса ребер могут оказаться отрицательными или положительными, а кратчайший путь из s в t дает наилучший способ конвертации валюты s в валюту t. Цикл с наименьшим весом указывает лучшую возможность для арбитражных операций, хотя выгоден любой отрицательный цикл.
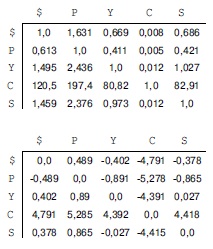
Таблица в верхней части содержит переводные коэффициенты одной валюты в другую. Например, второй элемент в верхнем ряду означает, что за 1 доллар можно купить 1,631 единиц валюты P. Конвертация $1000 в валюту P и обратно должна дать $1000*1,631*0,613 = $999, т.е. потеря составляет $1. Однако конвертация $1000 в валюту P, затем в валюту Yи обратно в доллары дает $1000*1,631*0,411*1,495 = $1002 , т.е. прибыль 0,2%. Если составить новую таблицу (внизу) из отрицательных логарифмов всех чисел, то ее можно считать матрицей смежности для полной сети с весами ребер, которые могут быть как положительными, так и отрицательными. В этой сети узлы соответствуют валютам, ребра - конвертациям, а пути - последовательностям конвертаций. Описанная конверсия соответствует циклу $-P-Y-$ в графе с весом -0,489 + 0,890 - 0,402 = -0,002. Лучшая возможность для арбитражных операций соответствует наиболее короткому циклу в графе.
Можно ли обнаружить в сети отрицательные циклы или найти кратчайшие пути в сетях, которые не содержат отрицательных циклов? Существование эффективных алгоритмов для решения этих задач не противоречит NP-трудности общей задачи, которая была доказана в лемме 21.18, поскольку сведение задачи поиска гамильтонова пути к любой из этих задач не известно. А именно, сведение леммы 21.18 говорит о том, чего мы не можем сделать: создать алгоритм, который может гарантированно и эффективно найти путь с наименьшим весом в любой заданной сети, если в ней допускаются отрицательные веса ребер. Такая постановка задачи представляется слишком общей. Однако можно решить ограниченные версии этой задачи, хотя это и не так легко, как для других ограниченных версий данной задачи (положительные веса и ациклические сети), которые мы изучили выше в этой главе.
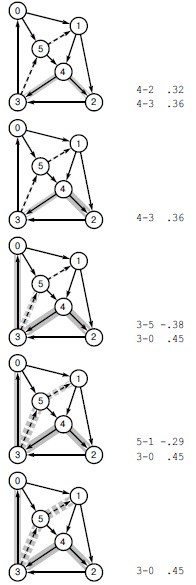
В общем случае, как было сказано в разделе 21.2, алгоритм Дейкстры не работает при наличии отрицательных весов, даже если ограничиться рассмотрением сетей, в которых нет отрицательных циклов. На рис. 21.28 продемонстрировано это утверждение. Основное затруднение состоит в том, что в этом алгоритме пути рассматриваются в порядке возрастания их длины. Доказательство правильности алгоритма (см. лемму 21.2) предполагает, что добавление ребра к пути делает этот путь более длинным.
В этом примере алгоритм Дейкстры решает, что кратчайшим путем из 4 в 2 является путь 4-2 (длиной 0.32), и упускает более короткий путь 4-3-5-1-2 (длиной 0.20).
Алгоритм Флойда (Floyd) не нуждается в таком предположении и эффективен даже тогда, когда веса ребер могут быть отрицательными. Если нет отрицательных циклов, он вычисляет кратчайшие пути; примечательно, что в случае существования отрицательных циклов этот аглоритм обнаруживает по крайней мере один из них.
Лемма 21.20. Алгоритм Флойда ( рис. 21.29) решает задачу обнаружения отрицательного цикла и задачу поиска кратчайших путей для всех пар вершин в сетях, которые содержат отрицательные циклы, за время, пропорциональное V3.
Доказательство. Доказательство леммы 21.8 не зависит от того, могут ли веса ребер быть отрицательными, однако при наличии ребер с отрицательными весами нужна другая интерпретация результатов. Каждый элемент в матрице свидетельствует о том, что алгоритм обнаружил путь этой длины. В частности, любой отрицательный элемент на диагонали матрицы расстояний означает наличие по крайней мере одного отрицательного цикла. При наличии отрицательных циклов мы не можем непосредственно делать какие-либо дальнейшие выводы, т.к. пути, которые алгоритм неявно проверяет, не обязательно просты: ведь некоторые из них могут содержать один и более витков по одному отрицательному циклу или нескольким. Однако если отрицательных циклов нет, то пути, которые вычисляются алгоритмом, просты, поскольку любой путь с циклом означает существование такого пути, который соединяет те же две точки, но содержит меньше ребер и имеет не больший вес (тот же путь с удаленным циклом). 
Доказательство леммы 21.20 не дает конкретного рецепта, как найти конкретный отрицательный цикл, исходя из матриц расстояний и путей, вычисляемых по алгоритму Флойда. Мы оставляем это задание в качестве самостоятельного упражнения (см. упражнение 21.122).
Алгоритм Флойда решает задачу поиска кратчайших путей для всех пар вершин в графах, которые не содержат отрицательных циклов (см. рис. 21.29). Учитывая отказ алгоритма Дейкстры в сетях, которые могут содержать отрицательные веса, алгоритм Флойда позволяет решить задачу для всех пар вершин в разреженных сетях без отрицательных циклов за время, пропорциональное V3. Если в таких сетях нужно решить задачу с одним истоком, можно применить это решение сложности V3 для всех пар вершин. Хотя при этом выполняется много лишней работы, это лучшее, что мы пока знаем для задачи с одним истоком. Можно ли разработать более быстрые алгоритмы для этих задач - такие, время выполнения которых сравнимо с алгоритмом Дейкстры для положительных весов ребер (E lg V для кратчайших путей из одного истока и VE lg V для кратчайших путей для всех пар вершин)? Мы можем ответить утвердительно на этот вопрос в отношении задачи для всех пар вершин; и можно снизить трудоемкость в худшем случае до VE для задачи с одним истоком.
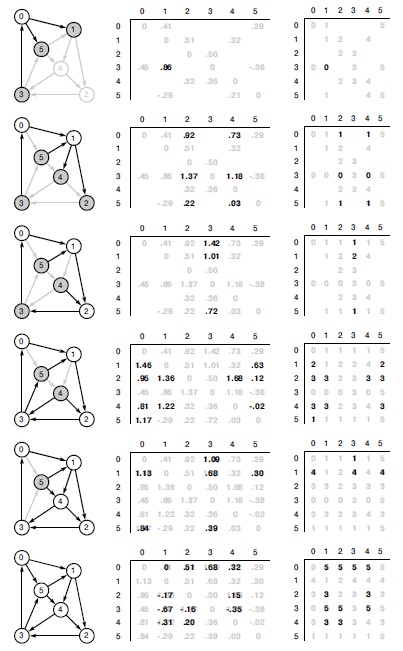
Эта последовательность демонстрирует построение матриц всех кратчайших путей для орграфа с отрицательными весами с помощью алгоритма Флойда. Первый шаг совпадает с приведенным на рис. 21.14. На втором шаге в игру вступает отрицательное ребро 5-1, и находятся пути 5-1-2 и 5-1-4. Алгоритм выполняет точно такую же последовательность шагов релаксации для любых весов, однако результаты отличаются.
А вот вопрос преодоления барьера VE для общей задачи поиска кратчайших путей из одного истока является по-прежнему открытым.
Следующий подход, разработанный Р. Беллманом (R. Bellman) и Л. Фордом (L. Ford) в конце 1950-х годов, предоставляет простую и эффективную основу для решения задач поиска кратчайших путей из одного истока в сетях без отрицательных циклов. Чтобы вычислить кратчайшие пути из вершины s, мы (как обычно) используем индексированный именами вершин вектор wt, такой, что wt[t] содержит длину кратчайшего пути из s в t. В wt[s] заносим 0, а во все другие элементы wt - большое сигнальное значение, после чего вычисляем кратчайшие пути следующим образом:
Просматриваем ребра сети в любом порядке и выполняем релаксацию вдоль каждого ребра. Выполняем V таких действий.
Общий метод выполнения V проходов по ребрам с просмотром ребер в любом порядке мы будем называть алгоритмом Беллмана-Форда (Bellman-Ford). Некоторые авторы применяют этот термин для описания еще более общего метода (см. упражнение 21.130).
Например, для графа, представленного списками смежности, алгоритм Беллмана-Форда поиска кратчайших путей из начальной вершины s можно реализовать так. Сначала занесем в элементы wt значения, большие, чем любая длина пути, а в элементы spt - пустые указатели, и затем выполним следующий код:
wt[s] = 0;
for (i = 0; i < G->V(); i++)
for (v = 0; v < G->V(); v++)
{ if (v != s && spt[v] == 0) continue;
typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
if (wt[e->w()] > wt[v] + e->wt())
{ wt[e->w()] = wt[v] + e->wt(); st[e->w()] = e; }
}
Этот код демонстрирует простоту базового метода. Однако на практике он не используется: как вскоре будет показано, его простые модификации дают реализации, которые более эффективны для большинства графов.