|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Кратчайшие пути
Сведение
Задачи о кратчайших путях - особенно общий случай, где допустимы отрицательные веса (тема раздела 21.7) - представляют обобщенную математическую модель, которую можно использовать для решения множества других задач, с виду не имеющих отношения к обработке графов. Эта модель является первой среди ряда таких общих моделей, с которыми мы еще встретимся. По мере перехода к более трудным задачам и все более общим моделям возникает одна из сложностей - точное описание взаимосвязей между различными задачами. Для каждой новой задачи требуется ответить на вопрос: возможно ли ее простое решение с помощью преобразования в задачу, которую мы уже умеем решать? Станет ли решение более легким, если наложить на задачу некоторые ограничения? Чтобы отвечать на подобные вопросы, в этом разделе мы ненадолго отклонимся от темы и обсудим термины, используемые для описания таких видов взаимосвязи между задачами.
Определение 21.3. Мы говорим, что некоторая задача A сводится к (reduces to) другой задаче B, если алгоритм решения задачи B можно использовать для разработки алгоритма решения задачи A с общим временем выполнения в худшем случае, которое не более чем в постоянное число раз превышает выполнения алгоритма решения задачи B в худшем случае. Мы говорим, что две задачи эквивалентны, если они сводятся одна к другой.
Отложим до части VIII строгое определение того, что означают слова " использовать" один алгоритм для " разработки " другого. Для большинства приложений достаточно следующего простого приема. Мы показываем, что A сводится к B, если покажем возможность решения любого экземпляра задачи A за три шага:
- Преобразование ее к задаче B.
- Решение полученной задачи B.
- Преобразование решения задачи B в решение задачи A.
Если мы сможем эффективно выполнить эти преобразования (и решить задачу B), то мы сможем эффективно решить и задачу A. Для демонстрации такой методики доказательства рассмотрим два примера.
Лемма 21.12. Задача транзитивного замыкания сводится к задаче поиска кратчайших путей для всех пар вершин с неотрицательными весами.
Доказательство. Мы уже отмечали прямую связь между алгоритмами Уоршалла и Флойда. Возможен другой способ установить их взаимосвязь в настоящем контексте: представьте, что требуется вычислить транзитивное замыкание орграфов с помощью библиотечной функции поиска всех кратчайших путей в сетях. Для этого мы добавим в орграф петли, если их нет, а затем построим сеть непосредственно из матрицы смежности орграфа с произвольным весом (скажем, 0.1), соответствующим каждому единичному элементу и сигнальным весом, соответствующим каждому нулевому элементу. Затем вызовем функцию поиска кратчайших путей для всех пар вершин. Из вычисленной матрицы кратчайших путей для всех пар вершин можно легко найти транзитивное замыкание: для любых двух заданных вершин u и v путь в орграфе из u в v существует тогда и только тогда, когда длина пути в сети из u в v не равна нулю (см.
рис.
21.21). 
Матрицу смежности (с петлями) заданного орграфа (слева) можно преобразовать в матрицу смежности, представляющую сеть, присвоив каждому ребру произвольный вес (матрица слева). Как обычно, пустые элементы матрицы означают сигнальные значения, указывающие на отсутствие ребра. Если имеется матрица длин кратчайших путей для всех пар вершин этой сети (матрица в центре), то транзитивное замыкание орграфа (матрица справа) - это просто матрица, образованная заменой сигнальных значений на 0, а всех других элементов на 1.
Эта лемма является формальным утверждением, что задача транзитивного замыкания является не более трудной, чем задача кратчайших путей для всех пар вершин. Поскольку мы знакомы с алгоритмами транзитивного замыкания, которые работают даже быстрее, чем известные нам алгоритмы для задач поиска кратчайших путей для всех пар вершин, это утверждение не удивляет. Сведение представляет интерес тогда, когда оно используется для установки взаимосвязи между задачами, решение которых нам не известно, или между такими задачами и задачами, которые мы умеем решать.
Лемма 21.13. В сетях без ограничений на веса ребер задачи поиска наиболее длинного пути и кратчайшего пути (из одного истока или для всех пар вершин) эквивалентны.
Доказательство. Для заданной задачи поиска кратчайшего пути изменим знаки всех весов. Наиболее длинный (т.е. с наибольшим весом) путь в модифицированной сети является кратчайшим путем в исходной сети. Аналогичное рассуждение показывает, что задача поиска кратчайшего пути сводится к задаче поиска наиболее длинного пути. 
Это доказательство тривиально, но данная лемма также показывает, что при утверждении и доказательстве сведения нужно быть аккуратным, поскольку легко посчитать сведение само собой разумеющимся, когда это не так. Например, утверждение, что задачи о наиболее длинном и кратчайшем пути эквивалентны в сетях с неотрицательными весами, не соответствует действительности.
В начале этой главы было схематично показано, что задача поиска кратчайших путей в неориентированных взвешенных графах сводится к задаче нахождения кратчайших путей в сетях, поэтому наши алгоритмы для сетей можно использовать для решения задач поиска кратчайших путей в неориентированных взвешенных графах. В этом контексте стоит рассмотреть два дополнительных момента, касающихся сведения. Во-первых, обратное утверждение неверно: умение находить кратчайшие пути в неориентированных взвешенных графах не поможет находить их в сетях. Во-вторых, мы уже видели неточность в рассуждении: если веса ребер могут быть отрицательными, сведение приведет к сети с отрицательными циклами, а мы не умеем находить в них кратчайшие пути. Но даже если сведение не помогает, все-таки можно найти кратчайшие пути в неориентированных взвешенных графах без отрицательных циклов с помощью неожиданно сложного алгоритма (см. раздел ссылок). Поскольку эта задача не сводится к ориентированному варианту, данный алгоритм бесполезен при решении задачи поиска кратчайшего пути в сетях общего вида.
По существу, концепция сведения описывает процесс использования одного АТД для реализации другого, как это обычно делается современными системными программистами. Если две задачи эквивалентны, и мы умеем эффективно решать какую-то из них, мы можем эффективно решить и другую. Мы часто находим простые взаимно однозначные соответствия, как, например, в лемме 21.13, где показана эквивалентность двух задач. В этом случае, даже до обсуждения способа решения каждой из задач, важно знать, что если удастся найти эффективное решение одной задачи, то его можно применить и для решения другой. Еще один пример был приведен в "Виды графов и их свойства" : когда мы рассматривали задачу определения, содержит ли граф нечетный цикл, мы установили, что эта задача эквивалентна определению, можно ли раскрасить граф двумя цветами.
Сведение имеет два основных применения в проектировании и анализе алгоритмов. Во-первых, оно помогает классифицировать задачи по их сложности на соответствующем абстрактном уровне, без разработки и анализа полных реализаций. Во-вторых, сведение часто помогает установить нижние границы трудности решения различных задач, чтобы знать, где следует прекращать поиск лучших алгоритмов. Мы видели примеры такого применения в "Орграфы и DAG-графы" и "Минимальные остовные деревья" ; другие примеры будут приведены ниже в этом разделе.
Помимо такой непосредственной практической пользы, принцип сведения также широко применяется в теории вычислений. Эти результаты важны потому, что позволяют обрести понимание при решении все более трудных задач. Данная тема будет кратко рассмотрена в конце настоящего раздела и во всех подробностях - в части VIII.
Естественно, трудоемкость преобразований обычно не должна быть больше трудоемкости решения. Однако во многих случаях сведение можно использовать даже при доминировании стоимости преобразования. Одно из наиболее важных применений сведения заключается в преобразовании к уже изученной задаче, для которой известно эффективное решение, что обеспечивает эффективные решения таких задач, которые иначе считались бы трудноразрешимыми. Сведение A к B, даже если это преобразование обойдется намного дороже, чем решение B, может дать намного более эффективный алгоритм решения, чем созданные другими способами. Существует множество различных вариантов. Возможно, нам более важна ожидаемая трудоемкость, а не трудоемкость в худшем случае. Возможно, для решения A потребуется решить две задачи, B и C. Может быть, потребуется многократно решить задачу B. Мы отложим дальнейшее обсуждение таких вариаций до части 8, поскольку все примеры, которые мы будем рассматривать до этого, не сложнее только что рассмотренных.
В частности, когда мы решаем задачу A, упрощая другую задачу B, мы знаем, что A сводится к B, но не обязательно наоборот. Например, выборка сводится к сортировке, поскольку наименьший k-й элемент в файле можно найти, отсортировав файл и затем перейдя по индексу (или последовательно) в его k-ю позицию; однако отсюда, конечно же, не следует, что сортировка сводится к выборке. В данном контексте и задача поиска кратчайших путей для взвешенного DAG, и задача поиска кратчайших путей для сетей с положительными весами сводится к общей задаче вычисления кратчайших путей. Такое использование сведения соответствует естественному пониманию, что одна задача является более общим случаем, чем другая. Любой алгоритм сортировки решает любую задачу выборки и, если мы можем решить задачу поиска кратчайших путей в сетях общего вида, то, конечно, можно воспользоваться этим решением для сетей с различными ограничениями. Однако обратное утверждение не обязательно верно.
Такое применение сведения удобно, однако эта концепция более полезна, если использовать ее для получения информации о взаимосвязях между задачами из различных областей. Например, рассмотрим следующие задачи, которые на первый взгляд кажутся далекими от обработки графов. Сведение помогает выявить определенные взаимоотношения между этими задачами и задачей поиска кратчайших путей.
Календарное планирование. Пусть необходимо выполнить большой набор работ разной продолжительности. Мы можем одновременно выполнять любое количество работ, однако существует множество отношений предшествования в виде пар работ, которые указывают, какая из работ должна быть завершена до начала выполнения другой работы. Каково минимальное время, которое необходимо для завершения всех работ, при условии выполнения всех ограничений предшествования? Конкретнее, для данного множества работ (с их длительностями) и множества ограничений предшествования требуется составить такой график их выполнения (найти момент начала для каждой работы), который позволяет достичь этого минимума.
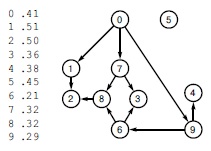
На рис. 21.22 приведен пример задачи календарного планирования. Здесь используется естественное представление в виде сети, которое в данном случае послужит инструментом сведения. Этот вариант задачи является, возможно, наиболее простым из буквально сотен изученных вариантов, которые содержат другие характеристики работ и другие ограничения - например, назначение работам персонала или других ресурсов, других расходов, конечных сроков выполнения и т.п. В этом контексте описанный выше вариант обычно называется календарным планированием с ограничениями предшествования и неограниченным параллелизмом. Для краткости в дальнейшем мы будем применять термин календарное планирование.
Для упрощения разработки алгоритма, решающего задачу планирования работ, мы рассмотрим следующую задачу, которая представляет интерес и сама по себе.
В этой сети вершины представляют работы, которые требуется выполнить (с весами, указывающими необходимое время), а ребра - отношения предшествования между работами. Например, ребра из 7 в 8 и в 3 означают, что работа 7 должна быть завершена до начала работы 8 и работы 3. Каково минимальное время, необходимое для завершения всех работ?
Разностные ограничения. Нужно присвоить неотрицательные значения множеству переменных x0, ..., xn , которые минимизируют значение xn, удовлетворяя множеству разностных ограничений на переменные, каждое из которых указывает, что разность между какими-то двумя переменными должна быть больше или равна заданной константе.
На рис. 21.23 показан пример такой задачи. Это исключительно абстрактная математическая формулировка, которая может служить основой для решения многих практических задач (см. раздел ссылок).
Задача разностных ограничений является частным случаем гораздо более общей задачи, где в выражениях допускаются произвольные линейные комбинации переменных.
Линейное программирование. Нужно присвоить неотрицательные значения множеству переменных x0, ..., xn , которые минимизируют значение заданной линейной комбинации переменных при наличии множества ограничений на переменные, каждое из которых указывает, что заданная линейная комбинация переменных должна быть больше или равна некоторой заданной константе.
Линейное программирование является широко распространенным общим способом решения широкого класса задач оптимизации, подробное обсуждение которых мы отложим до части VIII. Очевидно, что, как и многие другие задачи, задача разностных ограничений сводится к линейному программированию. В данный момент нас интересует взаимосвязь между разностными ограничениями, календарным планированием и задачами поиска кратчайших путей.