|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Кратчайшие пути
Основные принципы
Наши алгоритмы поиска кратчайших путей основаны на простой операции, которая называется релаксация (relaxation). В начале работы алгоритма поиска кратчайших путей известны только ребра сети и их веса. По мере продвижения мы собираем сведения о кратчайших путях, которые соединяют различные пары вершин. Все наши алгоритмы пошагово обновляют эти сведения и делают новые выводы о кратчайших путях на основе информации, полученной к текущему моменту. На каждом шаге мы проверяем, можно ли найти путь, более короткий, чем некоторый известный путь. Термин " релаксация " (ослабление) обычно относится к этому шагу, который ослабляет ограничения на кратчайший путь. Представьте себе резиновую ленту, плотно натянутую на путь, соединяющий две вершины: успешная операция релаксации позволяет ослабить натяжение этой резиновой ленты вдоль более короткого пути.
Наши алгоритмы основываются на многократном применении одной из двух операций релаксации:
- Релаксация ребра. Проверка, дает ли продвижение по данному ребру новый кратчайший путь к конечной вершине.
- Релаксация пути. Проверка, дает ли прохождение через данную вершину новый кратчайший путь, соединяющий две другие заданных вершины.
Релаксация ребра представляет собой частный случай релаксации пути; однако мы рассматриваем эти операции по отдельности, поскольку используем их по отдельности (первая операция - в алгоритмах для одного истока, а вторая - в алгоритмах для всех пар вершин). В обоих случаях главное требование к структурам данных, которые используются для представления текущего состояния знаний о кратчайших путях сети, состоит в том, чтобы можно было легко обновлять их - для отображения изменений, выполненных операцией релаксации.
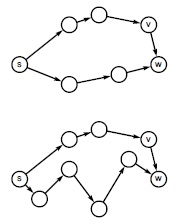
Здесь показана операция релаксации, лежащая в основе наших алгоритмов поиска кратчайших путей из одного истока. Мы прослеживаем известные кратчайшие пути из истока s в каждую вершину и проверяем, образует ли ребро v-w более короткий путь в w. В верхнем примере это не так, поэтому ребро игнорируется. В нижнем примере получается более короткий путь - значит, нужно обновить структуры данных, чтобы указать, что лучший известный путь из s в w проходит через v, завершаясь ребром v-w.
Сначала рассмотрим релаксацию ребра (см. рис. 21.5). Все рассматриваемые нами алгоритмы поиска кратчайших путей из одного истока основаны на следующем шаге: приводит ли данное ребро к рассмотрению более короткого пути из истока к конечной вершине этого ребра?
Структуры данных, необходимые для выполнения этих действий, просты. Во-первых, наша основная задача состоит в вычислении длины кратчайших путей из истока в каждую из прочих вершин. Условимся сохранять длины известных кратчайших путей из истока в каждую из вершин в векторе wt, индексированном именами вершин. Во-вторых, для записи самих путей продвижения от вершины к вершине мы будем придерживаться того же соглашения, что и в других алгоритмах поиска на графах в лекциях 18-20: мы используем индексированный именами вершин вектор spt для записи последнего ребра на кратчайшем пути из истока в данную индексированную вершину. Эти ребра составляют дерево.
Теперь реализация релаксации ребра выполняется просто.
При поиске кратчайших путей из одного истока следующий код выполняет релаксацию вдоль ребра e, направленного от v к w:
if (wt[w] > wt[v] + e->wt())
{ wt[w] = wt[v] + e->wt(); spt[w] = e; }
Этот кодовый фрагмент и прост, и выразителен; и мы включаем его в наши реализации, не определяя релаксацию в виде высокоуровневой абстрактной операции,.
Определение 21.2. Пусть задана сеть и некоторая вершина s. Деревом кратчайших путей (Shortest-Paths Tree - SPT) для s является подсеть, содержащая s и все вершины, достижимые из s, которая образует такое направленное дерево с корнем в s, что каждый путь в дереве является кратчайшим путем в сети.
Возможно существование нескольких путей одной и той же длины, соединяющих заданную пару узлов, так что SPT-деревья не обязательно уникальны. Вообще, как видно из рис. 21.2, если выбрать кратчайшие пути из вершины s в каждую вершину, достижимую из s в сети, и из подсети, порожденной ребрами этих путей, то можно получить DAG. Различные кратчайшие пути, соединяющие пары узлов, могут рассматриваться как подпути некоторого более длинного пути, содержащего оба узла. Поэтому мы обычно ограничиваемся вычислением любого SPT для данного орграфа и начальной вершины.
Элементы вектора wt в наших алгоритмах обычно инициализируются сигнальным значением. Это значение должно быть достаточно малым, чтобы его добавление при проверке релаксации не привело к переполнению, но достаточно большим, чтобы никакой простой путь не имел больший вес. Например, если веса ребер находятся между 0 и 1, то в качестве сигнального значения можно выбрать V. Когда сигнальные значения используются в сетях, где могут быть отрицательные веса, следует очень тщательно проверить наши допущения. Например, если обе вершины имеют сигнальные значения, то вышеприведенный код релаксации не выполнит никаких действий, если e.wt не отрицательно (как обычно и бывает в большинстве реализаций), однако изменит wt[w] и spt[w], если этот вес отрицателен.
В качестве индекса для сохранения ребер SPT (spt[w]->w() == w) наш код всегда использует конечную вершину. Для краткости и согласованности с главами 17-19 мы применяем для ссылки на вершину spt[w]->v() обозначение st[w] (в тексте и особенно на рисунках), чтобы подчеркнуть, что вектор spt на самом деле является представлением родительскими ссылками дерева кратчайших путей (см. рис. 21.6). Для вычисления кратчайшего пути из s в t нужно подняться по дереву от t к s; при этом мы проходим по ребрам в направлении, противоположном их ориентации в сети, и посещаем вершины пути в обратном порядке (t, st[t], st[st[t]] и т.д.).
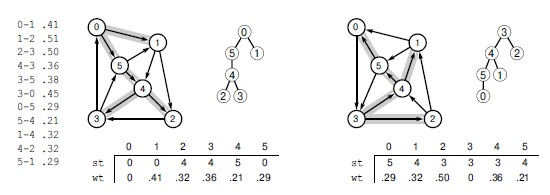
Кратчайшие пути из 0 к другим узлам в этой сети - это, соответственно, 0-1, 0-5-4-2, 0-5-4-3, 0-5-4 и 0-5. Эти пути определяют остовное дерево, которое приведено в центре в трех представлениях: серые ребра в графическом изображении сети, ориентированное дерево и родительские ссылки с весами. Ссылки в представлении родительскими ссылками (которое мы обычно вычисляем), ориентированы противоположно ссылкам в орграфе, поэтому мы иногда работаем с обратным орграфом. Остовное дерево, определяемое кратчайшими путями из 3 в каждый из других узлов в обращении сети, показано справа. Представление этого дерева родительскими ссылками дает кратчайшие пути из каждого из других узлов в узел 2 в исходном графе. Например, кратчайший путь 0-5-4-3 из 0 в 3 можно найти, пройдя по ссылкам st[0] = 5, st[5] = 4 и st[4] = 3.
Один из способов получения ребер пути из SPT в прямом порядке (от истока к стоку) использует стек. Например, следующий код выводит путь из истока в заданную вершину w:
stack <EDGE *> P; EDGE *e = spt[w];
while (e) { P.push(e); e = spt[e->v()]); }
if (P.empty()) cout << P.top()->v();
while (!P.empty())
{ cout << "-" << P.top()->w(); P.pop(); }
В реализации класса можно использовать аналогичный код, чтобы клиент получил вектор, содержащий ребра пути.
Если необходимо просто вывести или как-то по-другому обработать ребра пути, проход по всему пути в обратном порядке для достижения первого ребра может оказаться нежелательным. Один из способов обхода этого затруднения - работа с обратной сетью, как показано на рис. 21.6. В задачах с одним истоком мы используем обратный порядок и релаксацию ребер, поскольку SPT дает компактное представление кратчайших путей из истока во все другие вершины в векторе, который содержит лишь V элементов.
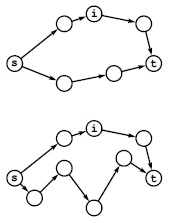
Здесь продемонстрирована операция релаксации, на которой основаны наши алгоритмы поиска кратчайших путей для всех пар вершин. Мы отслеживаем лучший известный путь между всеми парами вершин и проверяем, может ли вершина i улучшить путь из s в t. В верхнем примере это не так, а в нижнем путь можно улучшить. Когда встречается такая вершина i, что сумма длины известного кратчайшего пути из s в i и длины известного кратчайшего пути из i в t меньше длины известного кратчайшего пути из s в t, мы обновляем наши структуры данных, чтобы указать, что теперь известен более короткий путь из s в t (в направлении к i).
Теперь мы рассмотрим релаксацию пути - основу некоторых наших алгоритмов для всех пар вершин: дает ли прохождение через данную вершину более короткий путь, соединяющий две другие заданные вершины? Например, предположим, что имеются три вершины s, x и t, и нужно узнать, что лучше: пройти из s в x, а затем из x в t, или сразу пройти из s в t, не заходя в x. Для прямолинейных соединений в евклидовом пространстве неравенство треугольника утверждает, что маршрут через x не может быть более коротким, чем прямой маршрут из s в t, но для путей в сети это вполне возможно (см. рис. 21.7). Чтобы определить, как именно обстоят дела, необходимо знать длины путей из s в x, из x в t и из s в t (без захода в x). Затем мы просто проверяем, меньше ли сумма длин первых двух путей, чем длина третьего; если это так, нужно соответствующим образом обновить данные.
Релаксация пути входит в решение задачи для всех пар вершин, где мы храним длины найденных на данный момент кратчайших путей между всеми парами вершин. А именно, в коде вычисления кратчайших путей для всех пар вершин мы используем вектор векторов d - такой, что значение d[s][t] содержит длину кратчайшего пути из s в t, и вектор векторов p - такой, что p[s][t] содержит следующую вершину на кратчайшем пути из s в t. Первый вектор называется матрицей расстояний, а второй - матрицей путей.
На рис. 21.8 показаны эти матрицы для нашей демонстрационной сети. Главной целью вычислений является матрица расстояний, а матрица путей используется потому, что она явно более компактна, хотя и содержит ту же информацию, что и полный список путей, приведенный на рис. 21.3.
Две матрицы справа - компактные представления всех кратчайших путей для демонстрационной сети, приведенной слева. Они содержат ту же информацию, что и список на рис. 21.3. Матрица расстояний слева содержит длины кратчайших путей: значение элемента на пересечении строки s и столбца t равно длине кратчайшего пути из s в t. Матрица путей справа содержит информацию, необходимую для обхода пути: элемент на пересечении строки s и столбца t содержит следующую вершину на пути из s в t.
При наличии этих структур данных релаксация пути выражается следующим кодом:
if (d[s][t] > d[s][x] + d[x][t])
{ d[s][t] = d[s][x] + d[x][t]; p[s][t] = p[s][x]; }
Как и в случае релаксации ребра, этот код можно считать точной записью данного выше неформального описания, и мы вставляем его непосредственно в наши реализации. А более формально релаксация пути отражает следующее.
Лемма 21.1. Если вершина x лежит на кратчайшем пути из s в t, то этот путь состоит из кратчайшего пути из s в x, за которым следует кратчайший путь из x в t.
Доказательство. Если бы это было не так, мы могли бы воспользоваться любым более коротким путем из s в x или из x в t для построения более короткого пути из s в t. 
Мы сталкивались с операцией релаксации пути при рассмотрении алгоритмов транзитивного замыкания в "Орграфы и DAG-графы" . Если веса ребер и путей либо равны 1, либо бесконечны (т.е. вес пути равен 1 только если все его ребра имеют единичный вес), то релаксация пути - это операция, которая использовалась в алгоритме Уоршалла (если существуют пути из s в x и из x в t, то существует и путь из s в t). Если определить вес пути как количество ребер в этом пути, то алгоритм Уоршалла обобщает алгоритм Флойда для нахождения всех кратчайших путей в невзвешенном орграфе. Как будет показано в разделе 21.3, его можно обобщить еще дальше - применительно к сетям.
С математической точки зрения важно, что все эти алгоритмы можно привести к унифицированному алгебраическому виду, который помогает их пониманию. С точки зрения программиста важно, что каждый из этих алгоритмов можно реализовать, используя абстрактную операцию + (для вычисления веса пути из весов ребер) и абстрактную операцию < (для вычисления минимального значения из множества весов путей) - исключительно в контексте операции релаксации (см. упражнения 19.55 и 19.56).
Из леммы 21.1 следует, что кратчайший путь из s в t содержит кратчайшие пути из s в каждую другую вершину на пути в t. Большинство алгоритмов поиска кратчайших путей также вычисляют кратчайшие пути из s в каждую вершину, которая находится ближе к s, чем к t (независимо от того, находится ли эта вершина на пути из s в t), хотя это и не обязательно (см. упражнение 21.8). Решение задачи о кратчайших путях из истока в сток с помощью такого алгоритма, когда t является наиболее удаленной от s вершиной, эквивалентно решению задачи о кратчайших путях из одного истока s. И наоборот, решение задачи о кратчайших путях из одного истока s можно использовать для нахождения вершины, наиболее удаленной от s.
Матрица путей, применяемая в наших реализациях задачи для всех пар вершин, является также представлением деревьев кратчайших путей для каждой вершины. Мы определили p[s][t] как вершину, которая следует за s на кратчайшем пути из s в t. Ну или как вершину, которая в обратной сети предшествует s на кратчайшем пути из t в s. Другими словами, столбцом t в матрице путей сети является индексированный именами вершин вектор, который в обращении сети представляет SPT для вершины t. И наоборот, можно построить матрицу путей для сети, заполнив каждый столбец деревом кратчайших путей, которое представлено индексированным именами вершин вектором для соответствующей вершины в обращении сети. Это соответствие показано на рис. 21.9.
Итак, релаксация предоставляет базовые абстрактные операции, необходимые для построения алгоритмов поиска кратчайших путей. Основная сложность здесь - выбор, указывать ли начальное или конечное ребро в кратчайшем пути. Например, алгоритмы для одного истока более естественно выражаются при задании пути конечным ребром: тогда для реконструкции пути потребуется только один индексированный именами вершин вектор, поскольку все пути ведут обратно к истоку. Этот выбор не представляет принципиальной трудности, поскольку можно либо использовать обратный граф, либо добавить функции-члены, которые скрывают разницу от клиентов. Например, в интерфейсе можно определить функцию-член, которая возвращает ребра кратчайшего пути в векторе (см. упражнения 21.15 и 21.16).
Поэтому для простоты все наши реализации в этой главе содержат функцию-член dist, которая возвращает длину кратчайшего пути и либо функцию-член path, возвращающую начальное ребро в кратчайшем пути, либо функцию-член pathR, которая возвращает конечное ребро в кратчайшем пути. К примеру, наши программы для одного истока, в которых применяется релаксация ребра, обычно реализуют эти функции так:
Edge *pathR(iirt w) const { return spt[w]; }
double dist(int v) { return wt[v]; }
Аналогично, реализации поиска всех путей, которые используют релаксацию пути, обычно реализуют эти функции так:
Edge *path(int s, int t) { return p[s][t]; }
double dist(int s, int t) { return d[s][t]; }
В некоторых ситуациях стоило бы построить интерфейсы, стандартизующие один, или другой, или оба этих варианта, но мы будем выбирать для каждого конкретного алгоритма наиболее естественный вариант.
Здесь показаны SPT-деревья для каждой вершины в обращении сети с рис. 21.8 (от 0 до 5, сверху вниз): в виде поддеревьев сети (слева), ориентированных деревьев (в центре) и представления родительскими ссылками, вместе с индексированным именами вершин массивом длин путей (справа). Объединение этих массивов формирует матрицы путей и расстояний (где каждый массив становится столбцом) и дает решение задачи о кратчайших путях для всех пар вершин, которая показана на рис. 21.8.
Упражнения
21.12. Нарисуйте SPT из вершины 0 для сети, определенной в упражнении 21.1, и для ее обращения. Приведите представление родительскими ссылками для обоих деревьев.
21.13. Считайте ребра в сети, определенной в упражнении 21.1, неориентированными ребрами - когда каждому ребру в сети соответствуют два разнонаправленных ребра равного веса. Выполните упражнение 21.12 для этой сети.
21.14. Измените на рис. 21.2 направление ребра 0-3. Нарисуйте два различных SPT с корнем в вершине 2 для этой измененной сети.
21.15. Напишите функцию, которая использует функцию-член pathR из реализации задачи для одного истока и помещает в контейнер vector из библиотеки STL указатели на ребра пути из истока v в заданную вершину w.
21.16. Напишите функцию, которая использует функцию-член path из реализации задачи для всех путей и помещает в контейнер vector из библиотеки STL указатели на ребра пути из заданной вершины v в другую заданную вершину w.
21.17. Напишите программу, которая использует функцию из упражнения 21.16 для вывода всех путей в стиле рис. 21.3.
21.18. Приведите пример, который показывает, как можно найти кратчайший путь из s в t, не зная длину более короткого пути из s в х для некоторого х.