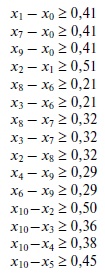НОУ ИНТУИТ | Алгоритмы на С++. Лекция 21: Кратчайшие пути

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.01.2015 | Доступ: свободный | Студентов: 2178 / 0 | Длительность: 63:16:00

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор, Тестировщик, Архитектор программного обеспечения

|

Вам нравится? Нравится 82 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лемма 21.14. Задача календарного планирования сводится к задаче разностных ограничений.

Доказательство. Для каждой работы добавим фиктивную работу и такое ограничение предшествования, что данная работа должна закончиться до начала фиктивной работы. Для этой задачи календарного планирования определим систему разностных неравенств, где каждой работе i соответствуют переменная x_i и ограничение, согласно которому работа j не может начаться до окончания работы i в соответствии с неравенством $x_{j} \geq x_{i}+c_{i}$ , где c_i, - продолжительность работы i. Решение задачи разностных ограничений дает как раз решение задачи календарного планирования, при этом значение каждой переменной задает время начала соответствующей работы. $\blacksquare$

На рис. 21.23 приведена система разностных неравенств, которая сформирована сведением задачи календарного планирования с рис. 21.22. Практическое значение этого сведения состоит в том, что для решения задачи календарного планирования можно воспользоваться любым алгоритмом, позволяющим решать задачи разностных ограничений.

Рис. 21.23. Разностные ограничения

Нахождение неотрицательных значений переменных, которые минимизируют значение x₁₀ с учетом данного множества неравенств, эквивалентно задаче календарного планирования работ, которая приведена на рис. 21.22. Например, неравенство $x_{8} \geq x_{7}+0,32$ означает, что работа 8 не может начаться до завершения работы 7.

Полезно подумать, можно ли провести аналогичное построение в обратном направлении: если имеется алгоритм решения задачи календарного планирования, то можно ли воспользоваться им для решения задачи разностных ограничений? Ответ на этот вопрос таков: формулировка леммы 21.14 не означает, что задача разностных ограничений сводится к задаче календарного планирования, поскольку системы разностных неравенств, которые получаются из задачи календарного планирования, имеют свойство, которое не обязательно справедливо для каждой задачи разностных ограничений. А именно: если в двух неравенствах совпадают вторые переменные, то совпадают и константы.

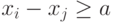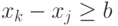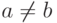Следовательно, алгоритм для календарного планирования работ непосредственно не позволяет решать системы разностных неравенств, если в них имеются два таких неравенства: $x_{i}-x_{j} \geq a$ и $x_{k}-x_{j} \geq b$ , где $a\neq b$ . При доказательстве возможности сведения следует иметь в виду ситуации, подобные следующей: в доказательстве, что A сводится к B, необходимо показать, что алгоритм решения задачи B позволяет решить любой вариант задачи A.

Константы в задачах разностных ограничений, создаваемые при доказательстве леммы 21.14, всегда неотрицательны. Этот факт имеет существенное значение.

Лемма 21.15. Задача разностных ограничений при положительных константах эквивалентна задаче поиска наиболее длинных путей из одного истока в ациклической сети.

Доказательство. Пусть задана система разностных неравенств. Построим сеть, где каждая переменная xt соответствует вершине i, а каждое неравенство 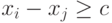$x_{i}-x_{j} \geq c$ соответствует ребру i-j веса с. Например, назначение каждому ребру в орграфе на рис. 21.22 веса его начальной вершины дает сеть, соответствующую множеству разностных неравенств с рис. 21.23 рис. 21.23. Добавим к сети фиктивную вершину с ребрами нулевого веса, направленными в каждую из остальных вершин. При наличии в сети цикла система разностных неравенств не имеет решения (поскольку из положительности весов следует, что значения переменных, соответствующих каждой вершине, строго уменьшаются при движении вдоль пути, и тогда наличие цикла означает, что некоторая переменная меньше себя самой), и остается сообщить об этом. Если же в сети нет циклов, мы решим задачу поиска наиболее длинных путей из одного истока - фиктивной вершины. Наиболее длинный путь существует для каждой вершины, т.к. сеть является ациклической (см. раздел 21.4). Присвоим каждой переменной длину наиболее длинного пути из фиктивной вершины в соответствующую вершину сети. Для каждой переменной существование этого пути означает, что значение такой переменной удовлетворяет ограничениям, но никакое меньшее значение ограничениям не удовлетворяет.

В отличие от доказательства леммы 21.14, данное доказательство можно расширить, чтобы показать эквивалентность двух задач, поскольку построение работает в обоих направлениях. Здесь нет ограничения, что два неравенства с одинаковыми вторыми переменными в неравенстве должны иметь одинаковые константы, и нет требования, что ребра, исходящие из любой заданной вершины в сети, должны иметь одинаковые веса. Для любой заданной ациклической сети с положительными весами такое же соответствие дает систему разностных ограничений с положительными константами, решение которой непосредственно дает решение задачи поиска наиболее длинных путей из одного истока в сети. Детали этого доказательства оставляем на самостоятельную проработку (см. упражнение 21.90). $\blacksquare$

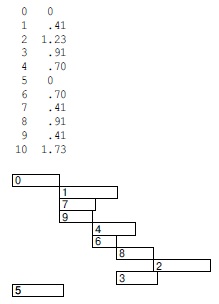
Сеть на рис. 21.22 демонстрирует это соответствие для нашей типовой задачи, а на рис. 21.15 показано вычисление наиболее длинных путей в сети с помощью программы 21.6 (фиктивная исходная вершина неявно фигурирует в реализации). График выполнения работ, вычисленный этим способом, приведен на рис. 21.24.

Программа 21.8 представляет собой реализацию, которая демонстрирует практическое применение данной теории. Она преобразовывает любую задачу календарного планирования в задачу поиска наиболее длинного пути в ациклических сетях, а затем использует программу 21.6 для ее решения.

Мы неявно предполагаем, что решение существует для любой постановки задачи календарного планирования работ; однако если во множестве ограничений предшествования имеется цикл, то невозможно составить расписание, удовлетворяющее таким ограничениям. Перед чем приступить к поиску наиболее длинных путей, следует проверить выполнение данного условия - для этого необходимо проверить, содержит ли соответствующая сеть цикл (см. упражнение 21.100). Поскольку подобная ситуация встречается часто, для ее описания обычно используется специальный технический термин.

Рис. 21.24. График выполнения работ

Этот рисунок демонстрирует решение задачи календарного планирования с рис. 21.22, полученное из соответствия между наиболее длинными путями во взвешенном DAG и календарным планированием. Длины наиболее длинных путей в массиве wt, вычисленном алгоритмом поиска наиболее длинных путей в программе 21.6 (см. рис. 21.15), в точности равны моментам времени начала работ (правый столбец вверху). Работы 0 и 5 начинаются в момент 0.00 , работы 1, 7 и 9 - в момент 0.41, работы 4 и 6 - в момент 0.70 и т.д.

Определение 21.4. Экземпляр задачи, для которого не существует решение, называется неразрешимым (infeasible).

Другими словами, для задач календарного планирования вопрос определения, является ли некоторый экземпляр задачи планирования разрешимым, сводится к задаче определения, является ли орграф ациклическим. По мере продвижения ко все более сложным задачам вопрос разрешимости становится все более важной (и все более трудной!) частью вычислительных затрат.

К данному моменту мы рассмотрели три взаимосвязанных задачи. Можно было бы просто показать, что задача планирования работ сводится к задаче поиска наиболее длинных путей из одного истока в ациклических сетях; однако мы также показали, что аналогично можно решить любую задачу разностных ограничений (с положительными константами) (см. упражнение 21.94), а также любую другую задачу, которая сводится к задаче разностных ограничений или задаче календарного планирования. Либо можно разработать алгоритм для решения задачи разностных ограничений и воспользоваться им для решения других задач, но мы не показали, что решение задачи календарного планирования может дать способ решения других задач.

Эти примеры демонстрируют использование сведения, которое позволяет расширить область применения проверенных реализаций. При построении реализаций в современном системном программировании подчеркивается необходимость многократного использования программного обеспечения с помощью разработки новых интерфейсов и использования существующих программных ресурсов. Этот важный процесс, который иногда называется библиотечным программированием (library programming), является практическим воплощением концепции сведения.

Библиотечное программирование чрезвычайно важно в практическом отношении, однако это не единственное применение сведения. Чтобы понять, что это значит, рассмотрим следующую версию задачи календарного планирования.

Календарное планирование с конечными сроками. В задаче планирования работ допускается дополнительный вид ограничений, которые определяют, что работа должна начаться до истечения заданного промежутка времени относительно другой работы. (Условные конечные сроки отсчитываются относительно начала всех работ.) Такие ограничения обычно требуются в критичных ко времени производственных процессах и во множестве других приложений; они могут существенно затруднить решение задачи календарного планирования.

Программа 21.8. Календарное планирование

Эта реализация читает из стандартного ввода список работ с их длительностями, за которым следует список ограничений предшествования, а затем выводит в стандартный вывод список моментов начала работ, которые удовлетворяют данным ограничениям. Используя леммы 21.14 и 21.15, а также программу 21.6, она решает задачу календарного планирования сведением ее к задаче поиска наиболее длинных путей для ациклических сетей.

  #include "GRAPHbasic.cc"
  #include "GRAPHio.cc"
  #include "LPTdag.cc"
  typedef WeightedEdge EDGE;
  typedef DenseGRAPH<EDGE> GRAPH;
  int main(int argc, char *argv[])
    { int i, s, t, N = atoi(argv[1]);
      double duration[N];
      GRAPH G(N, true);
      for (int i = 0; i < N; i++)
        cin >> duration[i];
      while (cin >> s >> t)
        G.insert(new EDGE(s, t, duration[s]));
      LPTdag<GRAPH, EDGE> lpt(G);
      for (i = 0; i < N; i++)
        cout << i << " " << lpt.dist(i) << endl;
    }

Предположим, что в пример, представленный на рис. 21.24, нужно добавить ограничение, состоящее в том, что работа 2 должна начаться не позже заданного количества единиц времени с после начала работы 4. Если с больше 0.53, то полученное расписание укладывается в заданные рамки, поскольку оно предписывает начать работу 2 в момент 1.23, что соответствует задержке на 0.53 после окончания работы 4 (которая начинается в момент 0.70). Если с меньше 0.53, то можно удовлетворить это ограничение, сдвинув начало работы 4 на более позднее время. Если работа 4 длится долго, то это изменение может увеличить время завершения всего графика. Хуже, если существуют другие ограничения на работу 4 , и мы не можем переместить время ее начала. Вообще-то бывают ограничения, которым не может удовлетворить ни одно расписание. Например, в нашем примере не удастся удовлетворить таким ограничениям, при которых работа 2 должна начаться раньше чем через d единиц времени после начала работы 6, для d меньшего 0.53, т.к. из ограничений, что работа 2 должна следовать за 8, а 8 за 6, следует, что работа 2 должна начаться позже, чем через 0.53 единицы времени после начала работы 6.

Если добавить в наш пример оба ограничения, рассмотренные в предыдущем абзаце, то, в зависимости от значений с и d, каждое ограничение повлияет на момент начала работы 4 в расписании, на время завершения всего графика, а также на то, существует ли выполнимый календарный график. Добавление дополнительных подобных ограничений увеличивает количество возможностей и превращает легкую задачу в трудную. Так что мы имеем все основания искать способ сведения этой задачи к некоторой известной задаче.

Лемма 21.16. Задача календарного планирования с конечными сроками сводится к задаче поиска кратчайших путей (с возможностью существования отрицательных весов).

Доказательство. Преобразуем ограничения предшествования в неравенства, используя то же сведение, что и описанное в свойстве 21.14. Для каждого ограничения конечного срока добавим неравенство 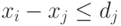$x_{i}-x_{j} \leq d_{j}$ , что эквивалентно $x_{j}-x_{i} \leq -d_{j}$ , где d_j - положительная константа. Преобразуем множество неравенств в сеть, применив то же сведение, что и описанное в лемме 21.15. Изменим знаки всех весов. Такое же построение, что и в доказательстве леммы 21.15, позволяет показать, что любое дерево кратчайших путей в сети с корнем в 0 будет соответствовать графику. $\blacksquare$

Это сведение подводит нас к вопросу о кратчайших путях с отрицательными весами. Оно утверждает, что если можно найти эффективное решение задачи поиска кратчайших путей с отрицательными весами, то можно найти эффективное решение задачи планирования работ с конечными сроками. (Опять-таки, соответствие в доказательстве леммы 21.16 не означает наличие обратного утверждения (см. упражнение 21.91).)

Добавление конечных сроков в задачу планирования работ соответствует допущению отрицательных констант в задаче разностных ограничений и отрицательных весов в задаче о кратчайших путях. (Это изменение требует также изменения задачи разностных ограничений, чтобы правильно обрабатывать аналог отрицательных циклов в задаче о кратчайших путях.) Эти более общие варианты задач сложнее для решения, чем рассмотренные вначале варианты, но, скорее всего, они и более полезны как обобщенные модели. Похоже, что приемлемый способ решения всех их следует искать в эффективном решении задачи поиска кратчайших путей с отрицательными весами.

К сожалению, с этим подходом связана принципиальная трудность, которая демонстрирует другую сторону вопроса применения сведения, позволяющую оценить относительную трудность задач. Мы уже использовали сведение в положительном смысле - для расширения применимости решений к общим задачам, однако его можно использовать и в отрицательном смысле - чтобы показать пределы такого расширения.

Трудность заключается в крайней сложности решения общей задачи поиска кратчайших путей. Далее мы увидим, как концепция сведения помогает сформулировать данное утверждение точно и обоснованно. В "Виды графов и их свойства" было рассмотрено множество задач, известных как NP-трудные, которые считаются трудноразрешимыми, т.к. все известные алгоритмы их решения в худшем случае требуют экспоненциального времени. Сейчас мы покажем, что в общем случае задача поиска кратчайших путей является NP-трудной.

Как кратко упомянуто в "Виды графов и их свойства" и будет подробно рассмотрено в части VIII, обычно мы считаем, что если задача является NP-трудной, то это означает не только то, что не известно эффективного алгоритма, гарантирующего решение этой задачи, но и то, что все-таки имеется некоторая надежда найти такой алгоритм. В этом контексте мы используем термин эффективный по отношению к алгоритмам, время выполнения в худшем случае которых ограничено некоторой полиномиальной функцией от размера входных данных. Открытие эффективного алгоритма решения любой NP-трудной задачи должно быть ошеломляющим научным достижением. Концепция NP-трудности является важной для идентификации трудноразрешимых задач, т.к. часто легко доказать, что задача NP-трудна, используя следующую методику.

Лемма 21.17. Задача является NP-трудной, если существует эффективное сведение к ней любой NP-трудной задачи.

Эта лемма зависит от строгого определения эффективного сведения одной задачи A к другой задаче B. Мы отложим такие определения до части VIII (обычно применяются два различных определения). А пока мы просто используем этот термин для описания случая, когда существуют эффективные алгоритмы как для преобразования задачи A в задачу B, так и для преобразования решения B в решение A.

Теперь предположим, что имеется эффективное сведение NP-трудной задачи A к конкретной задаче B. Проведем доказательство от противного: если существует эффективный алгоритм для B, то мы могли бы воспользоваться им для решения с помощью сведения любого экземпляра задачи A за полиномиальное время (преобразуем данный экземпляр A в экземпляр B, решаем эту задачу, а затем преобразуем полученное решение). Однако не существует известного алгоритма, который гарантировал бы такое решение для A (поскольку A является NP-трудной), поэтому предположение о существовании алгоритма с полиномиальным временем для задачи B неверно, т.е. B также является NP-трудной задачей. $\blacksquare$

Эта методика является чрезвычайно важной, поскольку она позволяет показать, что огромное множество задач относятся к NP-трудным, предоставляя на выбор широкий круг задач, с помощью которых строились доказательства NP-трудности новой задачи. Например, в "Виды графов и их свойства" мы столкнулись с одной из классических NP-трудных задач - с задачей поиска гамильтонова пути, где нужно определить, существует ли простой путь, содержащий все вершины данного графа. Она была одной из первых задач, в отношении которой было показано, что она является NP-трудной (см. раздел ссылок). Ее нетрудно сформулировать в виде задачи поиска кратчайших путей, и поэтому из леммы 21.17 следует, что задача кратчайших путей относится к NP-трудным:

Лемма 21.18. В сетях, в которых веса ребер могут быть отрицательными, задачи поиска кратчайших путей являются NP-трудными.

Доказательство. Наше доказательство основано на сведении задачи о гамильтоновом пути к задаче о кратчайших путях. То есть мы покажем, что для решения задачи о гамильтоновом пути можно использовать любой алгоритм, позволяющий найти кратчайшие пути в сетях с отрицательными весами ребер. Для заданного неориентированного графа построим сеть с ребрами в обоих направлениях, соответствующими каждому ребру в графе, и присвоим каждому ребру вес -1. Кратчайший (простой) путь, начинающийся в любой вершине этой сети, имеет длину 1 - V тогда и только тогда, когда в графе существует гамильтонов путь. Обратите внимание, что эта сеть изобилует отрицательными циклами. Не только каждый цикл в графе соответствует отрицательному циклу в сети, но и каждое ребро в графе соответствует циклу с весом -2 в данной сети.

Из этого построения следует, что задача поиска кратчайших путей является NP-трудной, поскольку если бы мы могли разработать эффективный алгоритм для задачи поиска кратчайших путей в сетях, то мы имели бы эффективный алгоритм для задачи поиска гамильтонова пути в графах. $\blacksquare$

Если мы обнаруживаем, что данная задача является NP-трудной, естественно начать искать те варианты этой задачи, которые можно решить. Для задач поиска кратчайших путей мы имеем массу эффективных алгоритмов для ациклических сетей или для сетей, в которых веса ребер не являются отрицательными, и отсутствие хорошего решения для сетей, которые могут содержать циклы и отрицательные веса. Существуют ли какие-либо другие виды сетей, которые нас могут заинтересовать? Эта тема будет рассмотрена в разделе 21.7. Там, например, будет показано, что задача календарного планирования с конечными сроками сводится к варианту задачи поиска кратчайших путей, которую можно эффективно решить. Это обычная ситуация: при переходе ко все более трудным вычислительным задачам мы пытаемся выявить такие варианты данных задач, для которых мы надеемся найти решение.

Как показывают эти примеры, сведение является простой технологией, которая полезна при разработке алгоритмов, и поэтому мы часто прибегаем к нему. При этом мы либо сможем решить новую задачу, доказав, что она сводится к задаче с известным решением, либо сможем доказать, что новая задача будет сложной, показав, что задача, о которой известно, что она сложная, сводится к рассматриваемой задаче.

В таблице 21.3 приведен более подробный перечень различных выводов из сведения между четырьмя общими классами задач, которые были рассмотрены в "Виды графов и их свойства" . Обратите внимание на несколько случаев, когда сведение не дает новой информации: например, хотя выборка и сводится к сортировке, а задача поиска наиболее длинных путей в ациклических сетях сводится к задаче поиска кратчайших путей в сетях общего вида, эти факты не проливают свет на относительную трудность задачи. В других случаях сведение либо может, либо нет, предоставить новую информацию; еще в некоторых случаях выводы действительно глубоки. Для развития этих концепций требуется строгое и формальное описание концепции сведения, но об этом мы подробно поговорим в части 8, а здесь просто подведем неформальный итог наиболее важных практических применений сведения вместе с уже знакомыми нам примерами.

В этой таблице приведены некоторые выводы из сведения задачи A к другой задаче B, с примерами, которые были рассмотрены в этом разделе. Глубокие выводы из случаев 9 и 10 ведут настолько далеко, что мы в общем случае предполагаем, что обосновать такие сведения невозможно (см. часть VIII). Сведение наиболее полезно в случаях 1, 6, 11 и 16 - для изучения нового алгоритма для A или обоснования нижней границы для B; 13-15 - для изучения новых алгоритмов для A; 12 - чтобы оценить сложность B.

Таблица 21.3. Выводы из сведения
A	B	Вывод из сведения $A\Rightarrow B$	Пример
1 Простая	Простая	Новая нижняя граница B	Сортировка $\Rightarrow EMST$
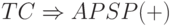
2 Простая	Разрешимая	Нет	$TC\Rightarrow APSP(+)$
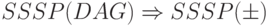
3 Простая	Трудноразрешимая	Нет	$SSSP(DAG)\Rightarrow SSSP(\pm)$
4 Простая	Решение не известно	Нет
5 Разрешимая	Простая	A простая
6 Разрешимая	Разрешимая	Новое решение A	$DC(+)\Rightarrow SSSP(DAG)$
7 Разрешимая	Трудноразрешимая	Нет
8 Разрешимая	Решение не известно	Нет
9 Трудноразрешимая	Простая	Глубокий
10 Трудноразрешимая	Разрешимая	Глубокий
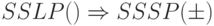
11 Трудноразрешимая	Трудноразрешимая	Так же, как 1 или 6	$SSLP(\p)\Rightarrow SSSP(\pm)$
12 Трудноразрешимая	Решение не известно	B неразрешимая	$HP\Rightarrow SSSP(\pm)$
13 Решение не известно	Простая	A простая	$JS\Rightarrow SSSP(DAG)$
14 Решение не известно	Разрешимая	A разрешимая
15 Решение не известно	Трудноразрешимая	A разрешимая
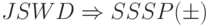
16 Решение не известно	Решение не известно	Так же, как 1 или 6	$JSWD\Rightarrow SSSP(\pm)$

Обозначения:
EMST	минимальное евклидово остовное дерево
TC	транзитивное замыкание
APSP	кратчайшие пути для всех пар вершин
SSSP	кратчайшие пути из одного истока
SSLP	наиболее длинные пути из одного истока
(+)	(в сетях с неотрицательными весами)
(±)	(в сетях с весами, которые могут быть отрицательными)	(DAG)	(в ациклических сетях)
DC	разностные ограничения
HP	гамильтоновы пути
JS(WD)	планирование заданий (с конечными сроками)

Верхние границы. Если существует эффективный алгоритм решения задачи B, и можно доказать, что A сводится к B, то существует эффективный алгоритм и для решения задачи A. Возможно, существует другой, лучший, алгоритм для A, однако эффективность B является верхней границей того, чего можно достичь для A. Например, доказательство того, что задача календарного планирования сводится к задаче поиска наиболее длинных путей в ациклических сетях, превращает наш алгоритм решения второй задачи в эффективный алгоритм решения первой задачи.

Нижние границы. Если известно, что любой алгоритм для задачи A требует определенных ресурсов, и можно доказать, что A сводится к B, то мы знаем, что B имеет, по крайней мере, такие же требования к ресурсам, т.к. из существования лучшего алгоритма для B следовало бы существование лучшего алгоритма для A (если стоимость сведения меньше стоимости алгоритма B). То есть эффективность A равна нижней границе того, что можно получить в лучшем случае для B. Например, эта технология применялась в "Орграфы и DAG-графы" , чтобы показать, что вычисление транзитивного замыкания имеет такую же трудоемкость, как умножение логических матриц, и в "Минимальные остовные деревья" - чтобы показать, что вычисление евклидова MST так же трудоемко, как сортировка.

Трудноразрешимость. В частности, можно доказать, что некоторая задача трудноразрешима, показав, что к ней сводится другая трудноразрешимая задача. Например, из леммы 21.18 следует, что задача поиска кратчайших путей трудноразрешима, поскольку к ней сводится задача поиска гамильтонова пути, которая является трудноразрешимой.

Кроме этих общих выводов, ясно, что более детальная информация об эффективности конкретных алгоритмов для решения конкретных задач может непосредственно относиться к другим задачам, которые сводятся к первым. Когда мы находим верхнюю границу, мы можем анализировать соответствующий алгоритм, проводить эмпирические исследования и т.п., чтобы определить, получено ли лучшее решение задачи. Во время разработки качественного универсального алгоритма можно затратить усилия на разработку и тестирование качественной реализации и затем создать соответствующие АТД, которые расширяют ее сферу применения.

Мы используем сведение в качестве базового инструментального средства в этой и следующей лекциях. Мы будем делать упор на общей применимости рассматриваемых задач и общей применимости решающих их алгоритмов - за счет сведения к ним других задач. Важно также иметь представление об иерархической структуре все более общих формулировок задач. Например, линейное программирование является общей формулировкой, которая важна не только потому, что к ней сводятся многие задачи, но и потому, что известно, что эта задача не относится к NP-трудным. Другими словами, нет известного способа сведения общей задачи поиска кратчайших путей (или любой другой NP-трудной задачи) к линейному программированию. Подобные вопросы будут рассмотрены в части VIII.

Не все задачи являются разрешимыми, но уже разработаны хорошие общие модели, подходящие для широкого класса задач, для которых известны методы решения. Наш первый пример такой модели - кратчайшие пути в сетях. Продвигаясь ко все более общим задачам, мы попадем в область исследования операций, которая изучает математические методы принятия решений, и главной целью которой является разработка и изучение таких моделей. Одна важная проблема в исследовании операций - поиск модели, которая наиболее удобна для решения задачи, а затем подгонка задачи под эту модель. Эта область исследований известна также как математическое программирование (название дано еще до компьютерной эпохи и новой трактовки слова " программирование " ).

Сведение - это современная концепция, которая по сути аналогична математическому программированию и является основой нашего понимания трудоемкости вычислений для широкого круга приложений.

Упражнения

21.85. При помощи сведения, описанного в лемме 21.12, разработайте реализацию транзитивного замыкания (с тем же интерфейсом, что и в программах 19.3 и 19.4), которая использует АТД поиска кратчайших путей для всех пар вершин из раздела 21.3.

21.86. Покажите, что задача вычисления количества сильных компонентов в орграфе сводится к задаче поиска кратчайших путей для всех пар вершин с неотрицательными весами.

21.87. Приведите задачи разностных ограничений и кратчайших путей, которые соответствуют (аналогично построению лемм 21.14 и 21.15) задаче календарного планирования, где работы 0-7 имеют, соответственно, длины

0.40.20.30.40.20.50.1

и ограничения

5-14-66-03-26-16-2.

21.88. Приведите решение задачи календарного планирования из упражнения 21.87.

21.89. Предположим, что работы из упражнения 21.87 имеют дополнительные ограничения: работа 1 должна начаться до окончания работы 6, а работа 2 должна начаться до окончания работы 4 . Приведите задачу поиска кратчайших путей, к которой сводится эта задача, воспользовавшись построением из доказательства леммы 21.16.

21.90. Покажите, что задача поиска наиболее длинных путей для всех пар вершин в ациклических сетях с положительными весами сводится к задаче разностных ограничений с положительными константами.

21.91. Объясните, почему соответствие в доказательстве леммы 21.16 нельзя расширить для доказательства того, что задача поиска кратчайших путей сводится к задаче календарного планирования с конечными сроками.

21.92. Усовершенствуйте программу 21.8, чтобы работам можно было присваивать не только целочисленные номера, но и символические имена (см. программу 17.10).

21.93. Разработайте интерфейс АТД, который дает возможность клиентам ставить и решать задачи разностных ограничений.

21.94. Напишите класс, который реализует интерфейс из упражнения 21.93 на основе сведения задачи разностных ограничений к задаче поиска кратчайших путей в ациклических сетях.

21.95. Разработайте реализацию класса, который решает задачу поиска кратчайших путей из одного истока в ациклических сетях с отрицательными весами с помощью сведения к задаче разностных ограничений и интерфейса из упражнения 21.93.

21.96. Решение задачи поиска кратчайших путей в ациклических сетях из упражнения 21.95 предполагает существование реализации, которая решает задачу разностных ограничений. Что произойдет, если использовать реализацию из упражнения 21.94, которая предполагает существование реализации для задачи поиска кратчайших путей в ациклических сетях?

21.97. Докажите эквивалентность любых двух NP-трудных задач (т.е. выберите две таких задачи и докажите, что они сводятся друг к другу).

21.98. Сформулируйте явное построение, которое сводит задачу поиска кратчайших путей в сетях с целочисленными весами к задаче поиска гамильтонова пути.

21.99. Пользуясь сведением, разработайте класс, который использует АТД сети и решает задачу поиска кратчайших путей из одного истока, чтобы решить следующую задачу. Для заданного орграфа, вектора положительных весов, индексированного именами вершин, и начальной вершины v нужно найти такие пути из v в каждую другую вершину, чтобы сумма весов вершин в пути была минимальной.

21.100. Программа 21.8 не проверяет, разрешима ли задача календарного планирования, которую она выбирает в качестве входной (существует ли цикл). Охарактеризуйте графики, которые программа будет выводить для неразрешимых задач.

21.101. Разработайте интерфейс АТД, который позволяет клиентам ставить и решать задачи календарного планирования. Напишите класс, который реализует полученный интерфейс на основе сведения задачи календарного планирования работ к задаче поиска кратчайших путей в ациклических сетях (как в программе 21.8).

21.102. Добавьте в класс из упражнения 21.101 функцию (вместе с реализацией), которая выводит наиболее длинный путь в графике. (Такой путь обычно называется критическим путем.)

21.103. Напишите клиент для интерфейса из упражнения 21.101, который генерирует PostScript-программу для прорисовки календарного графика в стиле рис. 21.24 (см. "Абстрактные типы данных" 3).

21.104. Разработайте модель для генерации задач календарного планирования. Воспользуйтесь полученной моделью для тестирования реализаций из упражнений 21.101 и 21.103 на приемлемом множестве задач разных размеров.

21.105. Напишите класс, который реализует интерфейс из упражнения 21.101, решая задачу календарного планирования работ с помощью ее сведения к задаче разностных ограничений.

21.106. Диаграмма PERT (Project Evaluation and Review Technique - сетевое планирование и управление) - это сеть, которая представляет задачу календарного планирования с ребрами в качестве работ (см. рис. 21.25). Напишите класс, реализующий интерфейс календарного планирования из упражнения 21.101 на основе диаграмм PERT.

21.107. Сколько вершин содержит диаграмма PERT для задачи планирования с V работами и E ограничениями?

21.108. Напишите программы для взаимного преобразования задач календарного планирования работ, представленных ребрами (диаграммы PERT, см. упражнение 21.106), и представленных вершинами (см. рис. 21.22).

Рис. 21.25. Диаграмма PERT

Диаграмма PERT - это сетевое представление задачи календарного планирования, где работы представлены ребрами. Сеть в верхней части рисунка является представлением задачи календарного планирования с рис. 21.22, где работы 0-9 представлены, соответственно, ребрами 0-1, 1-2, 2-3, 4-3, 5-3, 0-3, 5-4, 1-4, 4-2 и 1-5. Критическим путем в этом графике является наиболее длинный путь в данной сети.

Дальше >>

Авторизоваться

Алгоритмы на С++

Кратчайшие пути

Вопросы и ответы