|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Кратчайшие пути
Евклидовы сети
В приложениях, где сети моделируют топографические карты, часто бывает нужно найти наилучший маршрут из одного места в другое. В данном разделе мы рассмотрим стратегию решения этой задачи - быстрый алгоритм для задачи поиска кратчайшего пути с несколькими истоками и стоками в евклидовых сетях (Euclidean network), вершины которых являются точками на плоскости, а веса ребер определяются геометрическими расстояниями между их вершинами.
Эти сети обладают двумя важными свойствами, которые не обязательно присущи весам ребер в общем случае. Во-первых, расстояния удовлетворяют неравенству треугольника: расстояние от s до d никогда не больше, чем расстояние от s до x плюс расстояние от x до d. Во-вторых, координаты вершин дают нижнюю границу длины пути: не существует пути из s в d, который был бы короче расстояния между s и d по прямой. Алгоритм поиска кратчайших путей для задачи с одним истоком и стоком, который мы рассмотрим в этом разделе, использует эти два свойства для повышения его эффективности.
Зачастую евклидовы сети симметричны, т.е. их ребра являются двунаправленными. Как было сказано в начале этой главы, такие сети возникают, например, если интерпретировать представление взвешенного неориентированного евклидового графа матрицей смежности или списками смежности (см. "Минимальные остовные деревья" ) как взвешенный орграф (сеть). Когда мы рисуем неориентированную евклидову сеть, мы имеем в виду как раз такую интерпретацию, чтобы не плодить стрелки на рисунках.
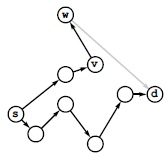
Основная идея проста: поиск по приоритетам предоставляет общий механизм для поиска путей в графах. С помощью алгоритма Дейкстры мы рассматриваем пути в порядке увеличения их расстояния от начальной вершины. Это упорядочение гарантирует, что по достижении стока будут просмотрены все более короткие пути в графе, ни один из которых не привел в сток. Но в евклидовом графе имеется дополнительная информация: если мы ищем путь из истока s в сток d и встречаем третью вершину v, то мы знаем, что нам не только необходимо учесть путь, найденный из s в v, но и что лучшее, что можно сделать при проходе из v в d - это сначала пройти по ребру v-w, а затем найти путь, длина которого равна расстоянию от w до d по прямой (см. рис. 21.18). Поиск по приоритетам позволяет легко учесть эту дополнительную информацию для повышения эффективности вычислений. Мы используем стандартный алгоритм, но в качестве приоритета для каждого ребра v-w принимаем сумму следующих трех величин: длина известного пути из s в v, вес ребра v-w, и расстояние от w до t. Если всегда выбирать ребро с наименьшей такой величиной, то по достижении вершины t мы будем уверены, что в данном графе не существует более короткого пути из s в t. Кроме того, в типичных сетях мы приходим к этому заключению после выполнения гораздо меньшего объема работы, чем при использовании алгоритма Дейкстры.
Вычисляя кратчайшие пути в евклидовом графе, в операции релаксации можно учитывать расстояния до конечной вершины. В данном примере можно сделать вывод, что показанный путь из s в v с добавленным ребром v-w не может привести к более короткому пути из s в d, чем уже найденный, т.к. длина любого такого пути должна быть не меньше длины пути из s в v плюс длина v-w и плюс расстояние от w до d по прямой, что больше длины известного пути из s в d. Подобные проверки могут существенно уменьшить количество рассматриваемых путей.
Для реализации данного подхода мы используем стандартную алгоритма Дейкстры на основе PFS (см. программу 21.1, поскольку евклидовы графы обычно разрежены, а также упражнение 21.73) с двумя изменениями. Во-первых, вместо обнуления элементов wt[s] в начале поиска они заполняются величинами distance(s, d), где distance() - функция, возвращающая расстояние между двумя вершинами. Во-вторых, мы определяем приоритет P как функцию
(wt[v] + e->wt() + distance(w, d) - distance(v, d))
вместо функции (wt[v] + e->wt0), которая использовалась в программе 21.1 (вспомните, что v и S - это локальные переменные, в которые заносятся, соответственно, величины e->v() и e->w()). Эти изменения, которые мы будем называть евклидовой эвристикой (Euclidean heuristic), сохраняют неизменным свойство, что величина wt[v] - distance(v, d) является длиной кратчайшего пути в сети из s в v для каждой вершины v (следовательно, wt[v] содержит нижнюю границу длины самого короткого из всех возможных путей из s в d через v). Величина wt[w] вычисляется добавлением к этой величине веса ребра (расстояние до w) плюс расстояние от w до стока d.
Лемма 21.11. Поиск по приоритетам с евклидовой эвристикой решает задачу кратчайших путей из истока в сток в евклидовых графах.
Доказательство. Здесь применимо доказательство леммы 21.2. В момент включения вершины x в дерево добавление расстояния между x и d к приоритету не влияет на то, что путь в дереве из s в x является кратчайшим путем в графе из s в x, поскольку к длине всех путей, ведущих в x, добавляется одна и та же величина.
Когда вершина d включена в дерево, мы знаем, что никакой другой путь из s в d не короче, чем путь по дереву, т.к. любой такой путь должен состоять из некоторого пути в дереве, за которым следует ребро, ведущее в некоторую вершину w вне дерева, а в конце находится путь из w в d (длина которого не может быть короче расстояния между w и d). Однако по построению мы знаем, что длина пути из s в w плюс расстояние от w до d не меньше длины пути по дереву из s в d. 
В разделе 21.6 мы обсудим другой простой способ реализации евклидовой эвристики. Сначала мы перебираем все ребра графа, изменяя веса ребер: для каждого ребра v-w мы добавляем к весу величину distance(w, d) -distance(v, d). Затем выполняем стандартный алгоритм поиска кратчайшего пути, начиная с s (элемент wt[s] содержит значение distance(s,d)), и останавливаемся по достижении d. Этот метод в вычислительном отношении эквивалентен уже описанному методу (который вообще-то при своей работе вычисляет те же веса) и является конкретным примером базовой операции, которая называется перевзве-шивание (reweighting) сети. Перевзвешивание играет важную роль при решении задач поиска кратчайших путей с отрицательными весами; мы обсудим его подробно в разделе 21.6.
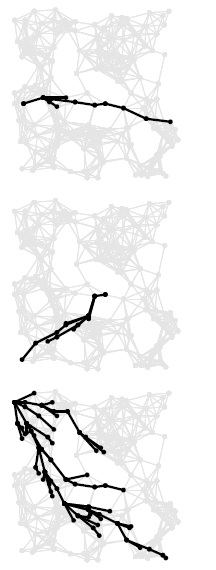
Во время поиска кратчайшего пути в конечную вершину можно ограничить поиск вершинами внутри относительно небольшого эллипса вокруг пути, как показано в этих трех примерах, на которых изображены SPT-поддеревья для примеров с рис. 21.12.
Евклидова эвристика влияет на эффективность, но не на правильность алгоритма Дейкстры для вычисления кратчайших путей из истока в сток. Как было сказано в доказательстве леммы 21.2, применение стандартного алгоритма для решения задачи с одним истоком и стоком означает построение SPT, в котором все вершины ближе к началу, чем сток d. При использовании евклидовой эвристики SPT содержит только те вершины, для которых длина пути из s плюс расстояние до d меньше длины кратчайшего пути из s в d. Мы надеемся, что для многих приложений это дерево будет значительно меньшим, поскольку эвристика отбрасывает существенное количество длинных путей. Точный выигрыш зависит от структуры графа и геометрии расположения вершин. На рис. 21.19 показано действие евклидовой эвристики на нашем демонстрационном графе, где выигрыш существенен. Мы называем этот метод эвристикой, поскольку выигрыш не гарантирован: всегда возможен случай, когда имеется единственный длинный путь, который может уйти произвольно далеко в сторону от истока и лишь затем направиться к стоку (см. упражнение 21.80).
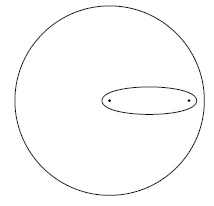
На рис. 21.20 наглядно демонстрируется геометрический смысл евклидовой эвристики: если длина кратчайшего пути из s в d равна z, то вершины, просматриваемые этим алгоритмом, лежат приблизительно внутри эллипса, определяемого как геометрическое место точек х, для которых расстояние от s до x плюс расстояние от х до d равно z. Для типичных евклидовых графов ожидаемое количество вершин в этом эллипсе намного меньше, чем количество вершин в круге радиуса z с центром в истоке (которые просматриваются алгоритмом Дейкстры).
При продвижении к конечной вершине во время поиска кратчайшего пути можно ограничиться вершинами внутри эллипса, описанного вокруг пути, вместо круга с центром в истоке s, как в алгоритме Дейкстры. Радиус круга и форма эллипса определяются длиной кратчайшего пути.
Точный анализ получаемой экономии - трудная аналитическая задача, которая зависит от вида как множества случайных точек, так и случайных графов (см. раздел ссылок). В типичных ситуациях мы ожидаем, что если стандартный алгоритм при вычислении кратчайшего пути из истока в сток рассматривает X вершин, то евклидова эвристика сократит трудоемкость до величины, пропорциональной 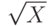 , и тогда ожидаемое время выполнения будет пропорционально V для насыщенных графов и
, и тогда ожидаемое время выполнения будет пропорционально V для насыщенных графов и  для разреженных. Этот пример показывает, что трудность разработки подходящей модели или анализа связанных с ней алгоритмов не должна удерживать нас от использования значительного выигрыша, который возможен во многих приложениях, особенно если реализация тривиальна.
для разреженных. Этот пример показывает, что трудность разработки подходящей модели или анализа связанных с ней алгоритмов не должна удерживать нас от использования значительного выигрыша, который возможен во многих приложениях, особенно если реализация тривиальна.
Доказательство леммы 21.11 применимо к любой функции, которая дает нижнюю границу расстояния от каждой вершины до d. Существуют ли другие функции, для которых алгоритм будет рассматривать еще меньше вершин, чем евклидова эвристики? Данный вопрос изучался в общей постановке применительно к широкому классу алгоритмов комбинаторного поиска. Вообще-то евклидова эвристика является одним из вариантов алгоритма, называемого A* (произносится " эй-стар " ). Эта теория утверждает, что оптимальной будет функция, которая дает наилучшую возможную нижнюю границу; другими словами, чем лучше эта граничная функция, тем более эффективен поиск. В данном случае оптимальность A* говорит о том, что евклидова эвристика наверняка просмотрит не больше вершин, чем алгоритм Дейкстры (который представляет собой A* с нулевой нижней границей). Результаты аналитических исследований дают более точную информацию для конкретных моделей случайных сетей.
Свойства евклидовых сетей можно использовать и для облегчения создания абстрактных АТД поиска кратчайших путей, более эффективно реализующих компромисс между используемым временем и памятью, чем для сетей общего вида (см. упражнения 21.48-21.50). Такие алгоритмы важны в приложениях наподобие обработки географических карт, где возникают огромные разреженные сети. Например, предположим, что требуется разработать навигационную систему, определяющую кратчайшие пути на карте с миллионами дорог. Возможно, саму карту можно хранить непосредственно в небольшом бортовом компьютере, однако матрицы расстояний и путей зачастую слишком велики для этого (см. упражнения 21.39 и 21.40); поэтому алгоритмы поиска всех путей из раздела 21.3 не применимы. Алгоритм Дейкстры также может не обеспечить достаточно быстрых ответов для огромных карт. В упражнениях 21.77 и 21.78 рассматриваются стратегии рационального соотношения между объемом предварительной обработки и объемом памяти, которые обеспечивают быструю реакцию на запросы о кратчайших путях из истока в сток.
Упражнения
21.68. Найдите в инернете большой евклидов граф - возможно, карту с таблицей расстояний между пунктами, телефонную сеть со стоимостями переговоров или расписание авиарейсов с указанными стоимостями билетов.
21.69. Используя стратегии, описываемые в упражнениях 17.71-17.73, напишите программы, которые генерируют случайные евклидовы графы, соединяя вершины, расположенные на решетке 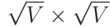 .
.
21.70. Покажите, что частичное SPT, вычисленное евклидовой эвристикой, не зависит от значения, которое вначале заносится в wt[s]. Объясните, как вычислять длины кратчайших путей из начального значения.
2l.71. Покажите в стиле рис. 21.10 результат применения евклидовой эвристики для вычисления кратчайшего пути из 0 в 6 в сети из упражнения 21.1.
21.72. Опишите, что произойдет, если функция distance(s, t), используемая в евклидовой эвристике, возвращает фактическую длину кратчайшего пути из s в t для всех пар вершин.
21.73. Разработайте реализацию класса для поиска кратчайших путей в насыщенных евклидовых графах, основанную на представлении графа, которое поддерживает функцию edge и реализацию алгоритма Дейкстры (программа 20.6 с соответствующей функцией вычисления приоритета).
21.74. Эмпирически проверьте эффективность евклидовой эвристики поиска кратчайших путей для различных евклидовых сетей (см. упражнения 21.9, 21.68, 21.69 и 21.80). Для каждого графа сгенерируйте V/10 случайных пар вершин и выведите таблицу со следующими величинами: среднее расстояние между вершинами; средняя длина кратчайшего пути между вершинами; среднее отношение количества вершин, просматриваемых евклидовой эвристикой, к количеству вершин, просматриваемых алгоритмом Дейкстры; и среднее отношение площади эллипса, соответствующего евклидовой эвристике, к площади круга, соответствующего алгоритму Дейкстры.
21.75. Разработайте реализацию класса для задачи поиска кратчайших путей из истока в сток на евклидовых графах, которая основывается на двунаправленном поиске, описанном в упражнении 21.35.
21.76. Воспользуйтесь геометрической интерпретацией для оценки отношения количества вершин в SPT, создаваемом алгоритмом Дейкстры для задачи с истоком и стоком, к количеству вершин в SPT, создаваемом двунаправленной реализацией из упражнения 21.75.
21.77. Разработайте реализацию класса для поиска кратчайших путей в евклидовых графах, которая выполняет в конструкторе следующий шаг предварительной обработки: накладывает на район карты сетку  , а затем при помощи алгоритма Флойда поиска кратчайших путей для всех пар вершин вычисляет матрицу
, а затем при помощи алгоритма Флойда поиска кратчайших путей для всех пар вершин вычисляет матрицу  , элемент которой на пересечении строки i и столбца j содержит длину кратчайшего пути, соединяющего любую вершину из квадрата сетки i с любой вершиной из квадрата j. Затем используйте эти длины кратчайших путей в качестве нижних границ для усовершенствования евклидовой эвристики. Проведите эксперименты для нескольких различных значений W, которые дают небольшое ожидаемое количество вершин в квадрате решетки.
, элемент которой на пересечении строки i и столбца j содержит длину кратчайшего пути, соединяющего любую вершину из квадрата сетки i с любой вершиной из квадрата j. Затем используйте эти длины кратчайших путей в качестве нижних границ для усовершенствования евклидовой эвристики. Проведите эксперименты для нескольких различных значений W, которые дают небольшое ожидаемое количество вершин в квадрате решетки.
21.78. Разработайте реализацию АТД поиска кратчайших путей для всех пар вершин в евклидовых графах, которая объединяет идеи, изложенные в упражнениях 21.75 и 21.77.
21.79. Эмпирически сравните эффективность эвристик, описанных в упражнениях 21.75-21.78, для различных евклидовых сетей (см. упражнения 21.9, 21.68, 21.69 и 21.80).
21.80. Расширьте эмпирические исследования, включив в них евклидовы графы, которые получаются удалением всех вершин и ребер из круга радиуса r в центре, для r = 0.1, 0.2, 0.3 и 0.4. (Эти графы обеспечивают серьезную проверку евклидовой эвристики.)
21.81. Приведите прямую реализацию алгоритма Флойда, которая позволит реализовать АТД сети для неявных евклидовых графов, определяемых N точками на плоскости с ребрами, которые соединяют друг с другом точки на расстоянии не больше d. Не представляйте эти графы явным образом; вместо этого для заданных двух вершин вычислите расстояние между ними, чтобы определить, существует ли ребро, и если да, то чему равна его длина.
21.82. Разработайте реализацию, описанную в упражнении 21.81, которая строит граф с соседними связями, а затем применяет к каждой вершине алгоритм Дейкстры (см. программу 21.1).
21.83. Эмпирически сравните время выполнения и объем памяти, необходимые для алгоритмов из упражнений 21.81 и 21.82, для d = 0.1, 0.2, 0.3 и 0.4.
21.84. Напишите клиентскую программу, которая выполняет динамическую графическую анимацию работы евклидовой эвристики. Программа должна создать изображения наподобие рис. 21.19 (см. упражнение 21.38). Протестируйте программу на различных евклидовых сетях (см. упражнения 21.9, 21.68, 21.69 и 21.80).