|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Кратчайшие пути
Алгоритм Дейкстры
В "Минимальные остовные деревья" был рассмотрен алгоритм Прима для нахождения минимального остовного дерева (MST) взвешенного неориентированного графа: мы строим его, добавляя на каждом шаге кратчайшее ребро, которое соединяет вершину из MST с вершиной, еще не входящей в MST. Для вычисления SPT можно воспользоваться почти такой же схемой. Вначале мы заносим в SPT исток, а затем строим SPT, добавляя на каждом шаге одно ребро, которое формирует кратчайший путь из истока в вершину, не включенную в SPT. То есть вершины заносятся в SPT в порядке их расстояния (по SPT-дереву) от начальной вершины. Этот метод называется алгоритмом Дейкстры (Dijkstra).
Как обычно, необходимо различать неформальное описание алгоритма на некотором уровне абстракции и различные конкретные реализации (как в программе 21.1). Эти реализации различаются в основном представлением графа и реализациями очереди с приоритетами, даже если такие различия не всегда приводятся в литературе. Когда мы убедимся, что алгоритм Дейкстры корректно вычисляет кратчайшие пути из одного истока, мы рассмотрим другие реализации алгоритма и обсудим их связь с программой 21.1.
Лемма 21.2. Алгоритм Дейкстры решает задачу поиска кратчайших путей из одного истока в сетях с неотрицательными весами.
Доказательство. Для заданной вершины-истока s необходимо убедиться, что пути из корня s в каждую вершину х в дереве, вычисленному алгоритмом Дейкстры, соответствуют кратчайшим путям в графе из s в х. Это можно доказать по индукции. Допустим, что вычисленное на данный момент поддерево обладает этим свойством - нам нужно лишь доказать, что добавление новой вершины х приводит к добавлению кратчайшего пути в эту вершину. Однако все другие пути, ведущие в х, должны начинаться путем в дереве и завершаться ребром в вершину, которая не находится в дереве. По построению все такие пути являются более длинными, чем рассматриваемый путь из s в х.
Таким же образом можно показать, что алгоритм Дейкстры решает задачу поиска кратчайших путей из истока в сток, если начать с истока и остановиться, когда сток покинет очередь с приоритетами. 
Доказательство не срабатывает, если веса ребер могут быть отрицательными, поскольку в нем предполагается, что при добавлении ребер к пути длина пути не уменьшается. В сети с отрицательными весами ребер это предположение недействительно, поскольку любое встреченное ребро, ведущее в некоторую вершину дерева и имеющее достаточно большой отрицательный вес, может дать более короткий путь в эту вершину, чем путь в дереве. Этот момент будет рассмотрен в разделе 21.7 (см. рис. 21.28).
На рис. 21.10 показано развертывание SPT при вычислении по алгоритму Дейкстры, а на рис. 21.11 показан рисунок большего ориентированного SPT-дерева. Хотя алгоритм Дейкстры отличается от алгоритма Прима для вычисления MST только выбором приоритета, SPT-деревья обладают характерными особенностями, отличающими их от MST. Их корень расположен в начальной вершине, а все ребра направлены в сторону от корня, тогда как в MST нет ни корня, ни направлений. При использовании алгоритма Прима мы иногда представляем MST-деревья как направленные деревья с корнем, но такие структуры все равно существенно отличаются от SPT (сравните ориентированное изображение на рис. 20.9 с изображением на рис. 21.11). Вообще-то природа SPT отчасти зависит и от выбора начальной вершины (см. рис. 21.12).
Первоначальная реализация Дейкстры, которая годится для насыщенных графов, в точности соответствует алгоритму Прима для вычисления MST. Мы просто заменяем присваивание приоритета P в программе 20.6
P = e->wt()
(вес ребра) на
P = wt[v] + e->wt()
(расстояние от истока до конечной вершины ребра). Это изменение приводит к классической реализации алгоритма Дейкстры: на каждом шаге к SPT добавляется одно ребро, и каждый раз обновляется расстояние до дерева для всех вершин, смежных с конечной вершиной этого ребра. Одновременно просматриваются все вершины, не включенные в дерево, чтобы найти для включения в дерево ребро, конечная вершина которого не принадлежит дереву и находится на минимальном расстоянии от истока.
Лемма 21.3. С помощью алгоритма Дейкстры можно найти любое SPT в насыщенной сети за линейное время.
Доказательство. Как и в случае алгоритма Прима для вычисления MST, после просмотра кода программы 20.6 очевидно, что время выполнения пропорционально V2, т.е. линейно для насыщенных графов. 
В случае разреженных графов возможно усовершенствование. Алгоритм Дейкстры можно рассматривать как обобщенный метод поиска на графе, который отличается от поиска в глубину (DFS), от поиска в ширину (BFS) и от алгоритма Прима для вычисления MST только правилом добавления ребер в дерево. Как и в "Минимальные остовные деревья" , ребра, которые соединяют вершины дерева с вершинами, не включенными в дерево, содержатся в обобщенной очереди, называемой накопителем (fringe). Для реализации этой обобщенной очереди используется очередь с приоритетами и механизм изменения приоритетов, что позволяет объединить в одной реализации алгоритмы DFS, BFS и Прима (см. "Минимальные остовные деревья" ). Эта схема поиска по приоритетам (PFS) включает и алгоритм Дейкстры. То есть замена оператора присваивания P в программе 20.7 на
P = wt[v] + e->wt()
(расстояние от истока до конечной вершины ребра) дает реализацию алгоритма Дейкстры, которая удобна для обработки разреженных графов.
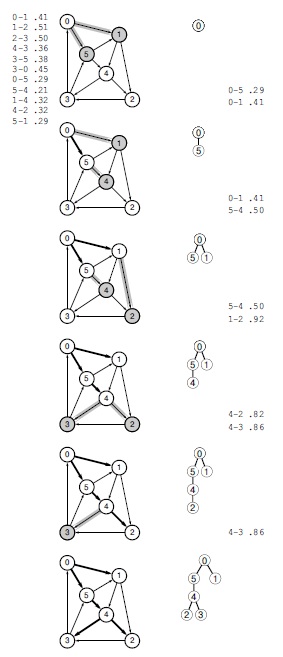
Эта последовательность показывает построение алгоритмом Дейкстры остовного дерева кратчайших путей для сети с корнем в вершине 0. Жирными черными линиями на диаграммах сетей показаны ребра дерева, а жирными серыми - ребра в накопителе. Ориентированные изображения дерева в процессе его роста показаны в центре, а справа приведены списки ребер в накопителе. Вначале в дерево заносится вершина 0, а в накопитель - выходящие из него ребра 0-1 и 0-5 (рисунок вверху). На втором шаге мы переносим самое короткое из этих ребер, 0-5, из накопителя в дерево и проверяем ребра, исходящие из него:ребро 5-4 заносится в накопитель, а ребро 5-1 отбрасывается, поскольку оно не является частью более короткого пути из 0 в 1, чем известный путь 0-1 (второй рисунок сверху). Приоритет ребра 5-4 в накопителе равен длине представленного им пути 0-5-4 из вершины 0. На третьем шаге мы переносим ребро 0-1 из накопителя в дерево, заносим в на-копитель ребро 1-2 и отбрасываем 1-4 (третий сверху рисунок). На четвертом шаге мы переносим 5-4 из накопителя в дерево, заносим в накопитель 4-3 и заменяем 1-2 на 4-2, т.к. путь 0-5-4-2 короче, чем 0-1-2 (четвертый сверху). Мы держим в накопителе не более одного ребра, ведущего к каждой вершине, и выбираем из них то, которое лежит на кратчайшем пути от 0. Вычисление завершается переносом из накопителя в дерево ребра 4-2, а затем 4-3 (рисунок внизу).
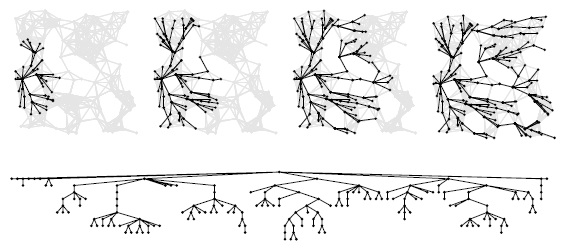
Здесь показана работа алгоритма Дейкстры для решения задачи поиска кратчайших путей из одного истока в случайном евклидовом орграфе с соседними связями (с двунаправленными ребрами, соответствующими каждой начерченной линии) - в том же стиле, что и рис. 18.13, рис. 18.24 и рис. 20.9 Дерево поиска похоже на BFS, т.к. вершины обычно соединяются друг к другом короткими путями, но оно слегка более вытянутое и менее широкое, поскольку использование расстояний приводит к несколько более длинным путям, чем использование длин путей.
Эти три примера демонстрируют рост SPT для трех различных положений истока: левое ребро (вверху), верхний левый угол (в центре), и центр (внизу).
Программа 21.1. Алгоритм Дейкстры (поиск по приоритетам)
Этот класс реализует АТД для поиска кратчайших путей из одного истока с линейным временем предварительной обработки, приватными данными, занимающими объем памяти, пропорциональный V, и функциями-членами с постояннным временем выполнения, которые возвращают длину кратчайшего пути и конечную вершину пути из истока в любую заданную вершину. Конструктор реализует алгоритм Дейкстры, используя для вычисления SPT очередь с приоритетами вершин (в порядке их удаления от истока). Интерфейс очереди с приоритетами - тот же, который используется в программе 20.7 и реализован в программе 20.10.
Конструктор выполняет обобщенный поиск на графе, который реализует другие алгоритмы PFS с другими назначениями приоритета P (см. текст). Оператор обнуления веса вершин дерева необходим для общей реализации PFS, но не для алгоритма Дейкстры, т.к. приоритеты вершин, добавляемых в SPT, являются неубывающими.
template <class Graph, class Edge>
class SPT
{ const Graph &G;
vector<double> wt;
vector<Edge *> spt;
public:
SPT(const Graph &G, int s) : G(G),
spt(G.V()), wt(G.V(), G.V())
{ PQi<double> pQ(G.V(), wt);
for (int v = 0; v < G.V(); v++) pQ.insert(v);
wt[s] = 0.0; pQ.lower(s);
while (!pQ.empty())
{ int v = pQ.getmin(); // wt[v] = 0.0;
if (v != s && spt[v] == 0) return;
typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = А.пх^))
{ int w = e->w();
double P = wt[v] + e->wt();
if (P < wt[w])
{ wt[w] = P; pQ.lower(w); spt[w] = e; }
}
}
}
Edge *pathR(int v) const { return spt[v]; }
double dist(int v) const { return wt[v]; }
};
Программа 21.1 является альтернативной реализацией PFS для разреженных графов; она несколько проще программы 20.7 и непосредственно соответствует неформальному описанию алгоритма Дейкстры в начале этого раздела. Она отличается от программы 20.7 тем, что вначале все вершины сети заносятся в очередь с приоритетами, и те вершины в этой очереди, которые не находятся ни в дереве, ни в накопителе, помечаются сигнальными значениями (невидимые вершины с сигнальными значениями). А программа 20.7 содержит в очереди с приоритетами только вершины, достижимые из дерева через одно ребро. Хранение всех вершин в очереди упрощает код, хотя для некоторых графов может слегка ухудшить эффективность (см. упражнение 21.31).
Общие значения производительности поиска по приоритетам (PFS), рассмотренные в "Минимальные остовные деревья" , дают нам конкретную информацию об эффективности этих реализаций алгоритма Дейкстры для разреженных графов (программа 21.1 и программа 20.7, с соответствующими изменениями). Для удобства мы приведем их еще раз, но уже в текущем контексте. Поскольку доказательства не зависят от функции вычисления приоритета, их можно применить без изменений. Это результаты для наихудшего случая и обеих программ, хотя программа 20.7 может оказаться более эффективной для многих классов графов, поскольку она использует меньший накопитель.
Лемма 21.4. Для всех сетей и всех функций приоритетов можно вычислить остовное дерево с помощью PFS за время, пропорциональное времени, необходимому для выполнения V операций вставить, V операций удалить минимальное и E операций уменьшить ключ в очереди с приоритетами размером не более V.
Доказательство. Этот факт следует непосредственно из реализаций программ 20.7 и 21.1, основанных на очередях с приоритетами. Он дает слишком осторожную верхнюю границу, поскольку размер очереди с приоритетами часто намного меньше V, особенно в программе 20.7. 
Лемма 21.5. С помощью реализации алгоритма Дейкстры на основе PFS, использующей пирамидальное дерево для реализации очереди с приоритетами, можно вычислить любое SPT за время, пропорциональное E lgV.
Доказательство. Этот результат является прямым следствием леммы 21.4. ¦ Лемма 21.6. Пусть задан граф с V вершинами, E ребрами и насыщенностью d = E/V. Если d < 2, то время выполнения алгоритма Дейкстры пропорционально VlgV Иначе реализация очереди с приоритетами на основе 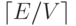 -арного пирамидального дерева позволяет улучшить время выполнения в худшем случае не менее чем в lg(E/V) раз - до
-арного пирамидального дерева позволяет улучшить время выполнения в худшем случае не менее чем в lg(E/V) раз - до 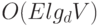 (что линейно, если E равно по крайней мере
(что линейно, если E равно по крайней мере 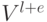 ).
).
Доказательство. Этот результат непосредственно вытекает из леммы 20.12 и реализации очереди с приоритетами на основе многопутевых пирамидальных деревьев, которая рассмотрена после этой леммы. 
В таблице 21.1 сведена информация о рассмотренных нами четырех основных алгоритмах PFS. Они отличаются только используемой функцией вычисления приоритета, но эта разница приводит к совершенно различным остовным деревьям (как и должно быть). Например, на рисунках, упоминаемых в таблице (и для многих других графов), дерево DFS является высоким и узким, дерево BFS - низким и широким; SPT похоже на дерево BFS, но не такое низкое и широкое, а MST - не низкое и широкое, но и не высокое и узкое.
Все эти четыре классических алгоритма обработки графов могут быть реализованы при помощи PFS - т.е. обобщенного поиска на графе, основанного на очереди с приоритетами, который строит остовные деревья, добавляя в них по одному ребру. Детали динамики поиска зависят от представления графа, реализации очереди с приоритетами, а также реализации PFS, однако деревья поиска обычно характеризуют различные алгоритмы (как показано на рисунках, указанных в четвертом столбце).
| Алгоритм | Приоритет | Результат | Рисунок |
|---|---|---|---|
| DFS | Обращение прямого обхода | Дерево рекурсии | 18.13 |
| BFS | Прямой обход | SPT (ребра) | 18.24 |
| Прима | Вес ребра | MST | 20.8 |
| Дейкстры | Вес пути | SPT | 21.9 |
Мы уже рассмотрели четыре различных реализации PFS. Первая - это классическая реализация обхода насыщенного графа, которая охватывает алгоритм Дейкстры и алгоритм Прима для вычисления MST (программа 20.6). Три другие реализации предназначены для разреженных графов и отличаются содержимым очереди с приоритетами:
- Ребра из накопителя (программа 18.10)
- Вершины из накопителя (программа 20.7)
- Все вершины (программа 21.1).
Первая реализация имеет в основном познавательную ценность, вторая наиболее совершенна, а третья, пожалуй, самая простая из всех. На самом деле эта схема описывает 16 различных реализаций классических алгоритмов поиска на графах, а если учесть различные реализации очередей с приоритетами, то возможных вариантов будет еще больше. Это разнообразие сетей, алгоритмов и реализаций подчеркивает важность общих формулировок производительности в леммах 21.4-21.6, которые также сведены в таблицу 21.2.
В этой таблице приведены затраты (время выполнения в худшем случае) различных реализаций алгоритма Дейкстры. При соответствующих реализациях очередей с приоритетами алгоритм выполняется за линейное время (пропорциональное V2 для насыщенных сетей и пропорциональное E для разреженных сетей), за исключением очень разреженных сетей.
| Алгоритм | Трудоемкость в худшем случае | Примечание |
|---|---|---|
| Классический | V2 | Оптимален для насыщенных графов |
| PFS, полное пирамидальное дерево | E lgV | Самая простая реализация |
| PFS, пирамидальное дерево с накопителем | E lgV | Очень осторожная верхняя граница |
| PFS, пирамидальное d-дерево |
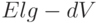
|
Линеен, если граф не слишком разрежен |
Как и в случае алгоритмов вычисления MST, фактическое время поиска кратчайших путей обычно меньше границ для худшего случая - прежде всего потому, что большинство ребер не требуют выполнения операции уменьшить ключ. На практике, за исключением крайне разреженных графов, время выполнения можно считать линейным.
Название алгоритм Дейкстры обычно используется для обозначения как абстрактного метода построения SPT пошаговым добавлением вершин в порядке их расстояния от истока, так и его реализации в виде алгоритма со временем выполнения, пропорциональным V2, для представления матрицей смежности, поскольку Дейкстра представил и то, и другое в своей статье, опубликованной в 1959 г. (а также показал, что этим методом можно вычислить и MST). Повышение производительности на разреженных графах связано с последующими усовершенствованиями в технологии АТД и реализациях очереди с приоритетами, которые не предназначены для задач поиска кратчайших путей. Более высокая производительность алгоритма Дейкстры - одно из наиболее важных свойств этой технологии (см. раздел ссылок). Как и в случае с MST, для указания конкретных сочетаний мы применяем термины вроде " реализация алгоритма Дейкстры на основе PFS с использованием пирамидальных d-деревьев " .
В "Поиск на графе" было показано, что при использовании в невзвешенных неориентированных графах прямой нумерации для приоритетов очередь с приоритетами действует как очередь FIFO и приводит к поиску в ширину (BFS). Алгоритм Дейкстры дает другую реализацию BFS: когда все веса ребер равны 1, он посещает вершины в порядке нумерации ребер на кратчайшем пути к начальной вершине. В этом случае очередь с приоритетами действует не совсем так, как очередь FIFO, т.к. элементы с одинаковыми приоритетами не обязательно извлекаются из очереди в том порядке, в котором они были занесены в нее.
Каждая из этих реализаций помещает ребра SPT-дерева из вершины 0 в индексированный именами вершин вектор spt, а в индексированный именами вершин вектор wt - длины кратчайших путей в каждую вершину SPT, и содержит функции-члены, обеспечивающие клиентам доступ к этим данным. Как обычно, на основе этих первичных данных можно построить различные функции и классы обработки графов (см. упражнения 21.21-21.28).
Упражнения
21.19. Покажите в стиле рис. 21.10 результат вычисления алгоритмом Дейкстры SPT для сети, определяемой в упражнении 21.1, с начальной вершиной 0.
21.20. Как найти второй кратчайший путь в сети из s в t ?
21.21. Напишите клиентскую функцию, которая использует объект SPT для поиска вершины, наиболее удаленной от заданной вершины s (вершина, кратчайший путь в которую из s является наиболее длинным).
21.22. Напишите клиентскую функцию, которая использует объект SPT для вычисления среднего значения длины кратчайших путей из заданной вершины в каждую из вершин, достижимых из нее.
21.23. Разработайте на основе программы 21.1 класс с функцией-членом path, которая возвращает значение типа vector из библиотеки STL, содержащее указатели на ребра кратчайшего пути, соединяющего s и t в направлении от s к t.
21.24. Напишите клиентскую функцию, которая использует класс из упражнения 21.23 для вывода кратчайших путей из заданной вершины в остальные вершины заданной сети.
21.25. Напишите клиентскую функцию, которая использует объект SPT, чтобы найти все вершины, лежащие в пределах заданного расстояния d от заданной вершины в заданной сети. Время выполнения функции должно быть пропорционально размеру подграфа, индуцированного этими и инцидентными им вершинами.
21.26. Разработайте алгоритм поиска ребра, удаление которого вызывает максимальное возрастание длины кратчайшего пути из одной заданной вершины в другую в заданной сети.
21.27. Реализуйте класс, который использует объекты SPT для анализа чувствительности ребер сети по отношению к заданной паре вершин s и t. Вычислите такую матрицу размером V х V, что для каждого u и v элемент на пересечении строки u и столбца v равен 1, если в сети существует ребро u-v, увеличение веса которого не приводит к увеличению длины кратчайшего пути из s в t, и равен 0 в противном случае.
21.28. Реализуйте класс, который использует объекты SPT для поиска кратчайшего пути, соединяющего одно заданное множество вершин с другим заданным множеством вершин в заданной сети.
21.29. Воспользуйтесь решением из упражнения 21.28 для реализации клиентской функции, которая находит кратчайший путь от левого ребра к правому ребру в случайной решетчатой сети (см. упражнение 20.17).
21.30. Покажите, что MST неориентированного графа эквивалентно SPT-дереву критических ребер (bottleneck SPT) этого графа: для каждой пары вершин v и w оно дает соединяющий их путь, наиболее длинное ребро которого имеет минимально возможную длину.
21.31. Эмпирически сравните производительность двух версий алгоритма Дейкстры для разреженных графов, которые описаны в этом разделе (программа 21.1 и программа 20.7, с соответствующим определением приоритета), для различных сетей (см. упражнения 21.4-21.8). Воспользуйтесь реализацией очереди с приоритетами на основе стандартного пирамидального дерева.
21.32. Эмпирически найдите наилучшее значение d для реализации очереди с приоритетами в виде пирамидального d-дерева (см. программу 20.10) для каждой из трех рассмотренных реализаций алгоритма PFS (программы 18.10, 20.7 и 21.1) и для различных сетей (см. упражнения 21.4-21.8).
21.33. Эмпирически определите эффект использования реализации очереди с приоритетами на основе турнира индексного пирамидального дерева (см. упражнение 9.53) в программе 21.1 для различных сетей (см. упражнения 21.4-21.8).
21.34. Эмпирически проанализируйте высоту и среднюю длину пути в SPT для различных сетей (см. упражнения 21.4-21.8).
21.35. Разработайте класс для задачи поиска кратчайших путей из истока в сток, основанный на коде наподобие программы 21.1, но в котором вначале в очередь с приоритетами заносится и исток, и сток. При этом SPT-деревья растут из обеих вершин; ваша основная задача - решить, что делать при их встрече.
21.36. Опишите семейство графов с V вершинами и E ребрами, для которых время работы алгоритма Дейкстры достигает границы для худшего случая.
21.37. Разработайте приемлемый генератор случайных графов с V вершинами и E ребрами, для которых время работы PFS-реализации алгоритма Дейкстры с использованием пирамидального дерева суперлинейно.
21.38. Напишите клиентскую программу для выполнения динамической графической анимации работы алгоритма Дейкстры. Программа должна создавать изображения наподобие рис. 21.11 (см. упражнения 17.56-17.60). Протестируйте программу на случайных евклидовых сетях (см. упражнение 21.9).