Кратчайшие пути
Каждому пути во взвешенном орграфе можно сопоставить вес пути (path weight) - величину, равную сумме весов ребер, составляющих этот путь. Эта важная мера позволяет сформулировать задачи наподобие " найти путь между двумя заданными вершинами, имеющий минимальный вес " . Эти задачи о кратчайших путях (shortest-path problem) и являются темой данной главы. Такие задачи не только естественно возникают во многих приложениях, но и знакомят нас с областью алгоритмов решения общих задач, применимых к широкому кругу реальных приложений.
Некоторые из рассматриваемых в данной главе алгоритмов непосредственно связаны с алгоритмами, изученными в лекциях 17-20. Здесь полностью применима наша базовая парадигма поиска на графе, а в основе решения задач о кратчайших путях лежат некоторые специальные механизмы, которые были использованы в "Виды графов и их свойства" и "Орграфы и DAG-графы" для решения задач связности в графах и орграфах.
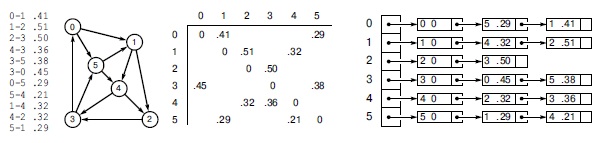
Для краткости мы будем называть взвешенные орграфы сетями (network). На рис. 21.1 показан пример сети и ее стандартные представления. В "Минимальные остовные деревья" уже был разработан интерфейс АТД сети с представлениями матрицей смежности и списками смежности. При вызове конструктора достаточно задать второй аргумент равным true, и класс будет содержать лишь одно представление каждого ребра - как при получении представлений орграфов в "Орграфы и DAG-графы" из представлений неориентированных графов из главы 17 "Виды графов и их свойства" (см. программы 20.1-20.4).
Как было подробно разъяснено в "Минимальные остовные деревья" , при работе со взвешенными орграфами мы используем указатели на абстрактные ребра, чтобы расширить применимость полученных реализаций. У этого подхода для орграфов имеются некоторые отличия по сравнению с неориентированными графами (см. "Минимальные остовные деревья" ). Во-первых, имеется только одно представление каждого ребра, и поэтому при использовании итератора не нужна функция from из класса edge (см. программу 20.1): в орграфе значение e->from(v) истинно для любого указателя на ребро e, возвращаемого итератором для v. Во-вторых, как было показано в "Орграфы и DAG-графы" , часто при обработке орграфа полезно иметь возможность работать с обратным ему графом, но сейчас нам потребуется подход, отличный от принятого в программе 19.1, поскольку там при создании обратного графа создаются ребра, а здесь предполагается, что клиенты АТД графа, предоставляющие указатели на ребра, не должны сами создавать ребра (см. упражнение 21.3).
В приложениях или системах, где могут потребоваться любые типы графов, нетрудно определить такой АТД сети, от которого можно породить АТД для невзвешенных неориентированных графов из глав 17 и 18, невзвешенных орграфов из "Орграфы и DAG-графы" или взвешенных неориентированных графов из "Минимальные остовные деревья" (см. упражнение 21.10).
Здесь показана сеть (взвешенный орграф) и четыре ее представления: список ребер, графический вид, матрица смежности и списки смежности (слева направо). Как и для алгоритмов вычисления MST, веса указываются в элементах матрицы и в узлах списков, но в программах используются указатели на ребра. На рисунках длины ребер часто изображаются пропорциональными их весам (как и для алгоритмов вычисления MST), но мы не настаиваем на этом правиле, поскольку большинство алгоритмов поиска кратчайших путей могут работать с произвольными неотрицательными весами (хотя отрицательные веса могут усложнить ситуацию). Матрица смежности несимметрична, а списки смежности содержат по одному узлу для каждого ребра (как в невзвешенном орграфе). Несуществующие ребра представляются пустыми указателями в матрице (незаполненные места на рисунке) и вообще отсутствуют в списках. Петли нулевой длины введены для упрощения реализации алгоритмов поиска кратчайших путей. Они не представлены в списке ребер слева - для экономии места и чтобы продемонстрировать типичную ситуацию, когда они добавляются при создании представления матрицей смежности или списками смежности.
При работе с сетями обычно удобно оставлять петли во всех представлениях. При таком соглашении для указания, что никакая вершина не достижима из себя самой, в алгоритмах можно использовать сигнальный вес (с максимальным значением). В наших примерах мы будем использовать петли нулевого веса, хотя зачастую имеют смысл петли с положительным весом. Во многих приложениях также требуется наличие параллельных ребер - возможно, с различными весами. Как было сказано в "Минимальные остовные деревья" , в различных приложениях удобны разные варианты игнорирования или объединения таких ребер. Однако в этой главе для простоты ни в одном из наших примеров параллельные ребра не применяются, в представлении матрицей смежности параллельные ребра не допускаются, и мы выполняем проверку наличия параллельных ребер или их удаление в списках смежности.
Все свойства связности ориентированных графов, рассмотренные в "Орграфы и DAG-графы" , справедливы и для сетей. Только там мы выясняли, возможно ли достижение одной вершины из другой, а в этой главе мы учитываем веса и пытаемся найти наилучший путь из одной вершины в другую.
Определение 21.1. Кратчайшим путем между двумя вершинами s и t в сети называется такой направленный простой путь из s в t, что никакой другой путь не имеет меньшего веса.
Лаконичность этого определения скрывает некоторые важные моменты. Во-первых, если t не достижима из s, то не существует вообще никакого пути, поэтому нет и кратчайшего пути. Для удобства рассматриваемые алгоритмы часто трактуют этот случай как наличие между s и t пути с бесконечным весом. Во-вторых, как и в случае алгоритмов вычисления MST, в наших примерах сетей веса ребер пропорциональны их длинам,
хотя определение этого не требует, и в алгоритмах (кроме одного в разделе 21.5) это не предполагается. Вообще-то алгоритмы поиска кратчайшего пути запросто находят неочевидные обходы - например, путь между двумя вершинами, который проходит через несколько других вершин, но имеет общий вес меньше веса ребра, непосредственно соединяющего эти вершины. В-третьих, может существовать несколько путей из одной вершины в другую с одним и тем же весом - обычно достаточно найти один из них. На рис. 21.2 показан пример, иллюстрирующий эти моменты.
В определении требуется, чтобы путь был простым, хотя для сетей, содержащих ребра с неотрицательными весами, это несущественно, поскольку в такой сети можно удалить из пути любой цикл и получить не более длинный путь (даже более короткий, если цикл не состоит из ребер с нулевым весом). Но в случае сетей с ребрами, которые могут иметь отрицательный вес, необходимость ограничиться простыми путями понятна: ведь если в сети есть цикл с отрицательным весом, то понятие кратчайшего пути теряет смысл. Например, предположим, что ребро 3-5 в сети на рис. 21.1 имеет вес -0.38, а ребро 5-1 - вес -0.31. Тогда вес цикла 1-4-3-5-1 равен 0.32 + 0.36 - 0.38 - 0.31 = -0.01. Можно кружить по этому циклу, порождая все более короткие пути. Учтите, что не обязательно, как и в данном примере, чтобы все ребра в таком цикле имели отрицательные веса; значение имеет лишь сумма весов ребер. Для краткости ориентированные циклы с общим отрицательным весом мы будем называть отрицательными циклами.
Предположим, что в определении одна из вершин на пути из s в t принадлежит также некоторому отрицательному циклу. В этом случае существование (непростого) кратчайшего пути из s в t бессмысленно, поскольку можно использовать цикл для создания пути с весом, меньшим любого заданного значения. Чтобы избежать таких моментов, в данном определении мы ограничиваемся простыми путями - тогда понятие кратчайшего пути можно строго определить для любой сети. До раздела 21.7 мы не будем рассматривать отрицательные циклы в сетях, поскольку, как мы увидим, они представляют собой принципиальное препятствие на пути решения задачи поиска кратчайших путей.
Чтобы найти кратчайшие пути во взвешенном неориентированном графе, можно построить сеть с теми же вершинами и с двумя ребрами (по одному в каждом направлении), которые соответствуют каждому ребру в исходном графе.
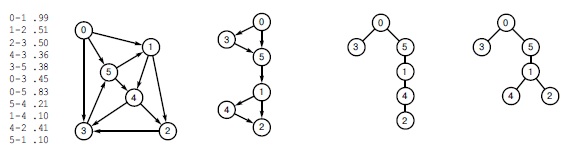
Дерево кратчайших путей (SPT) определяет наиболее короткие пути из корня в другие вершины (см. определение 21.2). В общем случае различные пути могут иметь одинаковую длину, поэтому может существовать несколько SPT, определяющих кратчайшие пути из заданной вершины. В сети, приведенной слева, все кратчайшие пути из 0 являются подграфами DAG-графа, показанного справа от сети. Дерево с корнем в 0 является остовом этого DAG тогда и только тогда, когда оно является SPT-деревом для вершины 0. Два таких дерева приведены справа.
Существует взаимно однозначное соответствие между простыми путями в сети и простыми путями в графе, и стоимости этих путей совпадают; значит, совпадают и задачи поиска кратчайших путей для них. При построении стандартного представления списками смежности или матрицей смежности для взвешенного неориентированного графа (см., например, рис. 20.3) получается точно такая же сеть. Это построение бесполезно, если веса могут быть отрицательными, поскольку в сети при этом получаются отрицательные циклы, а мы не знаем, как решать задачи поиска кратчайших путей в сетях с отрицательными циклами (см. раздел 21.7). В остальных случаях алгоритмы для сетей, которые рассматриваются в этой главе, работают и для взвешенных неориентированных графов.
В некоторых приложениях удобно вместо ребер либо наряду с ребрами присваивать веса вершинам; можно также рассмотреть более сложные задачи, где имеют значение как количество ребер в пути, так и общий вес пути. Подобные задачи можно решать, приводя их к сетям со взвешенными ребрами (см., например, упражнение 21.4) или несколько расширяя базовые алгоритмы (см., например, упражнение 21.52).
Поскольку из контекста и так все понятно, мы не вводим специальную терминологию, позволяющую отличать кратчайшие пути во взвешенных графах от кратчайших путей в графах без весов (где вес пути просто равен количеству составляющих его ребер - см. "Виды графов и их свойства" ). Общепринятая терминология относится к сетям (со взвешенными ребрами), как в данной главе, т.к. особые случаи для неориентированных или невзвешенных графов легко решаются с помощью тех же алгоритмов, что и для сетей.
Мы будем рассматривать те же базовые задачи, которые были определены в "Поиск на графе" для неориентированных и невзвешенных графов. Мы вновь формулируем их здесь, обращая внимание на то, что определение 21.1 неявно обобщает их, учитывая веса в сетях.
Кратчайший путь из истока в сток. Для заданных начальной вершины s и конечной вершины t нужно найти кратчайший путь в графе из s в t. Начальную вершину мы называем истоком (source), а конечную вершину - стоком (sink), за исключением тех ситуаций, где такое использование терминов противоречит другому определению истоков (вершин без входящих ребер) и стоков (вершин без исходящих ребер) в орграфах.
Кратчайшие пути из одного истока. Для заданной начальной вершины s нужно найти кратчайшие пути из s во все остальные вершины графа.
В этой таблице приведены все кратчайшие пути в сети с рис. 21.1 вместе с их длинами. Поскольку данная сеть является сильно связной, в ней существуют пути, соединяющие каждую пару вершин. Цель алгоритма поиска кратчайшего пути из истока в сток - вычисление одного из элементов этой таблицы; цель алгоритма поиска кратчайшего пути из одного истока - вычисление одной из строк этой таблицы; а цель алгоритма поиска кратчайших путей между всеми парами вершин - вычисление всей таблицы. Обычно мы используем более компактные представления, которые содержат по существу ту же информацию и позволяют клиентам обойти любой путь за время, пропорциональное количеству его ребер (см. рис. 21.8).
Кратчайшие пути между всеми парами вершин. Нужно найти кратчайшие пути, соединяющие каждую пару вершин в графе. Иногда для краткости это множество V2 путей мы будем называть термином все кратчайшие пути.
Если имеется несколько кратчайших путей, соединяющих любую заданную пару вершин, мы выбираем любой из них. Поскольку пути имеют различное количество ребер, наши реализации предоставляют функции-члены, которые позволяют клиентам обходить пути за время, пропорциональное длинам путей. Любой кратчайший путь неявно содержит и собственную длину, но наши реализации выдают длины явно. Итак, уточним: в приведенных выше постановках задач выражение " найти кратчайший путь " означает " вычислить длину кратчайшего пути и способ обхода конкретного пути за время, пропорциональное его длине " .
На рис. 21.3 показаны кратчайшие пути для сети с рис. 21.1. В сетях с V вершинами для решения задачи с одним истоком необходимо указать V путей, а для решения задачи для всех пар вершин - V2 путей. В наших реализациях мы используем более компактное представление, чем эти списки путей; об этом уже было упомянуто в "Поиск на графе" и будет подробно рассказано в разделе 21.1.
В реализациях на C++ мы строим алгоритмические решения этих задач в виде реализаций АТД, позволяющих создавать эффективные клиентские программы, которые могут решать разнообразные практические задачи обработки графов. Например, как показано в разделе 21.3, мы реализуем решения задач кратчайших путей для всех пар вершин в виде конструкторов внутри классов, которые отвечают на запросы кратчайшего пути за постоянное (линейное) время. Мы также построим классы для решения задачи с одним истоком, чтобы клиенты, которым нужно вычислить кратчайшие пути из заданной вершины (или небольшого множества вершин) могли не вычислять кратчайшие пути для других вершин. Внимательное рассмотрение таких моментов и надлежащее использование изучаемых здесь алгоритмов может преодолеть разницу между эффективным решением и настолько трудоемким решением, что никакой клиент не сможет воспользоваться им.
Задачи о кратчайших путях в различных вариантах возникают в широком спектре приложений. Многие приложения допускают наглядную геометрическую интерпретацию, но многие другие обрабатывают структуры с произвольными стоимостями. Как и в случае минимальных остовных деревьев (MST, см. "Минимальные остовные деревья" ), мы иногда будем обращаться к геометрической интерпретации, чтобы облегчить понимание алгоритмов решения этих задач - постоянно помня, что наши алгоритмы способны работать и в более общих условиях. В разделе 21.5 мы рассмотрим специализированные алгоритмы для евклидовых сетей. А в разделах 21.6 и 21.7 будет показано, что базовые алгоритмы эффективны для многочисленных приложений, в которых сети представляют абстрактную модель вычислений.
Дорожные карты. Во многих дорожных картах есть замечательная вещь - таблицы с расстояниями между всеми парами главных городов. Мы считаем, что составитель карты позаботился о том, чтобы эти расстояния кратчайшими, но это предположение не всегда верно (см., например, упражнение 21.11). Обычно такие таблицы составляются для неориентированных графов, которые можно рассматривать как сети с двунаправленными ребрами, соответствующими каждой дороге, хотя в них можно включать улицы с односторонним движением на карте города и некоторые другие аналогичные моменты. Как будет показано в разделе 21.3, нетрудно предоставлять и другую полезную информацию - например, таблицу с инструкцией о прохождении кратчайших путей (см. рис. 21.4). Современные встроенные системы в автомобилях и других транспортных системах предоставляют такие возможности. Карты являются евклидовыми графами, и в разделе 21.4 мы рассмотрим алгоритмы поиска кратчайших путей, которые при поиске кратчайших путей учитывают позицию вершины.
Авиарейсы. Карты маршрутов и расписания для авиалиний или других транспортных систем могут быть представлены в виде сетей, для которых важны различные задачи о кратчайших путях. Например, может потребоваться минимизировать время перелета между двумя городами, или же стоимость путешествия. Стоимости в таких сетях могут включать функции от времени, финансовых затрат или других интегральных ресурсов. Например, из-за преобладающих ветров перелеты между двумя городами обычно занимают больше времени в одном направлении, чем в другом. Авиапассажиры также знают, что стоимость перелета не обязательно является простой функцией расстояния между городами - очень часто встречаются ситуации, когда окольный маршрут (с пересадками) дешевле прямого перелета. Такие усложнения могут быть обработаны базовыми алгоритмами поиска кратчайших путей, которые мы рассматриваем в этой главе; эти алгоритмы предназначены для работы с любыми положительными стоимостями.
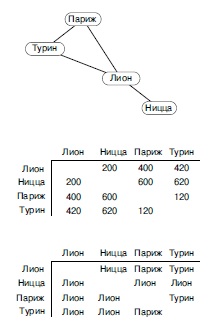
Дорожные карты обычно содержат таблицы расстояний наподобие приведенной в центрери-сунка для небольшого подмножества французских городов. Соединяющие их автострады показаны в виде графа в верхней части рисунка. Может быть полезна, хотя и редко встречается на картах, таблица наподобие приведенной внизу: в ней отмечены пункты, лежащие на кратчайшем пути. Например, из этой таблицы видно, как добраться из Парижа в Ниццу: первым на пути следования должен быть Лион.
Фундаментальные вычисления кратчайших путей, предлагаемые этими приложениями - это лишь небольшая часть области применимости алгоритмов для вычисления кратчайших путей. В разделе 21.6 мы рассмотрим задачи из прикладных областей, которые с виду не имеют отношения к данной тематике. В этом нам поможет сведение - формальный механизм для доказательства связи между задачами. Мы решаем задачи для этих приложений, трансформируя их в абстрактные задачи поиска кратчайших путей, которые не имеют очевидной геометрической связи с описанными задачами. Некоторые приложения приводят к задачам о кратчайших путях в сетях с отрицательными весами. Такие задачи могут оказаться намного более трудными, чем задачи, где отрицательные веса невозможны. Задачи о кратчайших путях для таких приложений не только заполняют промежуток между элементарными алгоритмами и алгоритмически неразрешимыми задачами, но и приводят нас к мощным и общим механизмам принятия решений.
Как и в случае алгоритмов вычисления MST из "Минимальные остовные деревья" , мы часто смешиваем понятия веса, стоимости и расстояния. Здесь мы обычно также используем естественную геометрическую наглядность, даже работая с более общими постановками и с произвольными весами ребер. Поэтому мы говорим о " длине " путей и ребер вместо " веса " , и говорим, что один путь " короче " другого, вместо выражения " имеет меньший вес " . Мы также можем сказать, что вершина v находится " ближе " к s, чем w, вместо " ориентированный путь наименьшего веса из s в v имеет меньший вес, чем вес ориентированного пути наименьшего веса из s в w " , и т.д. Это проявляется и в стандартном использовании термина " кратчайшие пути " и выглядит естественно, даже если веса не связаны с расстояниями (см. рис. 21.2). Однако в разделе 21.6, при расширении наших алгоритмов на отрицательные веса, от этого придется отказаться.
Эта глава организована следующим образом. После знакомства с фундаментальными принципами в разделе 21.1, в разделах 21.2 и 21.3 мы рассмотрим базовые алгоритмы для задач поиска кратчайших путей из одного истока и между всеми парами вершин. После этого в разделе 21.4 мы изучим ациклические сети (или, короче, взвешенные DAG-графы), а в разделе 21.5 - методы использования геометрических свойств для решения задачи с одним истоком и стоком в евклидовых графах. Затем в разделах 21.6 и 21.7 мы переключимся на более общие задачи, где алгоритмы поиска кратчайших путей (возможно, на сетях с отрицательными весами) будут использованы как высокоуровневое средство решения задач.
Упражнения
21.1. Пометьте следующие точки на плоскости цифрами от 0 до 5, соответственно:
(1, 3) (2, 1) (6, 5) (3, 4) (3, 7) (5, 3).
Считая длины ребер весами, рассмотрите сеть, определяемую ребрами
1-03-55-23-45-10-30-44-22-3.
Нарисуйте сеть и приведите структуру списков смежности, которая формируется программой 20.5.
21.2. Покажите в стиле рис. 21.3 все кратчайшие пути в сети, определенной в упражнении 21.1.
21.3. Разработайте реализацию класса сети, который представляет обращение взвешенного орграфа, который определяется вставленными ребрами. Включите в реализацию конструктор " обратного копирования " , который принимает в качестве аргумента граф и использует все ребра этого графа для построения обращения.
21.4. Покажите, что для вычисления кратчайших путей в сетях с неотрицательными весами и в вершинах, и на ребрах (где вес пути определяется как сумма весов вершин и ребер на этом пути), достаточно построения АТД сети с весами только на ребрах.
21.5. Найдите в инернете какую-либо доступную большую сеть, содержащую расстояния или стоимости - возможно, географическую базу данных с информацией о дорогах, соединяющих города, либо расписания движения самолетов или поездов.
21.6. Напишите генератор разреженных случайных сетей на основе программы 17.12. Для присваивания весов ребрам определите АТД ребер случайного веса и напишите две реализации: одну для генерации равномерно распределенных весов, а другую - для нормально распределенных. Напишите клиентские программы, генерирующие разреженные случайные сети для обоих распределений весов с таким множеством значений V и E, чтобы их можно было использовать для выполнения эмпирических тестов на графах.
21.7. Напишите генератор насыщенных случайных сетей на основе программы 17.13 и генератора ребер случайного веса из упражнения 21.6. Напишите клиентские программы, генерирующие случайные сети для обоих распределений весов с таким множеством значений V и E, чтобы их можно было использовать для выполнения эмпирических тестов на графах.
21.8. Реализуйте независимую от представления сети клиентскую функцию, которая строит сеть, получая ребра с весами (пары целых чисел из диапазона от 0 до V- 1 с весами от 0 до 1) из стандартного ввода.
21.9. Напишите программу, которая генерирует V случайных точек на плоскости, затем строит сеть с (двунаправленными) ребрами, соединяющими все пары точек, расстояние между которыми не превышает заданное значение d (см. упражнение 17.74), и устанавливает вес каждого ребра равным расстоянию между концами этого ребра. Определите, каким должно быть d, чтобы ожидаемое количество ребер было равно E.
21.10. Напишите базовый класс и производные классы, реализующие абстрактные типы данных для графов, которые могут быть неориентироваными или ориентированными, взвешенными или невзвешенными и насыщенными или разреженными.
21.11. Приведенная ниже таблица из опубликованной дорожной карты содержит длины кратчайших маршрутов, соединяющих города. Найдите в таблице ошибку и исправьте ее. Составьте также таблицу в стиле рис. 21.4, которая показывает, как проследовать по кратчайшему маршруту.