Кратчайшие пути

Кратчайшие пути в ациклических сетях

В "Орграфы и DAG-графы" мы обнаружили, что вопреки нашим ожиданиям, что обработка DAG-графов должна быть проще, чем обработка обычных орграфов, разработка алгоритмов с существенно большей скоростью работы для DAG-графов по сравнению с обычными орграфами является труднодостижимой целью. Однако в случае задач о кратчайших путях действительно существуют алгоритмы для DAG, которые проще и быстрее, чем методы на основе очереди с приоритетами для обычных орграфов. В частности, в этом разделе мы рассмотрим алгоритмы для ациклических сетей, которые:

• Решают задачу для одного истока за линейное время.
• Решают задачу для всех пар вершин за время, пропорциональное VE.
• Решают другие задачи, например, поиск наиболее длинных путей.

В первых двух случаях мы устраняем из времени выполнения логарифмический множитель, который присутствует в наших лучших алгоритмах для разреженных сетей; в третьем случае имеются простые алгоритмы решения задач, которые трудноразрешимы для сетей общего вида. Все эти алгоритмы являются прямыми расширениями алгоритмов решения задач достижимости и транзитивного замыкания для DAG-графов, которые рассматривались в "Орграфы и DAG-графы" .

Поскольку в ациклических сетях нет циклов вообще, то нет и отрицательных циклов, поэтому отрицательные веса не вызывают трудностей в задачах поиска кратчайших путей на DAG-графах. Соответственно, в материале этого раздела мы не накладываем ограничения на значения весов ребер.

Есть одно замечание, касающееся терминологии: ориентированные графы с весами на ребрах и без циклов можно называть либо взвешенными DAG, либо ациклическими сетями.

Мы будем применять оба термина - как для того, чтобы подчеркнуть их эквивалентность, так и для того, чтобы избежать путаницы при обращении к литературе, где широко используются оба термина. Иногда удобно использовать первый из них, чтобы обратить внимание на отличие от невзвешенного DAG (взвешенность), а второй - чтобы подчеркуть отличие от обычных сетей (ацикличность).

Четыре базовых концепции из "Орграфы и DAG-графы" , которые позволили получить эффективные алгоритмы для невзвешенных DAG-графов, оказываются даже более эффективными для взвешенных DAG:

• Использование DFS для решения задачи с одним истоком.
• Использование очереди истоков для решения задачи с одним истоком.
• Вызов любого метода один раз для каждой вершины при решении задачи для всех пар вершин.
• Использование одного DFS (с динамическим программированием) при решении задачи для всех пар вершин.

Эти методы решают задачу с одним истоком за время, пропорциональное E, и задачу для всех пар вершин - за время, пропорциональное VE. Все они эффективны в силу топологического упорядочения, которое позволяет вычислять кратчайшие пути для каждой вершины без перепроверки предыдущих решений. В этом разделе мы рассмотрим по одной реализации для каждой задачи; остальные оставлены читателям на самостоятельную проработку (см. упражнения 21.62-21.65).

Начнем с небольшого отступления. Каждый DAG имеет по крайней мере один исток, а может, и несколько, поэтому вполне естественно рассмотреть следующую задачу о кратчайших путях.

Кратчайшие пути из нескольких истоков. При заданном наборе начальных вершин для каждой из остальных вершин w нужно найти самый короткий путь среди всех кратчайших путей из каждой начальной вершины до w.

Эта задача по существу эквивалентна задаче о кратчайших путях из одного истока. Задачу для нескольких истоков можно свести к задаче для одного истока, добавив фиктивную вершину-исток с ребрами нулевой длины, ведущими в каждый исток исходной сети. Можно и наоборот: свести задачу с одним истоком к задаче с несколькими истоками; для этого нужно рассмотреть подсеть, индуцированную всеми вершинами и ребрами, достижимыми из исходного истока. Мы редко создаем такие подсети явно, поскольку наши алгоритмы обрабатывают их автоматически, когда мы считаем начальную вершину единственным истоком в сети (даже если это не так).

Топологическая сортировка позволяет непосредственно решить задачу кратчайших путей с несколькими истоками и множество других задач. Мы используем индексированный именами вершин вектор wt, который содержит веса известных кратчайших путей из любого истока в каждую вершину. Чтобы решить задачу поиска кратчайших путей с несколькими истоками, мы вначале заносим в вектор wt нулевые значения для истоков и большое сигнальное значение для всех остальных вершин. Затем мы обрабатываем эти вершины в топологическом порядке. Чтобы обработать вершину v, для каждого исходящего из нее ребра v-w мы выполняем операцию релаксации, которая обновляет кратчайший путь в w, если v-w дает более короткий путь из истока в w (через v). В процессе выполнения этих операций проверяются все пути из любого истока в каждую вершину графа; операция релаксации отслеживает минимальную длину таких путей, а топологическая сортировка гарантирует обработку вершин в нужном порядке.

Этот метод можно реализовать непосредственно одним из двух способов. Первый заключается в добавлении нескольких строк кода к коду топологической сортировки в программе 19.8: сразу после извлечения из исходной очереди вершины v мы выполняем для каждого из ее ребер указанную операцию релаксации (см. упражнение 21.56). Второй способ - топологическое упорядочение вершин и последующий проход по ним с выполнением операций релаксации так, как описано в предыдущем абзаце.

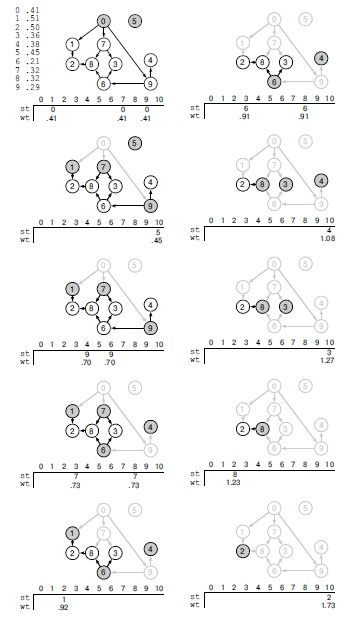
Подобным же образом (с другими операциями релаксации) можно решить многие задачи обработки графов. Например, программа 21.6 представляет собой реализацию второго подхода (упорядочение с последующим просмотром) для решения задачи поиска наиболее длинных путей из нескольких истоков: для каждой вершины сети нужно найти наиболее длинный путь из некоторого истока в эту вершину. При этом элемент wt, связанный с каждой вершиной, содержит длину самого длинного известного пути из любого истока в эту вершину, вначале мы обнуляем все веса и изменяем смысл сравнения в операции релаксации. На рис. 21.15 показана трасса выполнения программы 21.6 на примере ациклической сети.

Программа 21.6. Наиболее длинные пути в ациклической сети

Для нахождения наиболее длинных путей в ациклической сети мы рассматриваем вершины в топологическом порядке, и, выполняя для каждого ребра шаг релаксации, сохраняем в индексированном именами вершин векторе wt вес наиболее длинного известного пути в каждую вершину. Вектор lpt определяет остовный лес наиболее длинных путей (с корнями в истоках), а вызов path(v) возвращает последнее ребро в наиболее длинном пути, ведущем в v.

  #include "dagTS.cc"
  template <class Graph, class Edge>
  class LPTdag
    {
      const Graph &G;
      vector<double> wt;
      vector<Edge *> lpt;
    public:
      LPTdag(const Graph &G) : G(G), lpt(G.V()), wt(G.V(), 0)
        {
          int j, w;
          dagTS<Graph> ts(G);
          for (int v = ts[j = 0]; j < G.V(); v = ts[++j])
            {
              typename Graph::adjIterator A(G, v);
              for (Edge* e = A.beg(); !A.end(); e = A.nxt())
                if (wt[w = e->w()] < wt[v] + e->wt())
                  {
                    wt[w] = wt[v] + e->wt();
                    lpt[w] = e;
                  }
            }
        }
    Edge *pathR(int v) const { return lpt[v]; }
    double dist(int v) const { return wt[v]; }
    } ;
      

Рис. 21.15. Вычисление наиболее длинных путей в ациклической сети

В этой сети каждое ребро имеет вес, связываемый с его исходной вершиной (их список приведен вверху слева). У стоков есть ребра в фиктивную вершину 10, которая на рисунках не показана. Массив wt содержит длину наиболее длинного известного пути в каждую вершину из некоторого истока, а массив st хранит предыдущую вершину на наиболее длинном пути. Этот рисунок иллюстрирует действие программы 21.6, которая выбирает один из истоков (затененные узлы на каждой диаграмме) по правилу FIFO, хотя на каждом шаге можно выбирать любые истоки. Вначале мы извлекаем вершину 0, просматриваем каждое инцидентное ей ребро и обнаруживаем однореберные пути длины 0.41, ведущие в 1, 7 и 9. Затем мы извлекаем вершину 5 и записываем однореберный путь из 5 в 10 (слева, второй ряд сверху). Потом извлекаем вершину 9 и записываем пути 0-9-4 и 0-9-6 длины 0.70 (слева, третий ряд сверху). Мы продолжаем эти действия, изменяя массивы каждый раз, когда находим более длинные пути. Например, после извлечения вершины 7 (слева, второй ряд снизу) мы записываем пути длины 0.73, ведущие в 8 и 3; затем, после извлечения вершины 6, мы записываем более длинные пути (длины 0.91) в 8 и 3 (справа вверху). Цель вычислений - найти наиболее длинный путь к фиктивному узлу 10. В данном случае результатом является путь 0-9-6-8-2 длины 1.73.

Эта важная лемма говорит нам, что обработка ациклических сетей выполняется значительно проще, чем обработка сетей с циклами. Для кратчайших путей этот способ быстрее алгоритма Дейкстры на коэффициент, пропорциональный стоимости операций обработки очереди с приоритетами в алгоритме Дейкстры. В случае задачи о наиболее длинных путях мы получаем линейный алгоритм для ациклических сетей, но трудноразрешимую задачу в случае сетей общего вида. Кроме того, здесь отрицательные веса не представляют дополнительной трудности, однако являются труднопреодолимым барьером в алгоритмах для сетей общего вида, о чем будет сказано в разделе 21.7.

Описанный метод зависит только от того факта, что вершины обрабатываются в топологическом порядке. Следовательно, любой алгоритм топологической сортировки можно адаптировать для решения задач о кратчайших и наиболее длинных путях и других задач этого типа (см., например, упражнения 21.56 и 21.62).

Как мы знаем из "Орграфы и DAG-графы" , абстракция DAG используется во многих приложениях. Например, в разделе 21.6 мы увидим приложение, которое с виду не связано с сетями, но для которого можно непосредственно задействовать программу 21.6.

А теперь мы переходим к задаче о кратчайших путях для всех пар вершин в ациклических сетях. Как и в "Орграфы и DAG-графы" , один из методов решения этой задачи - выполнение алгоритма для одного истока для каждой вершины (см. упражнение 11.65). Не менее эффективный подход, который мы рассмотрим здесь, заключается в применении единственного DFS с динамическим программированием, как при вычислении транзитивного замыкания DAG в "Орграфы и DAG-графы" (см. программу 19.9). Если рассматривать вершины в конце выполнения рекурсивной функции, то они будут обрабатываться в обратном топологическом порядке, и мы сможем получить вектор кратчайших путей для каждой вершины из векторов кратчайших путей для каждой смежной вершины, просто используя каждое ребро на шаге релаксации.

Программа 21.7 является реализацией этого подхода. Работа данной программы на примере взвешенного DAG показана на рис. 21.16. Кроме добавления релаксации, имеется одно важное различие между этим вычислением и вычислением транзитивного замыкания для DAG: в программе 19.9 можно игнорировать ребра в дереве DFS, которые не несут новой информации о достижимости, а в программе 21.7 приходится рассматривать все ребра, поскольку любое ребро может привести к более короткому пути.

Программа 21.7. Все кратчайшие пути в ациклической сети

Эта реализация интерфейса из программы 21.2 для взвешенного DAG получена добавлением соответствующих операций релаксации в функцию транзитивного замыкания из программы 19.9, основанной на динамическом программировании.

  template <class Graph, class Edge>
  class allSPdag
    { const Graph &G;
      vector <vector <Edge *> > p;
      vector <vector <double> > d;
      void dfsR(int s)
        { typename Graph::adjIterator A(G, s);
          for (Edge* e = A.beg(); !A.end(); e = A.nxt())
            { int t = e->w(); double w = e->wt();
              if ( d[s][t] > w)
                { d[s][t] = w; p[s][t] = e; }
              if (p[t][t] == 0) dfsR(t);
              for (int i = 0; i < G.V(); i++)
                if (p[t][i])
                  if (d[s][i] > w + d[t][i])
                    { d[s][i] = w + d[t][i]; p[s][i] = e; }
            }
        }
    public:
      allSPdag(const Graph &G) : G(G), p(G.V()), d(G.V())
        { int V = G.V();
          for (int i = 0; i < V; i++)
            { p[i].assign(V, 0); d[i].assign(V, V); }
          for (int s = 0; s < V; s++)
            if (p[s][s] == 0) dfsR(s);
        }
       Edge *path(int s, int t) const
        { return p[s][t]; }
       double dist(int s, int t) const
        { return d[s][t]; }
    } ;
      

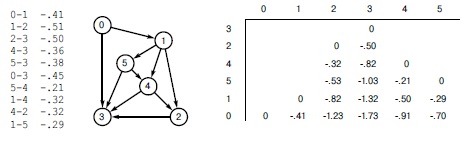
Таким образом, топологическая сортировка для ациклических сетей позволяет избежать затрат на работу очереди с приоритетами в алгоритме Дейкстры. Подобно алгоритму Флойда, программа 21.7 также решает задачи, более общие, чем те, которые решаются алгоритмом Дейкстры, т.к., в отличие от алгоритма Дейкстры (см. раздел 21.7), этот алгоритм работает правильно даже при наличии ребер с отрицательными весами. Если изменить знаки всех весов в ациклической сети, то этот алгоритм найдет все наиболее длинные пути (см. рис. 21.17). Наиболее длинные пути можно найти и по-другому - изменив проверку неравенства в алгоритме релаксации, как в программе 21.6.

Остальные алгоритмы поиска кратчайших путей в ациклических сетях, которые были упомянуты в начале этого раздела, обобщают методы из "Орграфы и DAG-графы" подобно другим алгоритмам, которые рассматривались в этой главе. Их самостоятельная реализация позволит закрепить ваше понимание как DAG-графов, так и кратчайших путей (см. упражнения 21.62-21.65). Все эти методы выполняются в худшем случае за время, пропорциональное VE, а реальная трудоемкость зависит от структуры DAG. В принципе, для некоторых разреженных взвешенных DAG-графов можно привести даже лучшую оценку (см. упражнение 19.117).

Рис. 21.16. Кратчайшие пути в ациклической сети

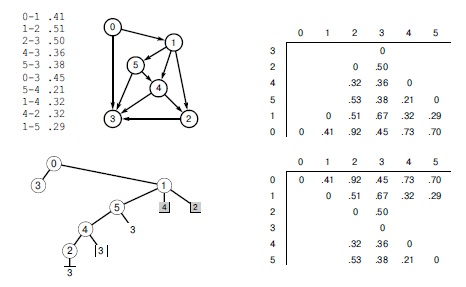
Здесь показано вычисление матрицы всех кратчайших расстояний (внизу справа) для примера взвешенного DAG (вверху слева). Каждая строка этой матрицы вычисляется последним действием рекурсивной функции DFS из строк для смежных вершин, которые находятся раньше в списке, поскольку строки вычисляются в обратном топологическом порядке (обратный обход дерева DFS, которое изображено внизу слева).

Массив вверху справа содержит строки матрицы в порядке их вычисления. Например, чтобы вычислить каждый элемент строки для вершины 0, мы добавляем 0.41 к соответствующему элементу в строке для вершины 1 (чтобы получить расстояние до нее из 0 после рассмотрения ребра 0-1), затем добавляем 0.45 к соответствующему элементу в строке для вершины 3 (чтобы получить расстояние до нее из 0 после рассмотрения 0-3), а затем выбираем меньшее из этих двух значений. Эти вычисления по сути совпадают с вычислением транзитивного замыкания DAG (см., например, рис. 19.23). Наиболее значительное различие состоит в том, что алгоритм вычисления транзитивного замыкания может игнорировать некоторые ребра (например, 1-2 в этом примере), поскольку они ведут к вершинам, достижимость которых уже установлена; а алгоритм кратчайших путей должен проверять, являются ли пути, связываемые с нисходящими ребрами, более короткими, чем уже известные пути. Если игнорировать ребро 1-2 в этом примере, то не будут найдены кратчайшие пути 0-1-2 и 1-2.

Рис. 21.17. Все наиболее длинные пути в ациклической сети

Наш метод для вычисления всех кратчайших путей в ациклических сетях работает даже при наличии отрицательных весов. Поэтому он позволяет вычислить наиболее длинные пути: для этого нужно вначале изменить знаки всех весов, как показано здесь для сети с рис. 21.16. Наиболее длинным простым путем в этой сети является 0-1-5-4-2-3 с весом 1.73 .

Упражнения

21.54. Приведите решения задач поиска кратчайших и наиболее длинных путей с несколькими истоками для сети, определенной в упражнении 21.1, с обращенными направлениями ребер 2-3 и 1-0.

21.55. Измените программу 21.6, чтобы она решала задачу поиска кратчайших путей с несколькими истоками для ациклических сетей.

21.56. Реализуйте класс с тем же интерфейсом, что и в программе 21.6, на основе кода топологической сортировки с очередью истоков из программы 19.8, который выполняет операцию релаксации для каждой вершины сразу после извлечения этой вершины из очереди истоков.

21.57. Определите АТД для операции релаксации, напишите его реализацию и измените программу 21.6 так, чтобы полученный АТД можно было использовать аналогично программе 21.6 для решения задачи о кратчайших путях с несколькими истоками, задачи о наиболее длинных путях с несколькими истоками и других задач, просто измененяя реализацию операции релаксации.

21.58. Воспользуйтесь обобщенной реализацией из упражнения 21.57 для разработки класса с функциями-членами, которые возвращают длину наиболее длинного пути из любого истока в любую другую вершину DAG, длину кратчайшего такого пути и количество вершин, достижимых путями, длины которых принадлежат заданному интервалу.

21.59. Определите свойства релаксации, чтобы изменить доказательство леммы 21.9 для абстрактной версии программы 21.6 (наподобие описанной в упражнении 21.57).

21.60. Продемонстрируйте в стиле рис. 21.16 вычисление матриц кратчайших путей для всех пар вершин в сети, определенной в упражнении 21.54, с помощью программы 21.7.

о 21.61. Приведите верхнюю границу количества весов ребер, просмотренных в программе 21.7, в виде функции базовых структурных свойств сети. Напишите программу вычисления этой функции и воспользуйтесь ей для оценки точности границы VE в различных ациклических сетях (добавьте нужные веса в моделях из "Орграфы и DAG-графы" ).

21.62. Напишите основанное на DFS решение задачи о кратчайших путях с несколькими истоками для ациклических сетей. Будет ли это решение правильно работать при наличии отрицательных весов ребер? Обоснуйте свой ответ.

21.63. Расширьте решение упражнения 21.62, чтобы получить реализацию интерфейса АТД кратчайших путей для всех пар вершин для ациклических сетей, которая формирует матрицы всех путей и всех расстояний за время, пропорциональное VE.

21.64. Продемонстрируйте в стиле рис. 21.9 вычисление всех кратчайших путей в сети, определенной в упражнении 21.54, с помощью метода на основе DFS из упражнения 21.63.

21.65. Измените программу 21.6, чтобы она решала задачу поиска кратчайших путей из одного истока в ациклических сетях, а затем используйте ее для разработки реализации интерфейса АТД кратчайших путей для всех пар вершин в ациклических сетях, который формирует матрицы всех путей и всех расстояний за время, пропорциональное VE.

21.66. Выполните упражнение 21.61 для реализации АТД кратчайших путей для всех пар вершин на основе DFS (упражнение 21.63) и на основе топологической сортировки (упражнение 21.65). Какие выводы можно сделать, сравнивая трудоемкости этих трех методов?

21.67. Эмпирически сравните в стиле таблицы 20.2 три реализации класса для задачи поиска кратчайших путей для всех пар вершин, описанные в этом разделе (см. программу 21.7, упражнение 21.63 и упражнение 21.65), для различных ациклических сетей (добавьте нужные веса в моделях из "Орграфы и DAG-графы" ).