Кратчайшие пути

Кратчайшие пути между всеми парами вершин

В этом разделе мы рассмотрим два класса, решающие задачу поиска кратчайших путей для всех пар вершин. Алгоритмы, которые мы реализуем, непосредственно обобщают два базовых алгоритма, которые были рассмотрены в "Орграфы и DAG-графы" для задачи транзитивного замыкания. Первый метод заключается в выполнении алгоритма Дейкстры из каждой вершины для получения кратчайших путей из этой вершины во все остальные. Если реализовать очередь с приоритетами с помощью пирамидального дерева, то при таком подходе время выполнения в худшем случае будет пропорционально VE lgV, а использование d-арного пирамидального дерева позволяет улучшить эту границу для многих типов сетей до VE. Второй метод, который позволяет напрямую решить данную задачу за время, пропорциональное V³, является расширением алгоритма Уоршалла, и называется алгоритм Флойда (Floyd).

Оба класса реализуют интерфейс АТД абстрактных кратчайших путей для нахождения кратчайших расстояний и путей. Этот интерфейс, который показан в программе 21.2, является обобщением интерфейса абстрактного транзитивного замыкания взвешенного орграфа для выяснения связности в орграфах, который был изучен в "Орграфы и DAG-графы" . В реализациях обоих классов конструктор решает задачу поиска кратчайших путей для всех пар вершин и сохраняет результат в приватных членах данных. Эти данные используются функциями ответов на запросы, которые возвращают длину кратчайшего пути из одной заданной вершины в другую, а также первое или последнее ребро в пути. Основное назначение реализации такого АТД - его практическое использование для реализации алгоритмов поиска кратчайших путей для всех пар вершин.

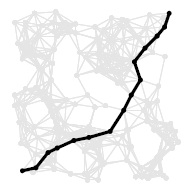
Программа 21.3 представляет собой пример клиентской программы, которая вычисляет взвешенный диаметр (weighted diameter) сети с помощью интерфейса АТД для поиска всех кратчайших путей. Она просматривает все пары вершин и находит такую пару, для которой длина кратчайшего пути максимальна, а затем обходит путь, ребро за ребром. На рис. 21.13 показан путь, вычисленный этой программой для нашей демонстрационной евклидовой сети.

Программа 21.2. АТД кратчайших путей для всех пар вершин

Все наши решения задачи поиска кратчайших путей для всех пар вершин имеют вид классов с конструктором и двумя функциями ответов на запросы. Первая функция, dist, возвращает длину кратчайшего пути из первого аргумента во второй, а вторая - одна из двух возможных функций вычисления пути: либо path, возвращающая указатель на первое ребро в кратчайшем пути, либо pathR, возвращающая указатель на последнее ребро в кратчайшем пути. Если такой путь не существует, то функция path возвращает 0, а результат dist не определен.

Мы используем функции path или pathR в зависимости от того, что удобнее для рассматриваемого алгоритма; возможно, на практике одну из них (или обе) следует поместить в интерфейс, а в реализациях использовать различные вспомогательные функции, как описано в разделе 21.1 и в упражнениях в конце этого раздела.

  template <class Graph, class Edge> class SPall
    { public:
      SPall(const Graph &);
      Edge *path(int, int) const;
      Edge *pathR(int, int) const;
      double dist(int, int) const;
    };
      

Цель алгоритмов, представленных в этом разделе, состоит в обеспечении постоянного времени выполнения функций ответов на запросы. Обычно ожидается огромное количество таких запросов, поэтому лучше затратить значительно больше ресурсов на вычисление приватных членов данных и предварительную обработку в конструкторе, чтобы затем быстро отвечать на запросы. Оба рассматриваемых нами алгоритма требуют объем памяти для приватных членов данных, пропорциональный V².

Рис. 21.13. Диаметр сети

Диаметр сети - это наибольший элемент в матрице всех кратчайших путей сети, т.е. длина наиболее длинного из кратчайших путей, показанного здесь для нашей демонстрационной евклидовой сети.

Основной недостаток этого общего подхода состоит в том, что для огромной сети может не хватить объема доступной памяти (или времени, необходимого на предварительную обработку). В принципе, наш интерфейс позволяет выбирать между затратами времени и памяти на предварительную обработку и затратами памяти при ответе на запрос.

Если ожидается лишь несколько запросов, то можно обойтись без предварительной обработки, и просто выполнять для каждого запроса алгоритм для одного истока; однако в наиболее распространенных ситуациях нужны более совершенные алгоритмы (см. упражнения 21.48-21.50). Эта задача обобщает задачу, которой посвящена большая часть "Орграфы и DAG-графы" - поддержка быстрых запросов достижимости при ограничении на доступную память.

Первая рассматриваемая нами реализация функции АТД поиска кратчайших путей для всех пар вершин решает эту задачу, используя алгоритм Дейкстры для решения задачи с одним истоком для каждой вершины. C++ позволяет записать этот метод непосредственно (см. программу 21.4): для решения задачи с одним истоком для каждой вершины создается вектор объектов SPT. Этот метод обобщает метод на основе BFS для невзвешенных неориентированных графов, который был рассмотрен в "Виды графов и их свойства" . Он также похож на использование DFS в программе 19.4, где вычисляется транзитивное замыкание невзвешенного орграфа с началом в каждой вершине.

Программа 21.3. Вычисление взвешенного диаметра сети

Эта клиентская функция демонстрирует использование интерфейса из программы 21.2. Она находит самый длинный из кратчайших путей в данной сети, выводит путь и возвращает его вес (т.е. диаметр сети).

  template <class Graph, class Edge>
  double diameter(Graph &G)
    { int vmax = 0, wmax = 0;
      allSP<Graph, Edge> all(G);
      for (int v = 0; v < G.V(); v++)
        for (int w = 0; w < G.V(); w++)
          if (all.path(v, w))
            if (all.dist(v, w) > all.dist(vmax, wmax))
              { vmax = v; wmax = w; }
      int v = vmax; cout << v;
      while (v != wmax)
        { v = all.path(v, wmax)->w(); cout <<    << v; }
      return all.dist(vmax, wmax);
    }
      

Как и в задачах о кратчайших путях из одного истока и задачах вычисления MST, эта граница слишком осторожна; для типичных графов время выполнения обычно равно VE.

Для сравнений этой реализации с другими полезно рассмотреть матрицы, неявно образованные структурой вектора векторов приватных членов данных. Векторы wt образуют как раз матрицу расстояний, рассмотренную в разделе 21.1: элемент этой матрицы на пересечении строки s и столбца t содержит длину кратчайшего пути из s в t. Как показано на рис. 21.8 и 21.9, векторы spt образуют транспонированную матрицу путей: элемент на пересечении строки s и столбца t указывает на последнее ребро в кратчайшем пути из s в t.

Для насыщенных графов можно было бы использовать представление матрицей смежности и избежать вычисления обратного графа с помощью неявного транспонирования матрицы (поменяв местами индексы строк и столбцов), как в программе 19.7. Разработка такой реализации представляет собой интересное упражнение по программированию и приводит к компактной реализации (см. упражнение 21.43); однако другой подход, который будет рассмотрен ниже, допускает еще более компактную реализацию.

Рекомендуемый метод решения задачи поиска кратчайших путей для всех пар вершин в насыщенных графах был разработан Р. Флойдом (R. Floyd). Он точности повторяет метод Уоршалла, только вместо использования логической операции ИЛИ для отслеживания существования путей он проверяет расстояния для каждого ребра, чтобы определить, является ли это ребро частью нового, более короткого пути.

Программа 21.4. Алгоритм Дейкстры для поиска всех кратчайших путей

Этот класс использует алгоритм Дейкстры, чтобы построить SPT для каждой вершины. Это позволяет выполнять функции pathR и dist для любой пары вершин.

  #include "SPT.cc"
  template <class Graph, class Edge>
  class allSP
    { const Graph &G;
      vector< SPT<Graph, Edge> *> A;
    public:
      allSP(const Graph &G) : G(G), A(G.V())
        { for (int s = 0; s < G.V(); s++)
          A[s] = new SPT<Graph, Edge>(G, s);
        }
      Edge *pathR(int s, int t) const
        { return A[s]->pathR(t); }
      double dist(int s, int t) const
        { return A[s]->dist(t); }
    };
      

Как уже было сказано, в соответствующей абстрактной постановке алгоритмы Флойда и Уоршалла идентичны (см. "Орграфы и DAG-графы" и 21.1).

Программа 21.5 содержит функцию АТД поиска кратчайших путей для всех пар вершин, которая реализует алгоритм Флойда. В ней явно используются матрицы из раздела 21.1 как приватные члены данных: вектор векторов d размером V х V для матрицы расстояний и еще один вектор векторов p размером V х V для таблицы путей. Для каждой пары вершин s и t конструктор заносит в d[s][t] длину кратчайшего пути из s в t (которая возвращается функцией-членом dist), а в p[s][t] - индекс следующей вершины на кратчайшем пути из s в t (который возвращается функцией-членом path). Реализация основана на операции релаксации пути, рассмотренной в разделе 21.1.

Программа 21.5. Алгоритм Флойда для поиска всех кратчайших путей

Эта реализация интерфейса из программы 21.2 использует алгоритм Флойда - обобщение алгоритма Уоршалла (см. программу 19.3), которое находит кратчайшие пути между каждой парой точек, а не просто проверяет их существование.

После первоначального занесения ребер графа в матрицы расстояний и путей выполняется последовательность операций релаксации для вычисления кратчайших путей. Алгоритм прост для реализации, хотя проверка того, что он вычисляет кратчайшие пути, более сложна (см. текст).

  template <class Graph, class Edge>
  class allSP
    { const Graph &G;
      vector <vector <Edge *> > p;
      vector <vector <double> > d;
    public:
      allSP(const Graph &G) : G(G), p(G.V()), d(G.V())
        { int V = G.V();
          for (int i = 0; i < V; i++)
            { p[i].assign(V, 0); d[i].assign(V, V); }
          for (int s = 0; s < V; s++)
            for (int t = 0; t < V; t++)
              if (G.edge(s, t))
                { p[s][t] = G.edge(s, t);
                  d[s][t] = G.edge(s, t)->wt();
                }
          for (int s = 0; s < V; s++) d[s][s] = 0;
          for (int i = 0; i < V; i++)
            for (int s = 0; s < V; s++) if (p[s][i])
              for (int t = 0; t < V; t++) if (s != t)
                if (d[s][t] > d[s][i] + d[i][t])
                  { p[s][t] = p[s][i];
                    d[s][t] = d[s][i] + d[i][t];
                  }
        }
      Edge *path(int s, int t) const
        { return p[s][t]; }
      double dist(int s, int t) const
        { return d[s][t]; }
    };
      

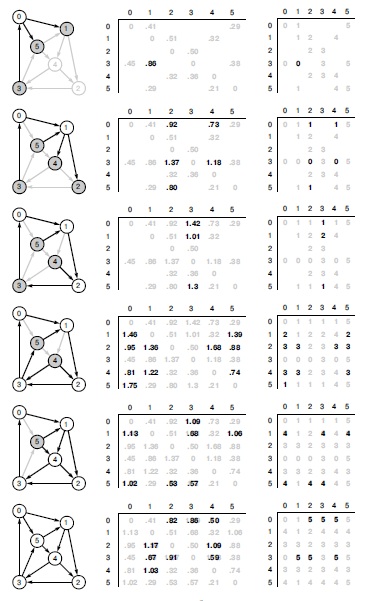
На рис. 21.14 показана подробная трасса выполнения алгоритма Флойда для нашей демонстрационной сети. Если преобразовать каждый пустой элемент в 0 (указание на отсутствие ребра), а каждый непустой элемент - в 1 (указание на наличие ребра), то эти матрицы описывают работу алгоритма Уоршалла точно так же, как на рис. 19.15. В случае алгоритма Флойда непустые элементы не только указывают существование пути, но и дают информацию об известном кратчайшем пути. Элемент в матрице расстояний содержит длину известного кратчайшего пути, который соединяет вершины, соответствующие данной строке и столбцу; соответствующий элемент в матрице путей дает следующую вершину на этом пути. По мере заполнения матриц непустыми элементами алгоритм Уоршалла просто перепроверяет, соединяют ли новые пути пары вершин, которые уже соединены известными путями. В отличие от этого, алгоритм Флойда должен проверить (и при необходимости обновить) каждый новый путь, чтобы убедиться, что он приводит к более коротким путям.

Сравнивая оценки времени выполнения в худшем случае для алгоритмов Дейкстры и Флойда, можно получить тот же результат для алгоритмов поиска кратчайших путей для всех пар вершин, что и для соответствующих алгоритмов транзитивного замыкания в "Орграфы и DAG-графы" . Понятно, что для разреженных сетей более подходит выполнение алгоритма Дейкстры из каждой вершины, поскольку время работы близко к VE. По мере возрастания насыщенности графа с ним все более конкурирует алгоритм Флойда, который всегда требует времени, пропорционального V³ (см. упражнение 21.67); он широко используется ввиду простоты реализации.

Более существенное различие между этими алгоритмами, которое подробно рассматривается в разделе 21.7, состоит в том, что алгоритм Флойда эффективен даже на сетях, где возможны отрицательные веса (при условии, что нет отрицательных циклов). Как было сказано в разделе 21.2, метод Дейкстры в таких графах не обязательно находит кратчайшие пути.

Классические решения описанной задачи поиска кратчайших путей для всех пар вершин предполагают, что имеется объем памяти, достаточный для хранения матриц расстояний и путей. Огромные разреженные графы, матрицы V х V которых слишком велики для хранения в памяти, представляют еще одну интересную и перспективную область. Как было показано в "Орграфы и DAG-графы" , до сих пор является открытой задача сведения затрат памяти до величины, пропорциональной V, при сохранении поддержки линейного времени ответов на запросы длины кратчайших путей.

Рис. 21.14. Алгоритм Флойда

Эта последовательность показывает построение матриц кратчайших путей для всех пар вершин с помощью алгоритма Флойда. Для i от 0 до 5 (сверху вниз), мы рассматриваем для всех s и t все пути из s в t, в которых нет промежуточных вершин, больших i (заштрихованные вершины). Вначале единственными такими путями являются ребра сети, поэтому матрица расстояний (в центре) представляет собой матрицу смежности графа, а в матрицу путей (справа) для каждогоребра s-t заносится p[s][t]= t. Для вершины 0 (вверху) алгоритм находит, что путь 3-0-1 короче сигнального значения, которое означает отсутствие ребра 3-1, и соответствующим образом обновляет матрицы. Это не делается для путей наподобие 3-0-5, который не короче известного пути 3-5. Далее алгоритм рассматривает пути, проходящие через 0 и 1 (второй ряд сверху) и находит новые более короткие пути 0-1-2, 0-1-4, 3-0-1-2, 3-0-1-4 и 5-1-2. В третьем ряду сверху показаны обновления, соответствующие более коротким путям через 0, 1, 2 и т.д.

Черные числа, записанные поверх серых в матрицах, указывают на ситуации, где алгоритм находит более короткий путь, чем найденный раньше. Например, в строке 3 и столбце 2 в нижнем ряду поверх 1.37 записано 0.91, поскольку алгоритм обнаружил, что путь 3-5-4-2 короче пути 3-0-1-2.

Мы выяснили, что имеется аналогичная трудноразрешимая проблема даже для более простой задачи достижимости (где достаточно было за линейное время узнать, имеется ли вообще какой-либо путь, соединяющий данную пару вершин), поэтому нельзя ожидать простого решения задачи поиска кратчайших путей для всех пар вершин. Вообще-то количество различных кратчайших длин путей в общем случае пропорционально V² даже для разреженных графов. Эта величина в некотором смысле служит мерой объема информации, которую требуется обработать, и, возможно, указывает, что если существует ограничение на объем памяти, то следует ожидать большего времени обработки каждого запроса (см. упражнения 21.48-21.50).

Упражнения

21.39. Оцените с точностью до порядка наибольший размер (количество вершин) графа, который ваш компьютер и система программирования могут обработать за 10 секунд, если для вычисления кратчайших путей использовать алгоритм Флойда.

21.40. Оцените с точностью до порядка наибольший размер (количество ребер) графа с насыщенностью 10, который ваш компьютер и система программирования могут обработать за 10 секунд, если для вычисления кратчайших путей использовать алгоритм Дейкстры.

21.41. Покажите в стиле рис. 21.9 результат применения алгоритма Дейкстры для вычисления всех кратчайших путей в сети, определенной в упражнении 21.1.

21.42. Покажите в стиле рис. 21.14 результат применения алгоритма Флойда для вычисления всех кратчайших путей в сети, определенной в упражнении 21.1.

21.43. Объедините программу 20.6 с программой 21.4 для реализации интерфейса АТД поиска кратчайших путей для всех пар вершин (на основе алгоритма Дейкстры) в насыщенных сетях, который поддерживает вызовы функции path, но не вычисляет явно обратную сеть. Не определяйте отдельную функцию для решения задачи с одним истоком - поместите код из программы 20.6 непосредственно во внутренний цикл и храните результаты непосредственно в приватных членах данных d и p, как в программе 21.5.

21.44. Эмпирически сравните в стиле таблицы 20.2 алгоритм Дейкстры (программа 21.4 и упражнение 21.43) и алгоритм Флойда (программа 21.5) для различных сетей (см. упражнения 21.4-21.8).

21.45. Эмпирически определите, сколько раз алгоритмы Флойда и Дейкстры обновляют значения в матрице расстояний для различных сетей (см. упражнения 21.4-21.8).

21.46. Приведите матрицу, в которой элемент в строке s и столбце t равен количеству различных простых направленных путей, соединяющих s и t на рис. 21.1.

21.47. Реализуйте класс, конструктор которого вычисляет матрицу количества путей, описанную в упражнении 21.46, чтобы общедоступная функция-член могла выдавать это количество за постоянное время.

21.48. Разработайте реализацию класса для абстрактного АТД поиска кратчайших путей для разреженных графов, в которой необходимый объем памяти сокращается до величин, пропорциональных V, а время запроса увеличивается до значений, пропорциональных V.

21.49. Разработайте реализацию абстрактного класса АТД поиска кратчайших путей для разреженных графов, которая использует объем памяти, существенно меньший O(V²), но поддерживает запросы за время, намного меньшее O(V). Указание. Вычислите все кратчайшие пути для подмножества вершин.

21.50. Разработайте реализацию абстрактного класса АТД поиска кратчайших путей для разреженных графов, которая использует объем памяти, существенно меньший O( V²), и поддерживает (с помощью рандомизации) запросы за линейное ожидаемое время.

21.51. Разработайте реализацию абстрактного класса АТД поиска кратчайших путей, в которой используется ленивый подход применения алгоритма Дейкстры: SPT-дерево (и связанный с ним вектор расстояний) для вершины s строится при первом запросе клиентом кратчайшего пути из s, а при последующих запросах выбирается готовая информация.

21.52. Измените АТД кратчайших путей и алгоритм Дейкстры, чтобы вычислять кратчайшие путей в сетях, в которых веса имеют и вершины, и ребра. Не переделывайте представление графа (метод описан в упражнении 21.4), а измените код.

21.53. Постройте небольшую модель авиамаршрутов и времен перелета - возможно, на основе ваших путешествий. Воспользуйтесь решением упражнения 21.52 для вычисления наиболее быстрого пути от одного из пунктов к другому. Затем протестируйте полученную программу на реальных данных (см. упражнение 21.5).