Параллельные методы умножения матрицы на вектор

6.8. Краткий обзор лекции

В данной лекции на примере задачи умножения матрицы на вектор рассматриваются возможные схемы разделения матриц между процессорами многопроцессорной вычислительной системы, которые могут быть использованы для организации параллельных вычислений при выполнении матричных операций. В числе излагаемых схем способы разбиения матриц на полосы (по вертикали или горизонтали) или на прямоугольные наборы элементов ( блоки ).

Далее в лекции с использованием рассмотренных способов разделения матриц подробно излагаются три возможных варианта параллельного выполнения операции умножения матрицы на вектор. Первый алгоритм основан на разделении матрицы между процессорами по строкам, второй – на разделении матрицы по столбцам, а третий – на блочном разделении данных. Каждый алгоритм представлен в соответствии с общей схемой, описанной в "Принципы разработки параллельных методов" , — вначале определяются базовые подзадачи, затем выделяются информационные зависимости подзадач, далее обсуждается масштабирование и распределение подзадач между процессорами. В завершение для каждого алгоритма проводится анализ эффективности получаемых параллельных вычислений и приводятся результаты вычислительных экспериментов. Для алгоритма умножения матрицы на вектор при ленточном разделении данных по строкам приводится возможный вариант программной реализации.

Полученные показатели эффективности показывают, что все используемые способы разделения данных приводят к равномерной балансировке вычислительной нагрузки, и отличия имеются только в трудоемкости выполняемых информационных взаимодействий между процессорами. В этом отношении представляется интересным проследить, как выбор способа разделения данных влияет на характер необходимых операций передачи данных, и выделить основные различия в коммуникационных действиях разных алгоритмов. Кроме того, важным является определение целесообразной структуры линий связи между процессорами для эффективного выполнения соответствующего параллельного алгоритма. Так, например, алгоритмы, основанные на ленточном разделении данных, ориентированы на топологию сети в виде гиперкуба или полного графа. Для реализации алгоритма, основанного на блочном разделении данных, необходимо наличие топологии решетки.

На рис. 6.11 на общем графике представлены показатели ускорения, полученные в результате выполнения вычислительных экспериментов для всех рассмотренных алгоритмов. Следует отметить, что дополнительные расчеты показывают , что при большем количестве процессоров и при большом размере матриц более эффективным становится блочный алгоритм умножения.

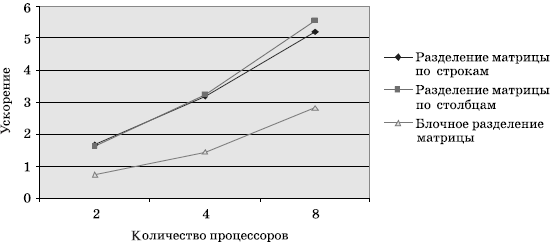
Рис. 6.11. Показатели ускорения рассмотренных параллельных алгоритмов умножения по результатам вычислительных экспериментов с матрицами размера 2000x2000 и векторами из 2000 элементов

6.9. Обзор литературы

Задача умножения матрицы на вектор часто используется как демонстрационный пример параллельного программирования и, как результат, широко рассматривается в литературе. В качестве дополнительного учебного материала могут быть рекомендованы работы [ [ 2 ] , [ 51 ] , [ 63 ] ]. Широкое обсуждение вопросов параллельного выполнения матричных вычислений выполнено в работе [ [ 30 ] ].

При рассмотрении вопросов программной реализации параллельных методов может быть рекомендована работа [ [ 23 ] ]. В ней рассматривается хорошо известная и широко применяемая в практике параллельных вычислений программная библиотека численных методов ScaLAPACK.

6.10. Контрольные вопросы

1. Назовите основные способы распределения элементов матрицы между процессорами вычислительной системы.
2. В чем состоит постановка задачи умножения матрицы на вектор?
3. Какова вычислительная сложность последовательного алгоритма умножения матрицы на вектор?
4. Почему при разработке параллельных алгоритмов умножения матрицы на вектор допустимо дублировать вектор-операнд на все процессоры?
5. Какие подходы могут быть предложены для разработки параллельных алгоритмов умножения матрицы на вектор?
6. Представьте общие схемы рассмотренных параллельных алгоритмов умножения матрицы на вектор.
7. Проведите анализ и получите показатели эффективности для одного из рассмотренных алгоритмов.
8. Какой из представленных алгоритмов умножения матрицы на вектор обладает лучшими показателями ускорения и эффективности?
9. Может ли использование циклической схемы разделения данных повлиять на время работы каждого из представленных алгоритмов?
10. Какие информационные взаимодействия выполняются для алгоритмов при ленточной схеме разделения данных? В чем различие необходимых операций передачи данных при разделении матрицы по строкам и столбцам?
11. Какие информационные взаимодействия выполняются для блочного алгоритма умножения матрицы на вектор?
12. Какая топология коммуникационной сети является целесообразной для каждого из рассмотренных алгоритмов?
13. Дайте общую характеристику программной реализации алгоритма умножения матрицы на вектор при разделении данных по строкам. В чем могут состоять различия в программной реализации других рассмотренных алгоритмов?
14. Какие функции библиотеки MPI оказались необходимыми при программной реализации алгоритмов?

6.11. Задачи и упражнения

1. Выполните реализацию параллельного алгоритма, основанного на ленточном разбиении матрицы на вертикальные полосы. Постройте ие оценки времени работы этого алгоритма с учетом параметров используемой вычислительной системы. Проведите вычислительные эксперименты. Сравните результаты реальных экспериментов с ранее подготовленными теоретическими оценками.
2. Выполните реализацию параллельного алгоритма, основанного на разбиении матрицы на блоки. Постройте теоретические оценки времени работы этого алгоритма с учетом параметров используемой вычислительной системы. Проведите вычислительные эксперименты. Сравните результаты реальных экспериментов с ранее подготовленными теоретическими оценками.