Параллельные методы умножения матрицы на вектор
6.6. Умножение матрицы на вектор при разделении данных по столбцам
Рассмотрим теперь другой подход к параллельному умножению матрицы на вектор, основанный на разделении исходной матрицы на непрерывные наборы (вертикальные полосы) столбцов.
6.6.1. Определение подзадач и выделение информационных зависимостей
При таком способе разделения данных в качестве базовой подзадачи может быть выбрана операция умножения столбца матрицы А на один из элементов вектора b. Для организации вычислений в этом случае каждая базовая подзадача i, 0<=i<n, должна содержать i -й столбец матрицы А и i -е элементы bi и ci векторов b и с.
Параллельный алгоритм умножения матрицы на вектор начинается с того, что каждая базовая задача i выполняет умножение своего столбца матрицы А на элемент bi, в итоге в каждой подзадаче получается вектор c'(i) промежуточных результатов. Далее для получения элементов результирующего вектора с подзадачи должны обменяться своими промежуточными данными между собой (элемент j, 0<=j<n, частичного результата c'(i) подзадачи i, 0<=i<n, должен быть передан подзадаче j ). Данная обобщенная передача данных ( all-to-all communication или total exchange ) является наиболее общей коммуникационной процедурой и может быть реализована при помощи функции MPI_Alltoall библиотеки MPI. После выполнения передачи данных каждая базовая подзадача i, 0<=i<n, будет содержать n частичных значений c'i(j), 0<=j<n, сложением которых и определяется элемент ci вектора результата с (см. рис. 6.5).
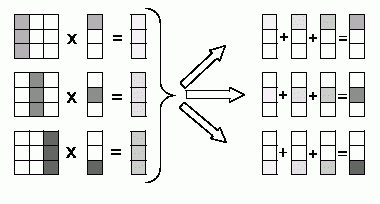
Рис. 6.5. Организация вычислений при выполнении параллельного алгоритма умножения матрицы на вектор с использованием разбиения матрицы по столбцам
6.6.2. Масштабирование и распределение подзадач по процессорам
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и равным объемом передаваемых данных. В случае когда количество столбцов матрицы превышает число процессоров, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних столбцов (в этом случае исходная матрица A разбивается на ряд вертикальных полос). При соблюдении равенства размера полос такой способ агрегации вычислений обеспечивает равномерность распределения вычислительной нагрузки по процессорам, составляющим многопроцессорную вычислительную систему.
Как и в предыдущем алгоритме, распределение подзадач между процессорами вычислительной системы может быть выполнено произвольным образом.
6.6.3. Анализ эффективности
Пусть, как и ранее, матрица А является квадратной, то есть m=n. На первом этапе вычислений каждый процессор умножает принадлежащие ему столбцы матрицы А на элементы вектора b, после умножения полученные значения суммируются для каждой строки матрицы А в отдельности
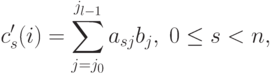 |
( 6.9) |
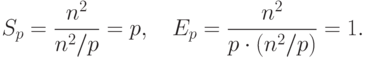 |
( 6.10) |
Теперь рассмотрим более точные соотношения для оценки времени выполнения параллельного алгоритма. С учетом ранее проведенных рассуждений время выполнения вычислительных операций алгоритма может быть оценено при помощи выражения
![T_p(cacl)=[n \cdot (2 \cdot \lceil n/p \rceil - 1) + n] \cdot \tau](/sites/default/files/tex_cache/41283c2c14d8fd2c5352b6f0884bb691.png) |
( 6.11) |
 есть время выполнения одной
элементарной скалярной операции).
есть время выполнения одной
элементарной скалярной операции).Для выполнения операции обобщенной передачи данных рассмотрим два возможных способа реализации (см. также "Оценка коммуникационной трудоемкости параллельных алгоритмов" ). Первый способ обеспечивается алгоритмом, согласно которому каждый процессор последовательно передает свои данные всем остальным процессорам вычислительном системы. Предположим, что процессоры могут одновременно отправлять и принимать сообщения и между любой парой процессоров имеется прямая линия связи, тогда оценка трудоемкости (время исполнения) такого алгоритма обобщенной передачи данных может быть определена как
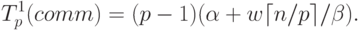 |
( 6.12) |
 – латентность сети передачи данных,
– латентность сети передачи данных,  – пропускная способность сети, w – размер элемента
данных в байтах).
– пропускная способность сети, w – размер элемента
данных в байтах).Второй способ выполнения операции обмена данными рассмотрен в
"Оценка коммуникационной трудоемкости параллельных алгоритмов"
, когда топология
вычислительной сети может быть представлена в виде гиперкуба. Как
было показано, выполнение такого алгоритма может быть
осуществлено за  шагов, на каждом из которых каждый процессор передает и получает
сообщение из n/2 элементов. Как результат, время операции передачи данных при таком подходе составляет величину:
шагов, на каждом из которых каждый процессор передает и получает
сообщение из n/2 элементов. Как результат, время операции передачи данных при таком подходе составляет величину:
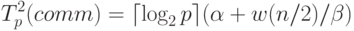 |
( 6.13) |
С учетом (6.11) – (6.13) общее время выполнения параллельного алгоритма умножения матрицы на вектор при разбиении данных по столбцам выражается следующими соотношениями.
- Для первого способа выполнения операции передачи данных
![T_p^1=[n\cdot(2\cdot\lceil n/p\rceil -1)+n]\cdot\tau+(p-1)(\alpha+w\lceil n/p \rceil / \beta).](/sites/default/files/tex_cache/b530fac9345a247b962a845bbab70f76.png)
( 6.14) - Для второго способа выполнения операции передачи данных
![T_p^2=[n\cdot(2\cdot\lceil n/p\rceil -1)+n]\cdot\tau+ \lceil \log_2 p \rceil (\alpha+w(n/2) / \beta).](/sites/default/files/tex_cache/9f349329ded3e7fdb07ae6f3eb5ff19c.png)
( 6.15)
6.6.4. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного алгоритма умножения матрицы на вектор при разбиении данных по столбцам проводились при условиях, указанных в п. 6.5.5. Результаты вычислительных экспериментов приведены в таблице 6.3.
| Размер матрицы | Последовательный алгоритм | Параллельный алгоритм | |||||
|---|---|---|---|---|---|---|---|
| 2 процессора | 4 процессора | 8 процессоров | |||||
| Время | Ускорение | Время | Ускорение | Время | Ускорение | ||
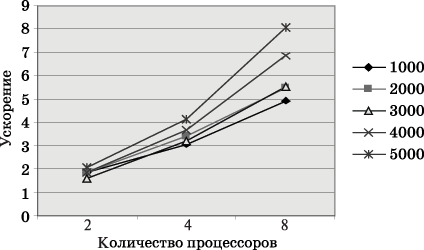
| 1000 | 0,0041 | 0,0022 | 1,8352 | 0,0015 | 3,1538 | 0,0008 | 4,9409 |
| 2000 | 0,016 | 0,0085 | 1,8799 | 0,0046 | 3,4246 | 0,0029 | 5,4682 |
| 3000 | 0,031 | 0,019 | 1,6315 | 0,0095 | 3,2413 | 0,0055 | 5,5456 |
| 4000 | 0,062 | 0,0331 | 1,8679 | 0,0168 | 3,6714 | 0,0090 | 6,8599 |
| 5000 | 0,11 | 0,0518 | 2,1228 | 0,0265 | 4,1361 | 0,0136 | 8,0580 |
Сравнение экспериментального времени 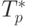 выполнения эксперимента и времени Tp,
вычисленного по соотношениям (6.14), (6.15), представлено в
таблице 6.4 и на рис.
6.6 и
6.7. Теоретическое время
выполнения эксперимента и времени Tp,
вычисленного по соотношениям (6.14), (6.15), представлено в
таблице 6.4 и на рис.
6.6 и
6.7. Теоретическое время 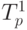 вычисляется согласно (6.14), а теоретическое
время
вычисляется согласно (6.14), а теоретическое
время 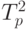 – в соответствии с (6.15).
– в соответствии с (6.15).
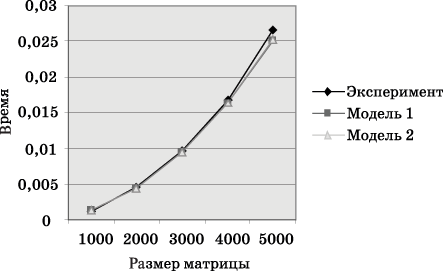
Рис. 6.6. График зависимости теоретического и экспериментального времени выполнения параллельного алгоритма на четырех процессорах от объема исходных данных (ленточное разбиение матрицы по столбцам)
| Размер матрицы | 2 процессора | 4 процессора | 8 процессоров | ||||||
|---|---|---|---|---|---|---|---|---|---|
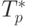 |
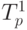 |
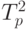 |
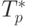 |
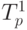 |
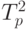 |
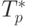 |
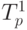 |
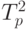 |
|
| 1000 | 0,0022 | 0,0021 | 0,0021 | 0,0013 | 0,0013 | 0,0014 | 0,0008 | 0,0011 | 0,0015 |
| 2000 | 0,0085 | 0,0082 | 0,0080 | 0,0046 | 0,0044 | 0,0044 | 0,0029 | 0,0027 | 0,0031 |
| 3000 | 0,019 | 0,0177 | 0,0177 | 0,0095 | 0,0094 | 0,0094 | 0,0055 | 0,0054 | 0,0056 |
| 4000 | 0,0331 | 0,0313 | 0,0313 | 0,0168 | 0,0163 | 0,0162 | 0,0090 | 0,0090 | 0,0091 |
| 5000 | 0,0518 | 0,0487 | 0,0487 | 0,0265 | 0,0251 | 0,0251 | 0,0136 | 0,0135 | 0,0136 |