НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 6: Параллельные методы умножения матрицы на вектор

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Доступ: свободный | Студентов: 2035 / 507 | Оценка: 4.53 / 4.26 | Длительность: 25:10:00

ISBN: 978-5-9556-0096-3

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.2. Постановка задачи

В результате умножения матрицы А размерности m x n и вектора b, состоящего из n элементов, получается вектор c размера m, каждый i -й элемент которого есть результат скалярного умножения i -й строки матрицы А (обозначим эту строчку a_i ) и вектора b:

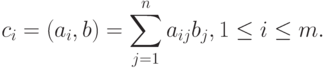$c_i = (a_i, b) = \sum_{j=1}^n a_{ij}b_j, 1 \le i \le m.$

( 6.4)

Тем самым получение результирующего вектора c предполагает повторение m однотипных операций по умножению строк матрицы A и вектора b. Каждая такая операция включает умножение элементов строки матрицы и вектора b ( n операций) и последующее суммирование полученных произведений ( n-1 операций). Общее количество необходимых скалярных операций есть величина

T₁=mx(2n-1)

6.3. Последовательный алгоритм

Последовательный алгоритм умножения матрицы на вектор может быть представлен следующим образом.

Алгоритм 6.1. Последовательный алгоритм умножения матрицы на вектор

// Алгоритм 6.1
// Поcледовательный алгоритм умножения матрицы на вектор
for (i = 0; i < m; i++){
  c[i] = 0;
  for (j = 0; j < n; j++){
    c[i] += A[i][j]*b[j]
  }
}

Матрично-векторное умножение – это последовательность вычисления скалярных произведений. Поскольку каждое вычисление скалярного произведения векторов длины n требует выполнения n операций умножения и n-1 операций сложения, его трудоемкость порядка O(n). Для выполнения матрично-векторного умножения необходимо осуществить m операций вычисления скалярного произведения, таким образом, алгоритм имеет трудоемкость порядка O(mn).

6.4. Разделение данных

При выполнении параллельных алгоритмов умножения матрицы на вектор, кроме матрицы А, необходимо разделить еще вектор b и вектор результата c. Элементы векторов можно продублировать, то есть скопировать все элементы вектора на все процессоры, составляющие многопроцессорную вычислительную систему, или разделить между процессорами. При блочном разбиении вектора из n элементов каждый процессор обрабатывает непрерывную последовательность из k элементов вектора (мы предполагаем, что размерность вектора n нацело делится на число процессоров, т.е. n= kxp ).

Поясним, почему дублирование векторов b и c между процессорами является допустимым решением (далее для простоты изложения будем полагать, что m=n ). Векторы b и с состоят из n элементов, т.е. содержат столько же данных, сколько и одна строка или один столбец матрицы. Если процессор хранит строку или столбец матрицы и одиночные элементы векторов b и с, то общее число сохраняемых элементов имеет порядок O(n). Если процессор хранит строку (столбец) матрицы и все элементы векторов b и с, то общее число сохраняемых элементов также порядка O(n). Таким образом, при дублировании и при разделении векторов требования к объему памяти из одного класса сложности.

6.5. Умножение матрицы на вектор при разделении данных по строкам

Рассмотрим в качестве первого примера организации параллельных матричных вычислений алгоритм умножения матрицы на вектор, основанный на представлении матрицы непрерывными наборами (горизонтальными полосами) строк. При таком способе разделения данных в качестве базовой подзадачи может быть выбрана операция скалярного умножения одной строки матрицы на вектор.

6.5.1. Выделение информационных зависимостей

Для выполнения базовой подзадачи скалярного произведения процессор должен содержать соответствующую строку матрицы А и копию вектора b. После завершения вычислений каждая базовая подзадача определяет один из элементов вектора результата c.

Для объединения результатов расчета и получения полного вектора c на каждом из процессоров вычислительной системы необходимо выполнить операцию обобщенного сбора данных (см. "Принципы разработки параллельных методов" ), в которой каждый процессор передает свой вычисленный элемент вектора c всем остальным процессорам. Этот шаг можно выполнить, например, с использованием функции MPI_Allgather из библиотеки MPI.

В общем виде схема информационного взаимодействия подзадач в ходе выполняемых вычислений показана на рис. 6.2.

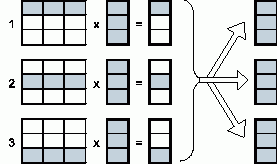
Организация вычислений при выполнении параллельного алгоритма умножения матрицы на вектор, основанного на разделении матрицы по строкам

Рис. 6.2. Организация вычислений при выполнении параллельного алгоритма умножения матрицы на вектор, основанного на разделении матрицы по строкам

6.5.2. Масштабирование и распределение подзадач по процессорам

В процессе умножения плотной матрицы на вектор количество вычислительных операций для получения скалярного произведения одинаково для всех базовых подзадач. Поэтому в случае когда число процессоров p меньше числа базовых подзадач m, мы можем объединить базовые подзадачи таким образом, чтобы каждый процессор выполнял несколько таких задач, соответствующих непрерывной последовательности строк матрицы А. В этом случае по окончании вычислений каждая базовая подзадача определяет набор элементов результирующего вектора с.

Распределение подзадач между процессорами вычислительной системы может быть выполнено произвольным образом.

6.5.3. Анализ эффективности

Для анализа эффективности параллельных вычислений здесь и далее будут строиться два типа оценок. В первой из них трудоемкость алгоритмов оценивается в количестве вычислительных операций, необходимых для решения поставленной задачи, без учета затрат времени на передачу данных между процессорами, а длительность всех вычислительных операций считается одинаковой. Кроме того, константы в получаемых соотношениях, как правило, не указываются — для первого типа оценок важен прежде всего порядок сложности алгоритма, а не точное выражение времени выполнения вычислений. Как результат, в большинстве случаев подобные оценки получаются достаточно простыми и могут быть использованы для начального анализа эффективности разрабатываемых алгоритмов и методов.

Второй тип оценок направлен на формирование как можно более точных соотношений для предсказания времени выполнения алгоритмов. Получение таких оценок проводится, как правило, при помощи уточнения выражений, полученных на первом этапе. Для этого в имеющиеся соотношения вводятся параметры, задающие длительность выполнения операций, строятся оценки трудоемкости коммуникационных операций, указываются все необходимые константы. Точность получаемых выражений проверяется при помощи вычислительных экспериментов, по результатам которых время выполненных расчетов сравнивается с теоретически предсказанными оценками длительностей вычислений. Как результат, оценки подобного типа имеют, как правило, более сложный вид, но позволяют более точно оценивать эффективность разрабатываемых методов параллельных вычислений.

Рассмотрим трудоемкость алгоритма умножения матрицы на вектор. В случае если матрица А квадратная ( m=n ), последовательный алгоритм умножения матрицы на вектор имеет сложность T₁=n². В случае параллельных вычислений каждый процессор производит умножение только части (полосы) матрицы A на вектор b, размер этих полос равен n/p строк. При вычислении скалярного произведения одной строки матрицы и вектора необходимо произвести n операций умножения и (n-1) операций сложения. Следовательно, вычислительная трудоемкость параллельного алгоритма определяется выражением:

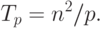( 6.5)

С учетом этой оценки показатели ускорения и эффективности параллельного алгоритма имеют вид:

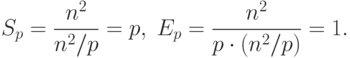$S_p = \frac{n^2}{n^2/p}=p, \; E_p = \frac{n^2}{p \cdot (n^2/p)} = 1.$

( 6.6)

Построенные выше оценки времени вычислений выражены в количестве операций и, кроме того, определены без учета затрат на выполнение операций передачи данных. Используем ранее высказанные предположения о том, что выполняемые операции умножения и сложения имеют одинаковую длительность $\tau$ . Кроме того, будем предполагать также, что вычислительная система является однородной, т.е. все процессоры, составляющие эту систему, обладают одинаковой производительностью. С учетом введенных предположений время выполнения параллельного алгоритма, связанное непосредственно с вычислениями, составляет

$T_p(calc)=\lceil n/p \rceil \cdot(2n-1)\cdot \tau$

(здесь и далее операция 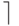$\lcei\ \rceil$ есть округление до целого в большую сторону).

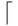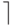Оценка трудоемкости операции обобщенного сбора данных уже выполнялась в "Принципы разработки параллельных методов" (см. п. 4.3.4). Как уже отмечалась ранее, данная операция может быть выполнена за $\lceil$ log₂p $\rceil$ итераций^{1Будем предполагать, что
топология вычислительной системы допускает возможность такого
эффективного способа выполнения операции обобщенного сбора данных
(это возможно, в частности, если структура сети передачи данных
имеет вид гиперкуба или полного графа).}. На первой итерации взаимодействующие пары процессоров обмениваются сообщениями объемом $w \lceil n/p\rceil$ ( w есть размер одного элемента вектора c в байтах), на второй итерации этот объем увеличивается вдвое и оказывается равным 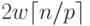$2w\lceil n/p \rceil$ и т.д. Как результат, длительность выполнения операции сбора данных при использовании модели Хокни может быть определена при помощи следующего выражения

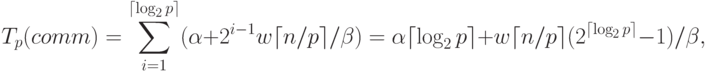$T_p(comm) = \sum_{i=1}^{\lceil \log_2 p \rceil} (\alpha + 2^{i-1}w\lceil n/p \rceil / \beta) = \alpha \lceil \log_2 p \rceil + w \lceil n/p \rceil (2^{\lceil \log_2 p \rceil} - 1)/\beta,$

( 6.7)

где $\alpha$ – латентность сети передачи данных, $\beta$ – пропускная способность сети. Таким образом, общее время выполнения параллельного алгоритма составляет

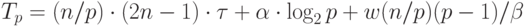$T_p=(n/p)\cdot (2n-1) \cdot \tau + \alpha \cdot \log_2 p +w(n/p)(p-1)/ \beta$

( 6.8)

(для упрощения выражения в (6.8) предполагалось, что значения n/p и log₂p являются целыми).

Дальше >>

Авторизоваться

Теория и практика параллельных вычислений

Параллельные методы умножения матрицы на вектор