Параллельные методы умножения матрицы на вектор
6.7. Умножение матрицы на вектор при блочном разделении данных
Рассмотрим теперь параллельный алгоритм умножения матрицы на вектор, который основан на ином способе разделения данных – на разбиении матрицы на прямоугольные фрагменты ( блоки ).
6.7.1. Определение подзадач
Блочная схема разбиения матриц подробно рассмотрена в подразделе 6.1. При таком способе разделения данных исходная матрица A представляется в виде набора прямоугольных блоков:

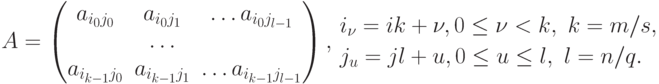
При использовании блочного представления матрицы A базовые подзадачи целесообразно определить на основе вычислений, выполняемых над матричными блоками. Для нумерации подзадач могут применяться индексы располагаемых в подзадачах блоков матрицы A, т.е. подзадача (i,j) содержит блок Aij. Помимо блока матрицы A каждая подзадача должна содержать также и блок вектора b. При этом для блоков одной и той же подзадачи должны соблюдаться определенные правила соответствия – операция умножения блока матрицы A ij может быть выполнена только, если блок вектора b'(i,j) имеет вид

6.7.2. Выделение информационных зависимостей
Рассмотрим общую схему параллельных вычислений для операции умножения матрицы на вектор при блочном разделении исходных данных. После перемножения блоков матрицы A и вектора b каждая подзадача (i,j) будет содержать вектор частичных результатов c'(i,j), определяемый в соответствии с выражениями

Поэлементное суммирование векторов частичных результатов для каждой горизонтальной полосы (данная процедура часто именуется операцией редукции – см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" ) блоков матрицы A позволяет получить результирующий вектор c
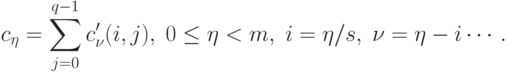
Для размещения вектора c применим ту же схему, что и для исходного вектора b: организуем вычисления таким образом, чтобы при завершении расчетов вектор c располагался поблочно в каждой из вертикальных полос блоков матрицы A (тем самым, каждый блок вектора c должен быть продублирован по каждой горизонтальной полосе). Выполнение всех необходимых действий для этого – суммирование частичных результатов и дублирование блоков результирующего вектора — может быть обеспечено при помощи функции MPI_Allreduce библиотеки MPI.
Общая схема выполняемых вычислений для умножения матрицы на вектор при блочном разделении данных показана на рис. 6.8.
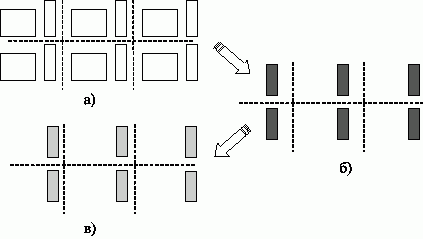
Рис. 6.8. Общая схема параллельного алгоритма умножения матрицы на вектор при блочном разделении данных: a) исходное распределение результатов, б) распределение векторов частичных результатов, в) распределение блоков результирующего вектора c
Рассмотрев представленную схему параллельных вычислений, можно сделать вывод, что информационная зависимость базовых подзадач проявляется только на этапе суммирования результатов перемножения блоков матрицы A и блоков вектора b. Выполнение таких расчетов может быть выполнено по обычной каскадной схеме (см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" ), и, как результат, характер имеющихся информационных связей для подзадач одной и той же горизонтальной полосы блоков соответствует структуре двоичного дерева.
6.7.3. Масштабирование и распределение подзадач по процессорам
Размер блоков матрицы А может быть подобран таким образом, чтобы общее количество базовых подзадач совпадало с числом процессоров p. Так, например, если определить размер блочной решетки как p=sxq, то
k=m/s, l=n/q,
где k и l есть количество строк и столбцов в блоках матрицы А. Такой способ определения размера блоков приводит к тому, что объем вычислений в каждой подзадаче является равным, и, тем самым, достигается полная балансировка вычислительной нагрузки между процессорами.
Возможность выбора остается при определении размеров блочной структуры матрицы А. Большое количество блоков по горизонтали приводит к возрастанию числа итераций в операции редукции результатов блочного умножения, а увеличение размера блочной решетки по вертикали повышает объем передаваемых данных между процессорами. Простое, часто применяемое решение состоит в использовании одинакового количества блоков по вертикали и горизонтали, т.е.
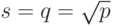
Следует отметить, что блочная схема разделения данных является обобщением всех рассмотренных в данной лекции подходов. Действительно, при q=1 блоки сводятся к горизонтальным полосам матрицы А, при s=1 исходные данные разбиваются на вертикальные полосы.
При решении вопроса распределения подзадач между процессорами должна учитываться возможность эффективного выполнения операции редукции. Возможный вариант подходящего способа распределения состоит в выделении для подзадач одной и той же горизонтальной полосы блоков множества процессоров, структура сети передачи данных между которыми имеет вид гиперкуба или полного графа.
6.7.4. Анализ эффективности
Выполним анализ эффективности параллельного алгоритма умножения матрицы на вектор при обычных уже предположениях, что матрица А является квадратной, т.е. m=n. Будем предполагать также, что процессоры, составляющие многопроцессорную вычислительную систему, образуют прямоугольную решетку p=sxq ( s – количество строк в процессорной решетке, q – количество столбцов).
Общий анализ эффективности приводит к идеальным показателям параллельного алгоритма:
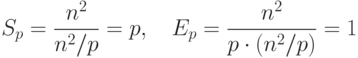 |
( 6.16) |
Для уточнения полученных соотношений оценим более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
Общее время умножения блоков матрицы А и вектора b может быть определено как
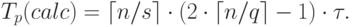 |
( 6.17) |
Операция редукции данных может быть выполнена с использованием
каскадной схемы и включает, тем самым, log2q итераций передачи сообщений размера 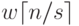 . Как результат, оценка
коммуникационных затрат параллельного алгоритма при использовании
модели Хокни может быть определена при помощи следующего
выражения
. Как результат, оценка
коммуникационных затрат параллельного алгоритма при использовании
модели Хокни может быть определена при помощи следующего
выражения
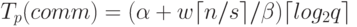 |
( 6.18) |
Таким образом, общее время выполнения параллельного алгоритма умножения матрицы на вектор при блочном разделении данных составляет
 |
( 6.19) |
6.7.5. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного алгоритма проводились при тех же условиях, что и ранее выполненные расчеты (см. п. 6.5.5). Результаты экспериментов приведены в таблице 6.5. Вычисления проводились с использованием четырех и девяти процессоров.
Сравнение экспериментального времени 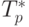 выполнения эксперимента и теоретического времени T
p, вычисленного в соответствии с выражением (6.19),
представлено в таблице 6.5 и на
рис. 6.10.
выполнения эксперимента и теоретического времени T
p, вычисленного в соответствии с выражением (6.19),
представлено в таблице 6.5 и на
рис. 6.10.
| Размер матриц | Последовательный алгоритм | Параллельный алгоритм | |||
|---|---|---|---|---|---|
| 4 процессора | 9 процессоров | ||||
| Время | Ускорение | Время | Ускорение | ||
| 1000 | 0,0041 | 0,0028 | 1,4260 | 0,0011 | 3,7998 |
| 2000 | 0,016 | 0,0099 | 1,6127 | 0,0095 | 3,2614 |
| 3000 | 0,031 | 0,0214 | 1,4441 | 0,0095 | 3,2614 |
| 4000 | 0,062 | 0,0381 | 1,6254 | 0,0175 | 3,5420 |
| 5000 | 0,11 | 0,0583 | 1,8860 | 0,0263 | 4,1755 |

Рис. 6.9. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма умножения матрицы на вектор (блочное разбиение матрицы) для разных размеров матриц
| Размер матриц | Последовательный алгоритм | Параллельный алгоритм | ||
|---|---|---|---|---|
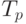 |
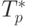 |
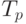 |
 |
|
| 1000 | 0,0025 | 0,0028 | 0,0012 | 0,0011 |
| 2000 | 0,0095 | 0,0099 | 0,0043 | 0,0042 |
| 3000 | 0,0212 | 0,0214 | 0,0095 | 0,0095 |
| 4000 | 0,0376 | 0,0381 | 0,0168 | 0,0175 |
| 5000 | 0,0586 | 0,0583 | 0,0262 | 0,0263 |

