Параллельные методы матричного умножения

7.1. Постановка задачи

Умножение матрицы A размера mxn и матрицы B размера nxl приводит к получению матрицы С размера mxl, каждый элемент которой определяется в соответствии с выражением:

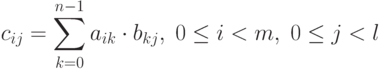( 7.1)

Как следует из (7.1), каждый элемент результирующей матрицы С есть скалярное произведение соответствующих строки матрицы A и столбца матрицы B:

( 7.2)

Этот алгоритм предполагает выполнение mxnxl операций умножения и столько же операций сложения элементов исходных матриц. При умножении квадратных матриц размера nxn количество выполненных операций имеет порядок O(n³). Известны последовательные алгоритмы умножения матриц, обладающие меньшей вычислительной сложностью (например, алгоритм Страссена ( Strassen’s algorithm )), но эти алгоритмы требуют больших усилий для их освоения, и поэтому в данной лекции при разработке параллельных методов в качестве основы будет использоваться приведенный выше последовательный алгоритм. Также будем предполагать далее, что все матрицы являются квадратными и имеют размер nxn.

7.2. Последовательный алгоритм

Последовательный алгоритм умножения матриц представляется тремя вложенными циклами:

Алгоритм 7.1. Последовательный алгоритм умножения двух квадратных матриц

// Алгоритм 7.1
// Последовательный алгоритм умножения матриц
double MatrixA[Size][Size]; 
double MatrixB[Size][Size];
double MatrixC[Size][Size];
int i,j,k;
...
for (i=0; i<Size; i++){
  for (j=0; j<Size; j++){
    MatrixC[i][j] = 0; 
    for (k=0; k<Size; k++){
      MatrixC[i][j] = MatrixC[i][j] + MatrixA[i][k]*MatrixB[k][j];
    }
  }
}

Этот алгоритм является итеративным и ориентирован на последовательное вычисление строк матрицы С. Действительно, при выполнении одной итерации внешнего цикла (цикла по переменной i ) вычисляется одна строка результирующей матрицы (см. рис. 7.1).

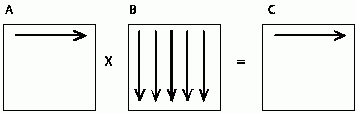
Рис. 7.1. На первой итерации цикла по переменной i используется первая строка матрицы A и все столбцы матрицы B для того, чтобы вычислить элементы первой строки результирующей матрицы С

Поскольку каждый элемент результирующей матрицы есть скалярное произведение строки и столбца исходных матриц, то для вычисления всех элементов матрицы С размером nxn необходимо выполнить n²x(2n–1) скалярных операций и затратить время

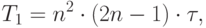( 7.3)

7.3. Умножение матриц при ленточной схеме разделения данных

Рассмотрим два параллельных алгоритма умножения матриц, в которых матрицы A и B разбиваются на непрерывные последовательности строк или столбцов (полосы).

7.3.1. Определение подзадач

Из определения операции матричного умножения следует, что вычисление всех элементов матрицы С может быть выполнено независимо друг от друга. Как результат, возможный подход для организации параллельных вычислений состоит в использовании в качестве базовой подзадачи процедуры определения одного элемента результирующей матрицы С. Для проведения всех необходимых вычислений каждая подзадача должна содержать по одной строке матрицы А и одному столбцу матрицы В. Общее количество получаемых при таком подходе подзадач оказывается равным n² (по числу элементов матрицы С ).

Рассмотрев предложенный подход, можно отметить, что достигнутый уровень параллелизма является в большинстве случаев избыточным. Обычно при проведении практических расчетов такое количество сформированных подзадач превышает число имеющихся процессоров и делает неизбежным этап укрупнения базовых задач. В этом плане может оказаться полезной агрегация вычислений уже на шаге выделения базовых подзадач. Возможное решение может состоять в объединении в рамках одной подзадачи всех вычислений, связанных не с одним, а с несколькими элементами результирующей матрицы С. Для дальнейшего рассмотрения определим базовую задачу как процедуру вычисления всех элементов одной из строк матрицы С. Такой подход приводит к снижению общего количества подзадач до величины n.

Для выполнения всех необходимых вычислений базовой подзадаче должны быть доступны одна из строк матрицы A и все столбцы матрицы B. Простое решение этой проблемы – дублирование матрицы B во всех подзадачах – является, как правило, неприемлемым в силу больших затрат памяти для хранения данных. Поэтому организация вычислений должна быть построена таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть данных, необходимых для проведения расчетов, а доступ к остальной части данных обеспечивался бы при помощи передачи данных между процессорами. Два возможных способа выполнения параллельных вычислений подобного типа рассмотрены далее в п. 7.3.2.

7.3.2. Выделение информационных зависимостей

Для вычисления одной строки матрицы С необходимо, чтобы в каждой подзадаче содержалась строка матрицы А и был обеспечен доступ ко всем столбцам матрицы B. Возможные способы организации параллельных вычислений состоят в следующем.

1. Первый алгоритм. Алгоритм представляет собой итерационную процедуру, количество итераций которой совпадает с числом подзадач. На каждой итерации алгоритма каждая подзадача содержит по одной строке матрицы А и одному столбцу матрицы В. При выполнении итерации проводится скалярное умножение содержащихся в подзадачах строк и столбцов, что приводит к получению соответствующих элементов результирующей матрицы С. По завершении вычислений в конце каждой итерации столбцы матрицы В должны быть переданы между подзадачами с тем, чтобы в каждой подзадаче оказались новые столбцы матрицы В и могли быть вычислены новые элементы матрицы C. При этом данная передача столбцов между подзадачами должна быть организована таким образом, чтобы после завершения итераций алгоритма в каждой подзадаче последовательно оказались все столбцы матрицы В.

Возможная простая схема организации необходимой последовательности передач столбцов матрицы В между подзадачами состоит в представлении топологии информационных связей подзадач в виде кольцевой структуры. В этом случае на каждой итерации подзадача i, 0<=i<n, будет передавать свой столбец матрицы В подзадаче с номером i+1 (в соответствии с кольцевой структурой подзадача n-1 передает свои данные подзадаче с номером 0 ) – см. рис. 7.2. После выполнения всех итераций алгоритма необходимое условие будет обеспечено – в каждой подзадаче поочередно окажутся все столбцы матрицы В.

На рис. 7.2 представлены итерации алгоритма матричного умножения для случая, когда матрицы состоят из четырех строк и четырех столбцов ( n=4 ). В начале вычислений в каждой подзадаче i, 0<=i<n, располагаются i -я строка матрицы A и i -й столбец матрицы B. В результате их перемножения подзадача получает элемент c_ii результирующей матрицы С. Далее подзадачи осуществляют обмен столбцами, в ходе которого каждая подзадача передает свой столбец матрицы B следующей подзадаче в соответствии с кольцевой структурой информационных взаимодействий. Далее выполнение описанных действий повторяется до завершения всех итераций параллельного алгоритма.

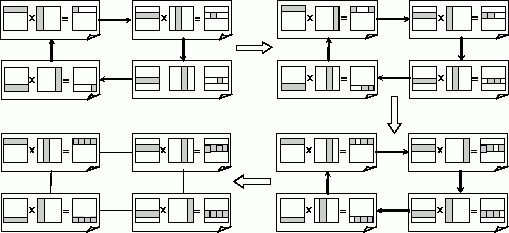
Рис. 7.2. Общая схема передачи данных для первого параллельного алгоритма матричного умножения при ленточной схеме разделения данных

2. Второй алгоритм. Отличие второго алгоритма состоит в том, что в подзадачах располагаются не столбцы, а строки матрицы B. Как результат, перемножение данных каждой подзадачи сводится не к скалярному умножению имеющихся векторов, а к их поэлементному умножению. В результате подобного умножения в каждой подзадаче получается строка частичных результатов для матрицы C.

При рассмотренном способе разделения данных для выполнения операции матричного умножения нужно обеспечить последовательное получение в подзадачах всех строк матрицы B, поэлементное умножение данных и суммирование вновь получаемых значений с ранее вычисленными результатами. Организация необходимой последовательности передач строк матрицы B между подзадачами также может быть выполнена с использованием кольцевой структуры информационных связей (см. рис. 7.3).

На рис. 7.3 представлены итерации алгоритма матричного умножения для случая, когда матрицы состоят из четырех строк и четырех столбцов ( n=4 ). В начале вычислений в каждой подзадаче i, 0<=i<n, располагаются i -е строки матрицы A и матрицы B. В результате их перемножения подзадача определяет i -ю строку частичных результатов искомой матрицы C. Далее подзадачи осуществляют обмен строками, в ходе которого каждая подзадача передает свою строку матрицы B следующей подзадаче в соответствии с кольцевой структурой информационных взаимодействий. Далее выполнение описанных действий повторяется до завершения всех итераций параллельного алгоритма.

Рис. 7.3. Общая схема передачи данных для второго параллельного алгорится матричного умножения при ленточной схеме разделения данных