Параллельные методы матричного умножения
7.4. Алгоритм Фокса умножения матриц при блочном разделении данных
При построении параллельных способов выполнения матричного умножения наряду с рассмотрением матриц в виде наборов строк и столбцов широко используется блочное представление матриц. Рассмотрим более подробно данный способ организации вычислений.
7.4.1. Определение подзадач
Блочная схема разбиения матриц подробно изложена в первом разделе "Параллельные методы умножения матрицы на вектор" . При таком способе разделения данных исходные матрицы А, В и результирующая матрица С представляются в виде наборов блоков. Для более простого изложения следующего материала будем предполагать далее, что все матрицы являются квадратными размера nxn, количество блоков по горизонтали и вертикали одинаково и равно q (т.е. размер всех блоков равен kxk, k=n/q ). При таком представлении данных операция матричного умножения матриц А и B в блочном виде может быть представлена так:
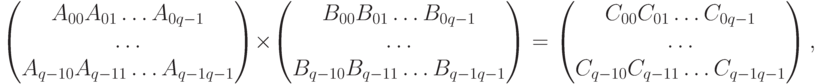
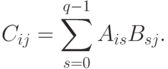
При блочном разбиении данных для определения базовых подзадач естественным представляется взять за основу вычисления, выполняемые над матричными блоками. С учетом сказанного определим базовую подзадачу как процедуру вычисления всех элементов одного из блоков матрицы С.
Для выполнения всех необходимых вычислений базовым подзадачам должны быть доступны соответствующие наборы строк матрицы A и столбцов матрицы B. Размещение всех требуемых данных в каждой подзадаче неизбежно приведет к дублированию и к значительному росту объема используемой памяти. Как результат, вычисления должны быть организованы таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть необходимых для проведения расчетов данных, а доступ к остальной части данных обеспечивался бы при помощи передачи данных между процессорами. Один из возможных подходов – алгоритм Фокса ( Fox ) – рассмотрен далее в данном подразделе. Второй способ – алгоритм Кэннона ( Cannon ) – приводится в подразделе 7.5.
7.4.2. Выделение информационных зависимостей
Итак, за основу параллельных вычислений для матричного умножения при блочном разделении данных принят подход, при котором базовые подзадачи отвечают за вычисления отдельных блоков матрицы C и при этом в подзадачах на каждой итерации расчетов располагается только по одному блоку исходных матриц A и B. Для нумерации подзадач будем использовать индексы размещаемых в подзадачах блоков матрицы C, т.е. подзадача (i,j) отвечает за вычисление блока Cij – тем самым, набор подзадач образует квадратную решетку, соответствующую структуре блочного представления матрицы C.
Возможный способ организации вычислений при таких условиях состоит в применении широко известного алгоритма Фокса ( Fox ) — см., например, [ [ 34 ] , [ 51 ] ].
В соответствии с алгоритмом Фокса в ходе вычислений на каждой базовой подзадаче (i,j) располагается четыре матричных блока:
- блок Cij матрицы C, вычисляемый подзадачей;
- блок Aij матрицы A, размещаемый в подзадаче перед началом вычислений;
- блоки A'ij, B'ij матриц A и B, получаемые подзадачей в ходе выполнения вычислений.
Выполнение параллельного метода включает:
- этап инициализации, на котором каждой подзадаче (i,j) передаются блоки Aij, Bij и обнуляются блоки Cij на всех подзадачах;
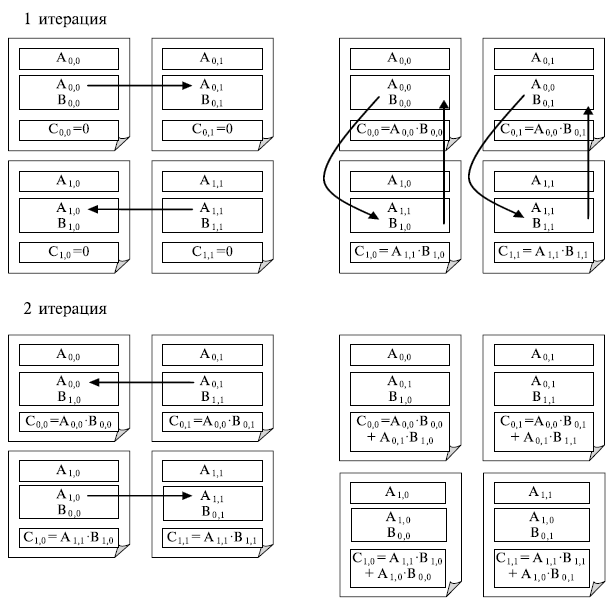
- этап вычислений, в рамках которого на каждой итерации l, 0<=l<q, осуществляются следующие операции:
- для каждой строки i, 0<=i<q, блок Aij подзадачи (i,j)
пересылается на все подзадачи той же строки i решетки; индекс j,
определяющий положение подзадачи в строке, вычисляется в
соответствии с выражениемгде mod есть операция получения остатка от целочисленного деления;
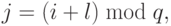
- полученные в результаты пересылок блоки A'ij, B'ij каждой подзадачи (i,j) перемножаются и прибавляются к блоку Cij
- блоки B'ij каждой подзадачи (i,j) пересылаются подзадачам, являющимся соседями сверху в столбцах решетки подзадач (блоки подзадач из первой строки решетки пересылаются подзадачам последней строки решетки).
Для пояснения этих правил параллельного метода на рис. 7.6 приведено состояние блоков в каждой подзадаче в ходе выполнения итераций этапа вычислений (для решетки подзадач 2x2 ).
7.4.3. Масштабирование и распределение подзадач по процессорам
В рассмотренной схеме параллельных вычислений количество
блоков может варьироваться в зависимости от выбора размера блоков
– эти размеры могут быть подобраны таким образом, чтобы общее
количество базовых подзадач совпадало с числом процессоров p.
Так, например, в наиболее простом случае, когда число процессоров
представимо в виде 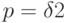 (т.е. является полным квадратом), можно
выбрать количество блоков в матрицах по вертикали и горизонтали
равным
(т.е. является полным квадратом), можно
выбрать количество блоков в матрицах по вертикали и горизонтали
равным  (т.е.
(т.е.  ). Такой способ определения количества блоков
приводит к тому, что объем вычислений в каждой подзадаче является
одинаковым и тем самым достигается полная балансировка
вычислительной нагрузки между процессорами. В более общем случае
при произвольных количестве процессоров и размерах матриц
балансировка вычислений может отличаться от абсолютно одинаковой,
но, тем не менее, при надлежащем выборе параметров может быть
распределена между процессорами равномерно в рамках требуемой
точности.
). Такой способ определения количества блоков
приводит к тому, что объем вычислений в каждой подзадаче является
одинаковым и тем самым достигается полная балансировка
вычислительной нагрузки между процессорами. В более общем случае
при произвольных количестве процессоров и размерах матриц
балансировка вычислений может отличаться от абсолютно одинаковой,
но, тем не менее, при надлежащем выборе параметров может быть
распределена между процессорами равномерно в рамках требуемой
точности.
Для эффективного выполнения алгоритма Фокса, в котором базовые подзадачи представлены в виде квадратной решетки и в ходе вычислений выполняются операции передачи блоков по строкам и столбцам решетки подзадач, наиболее адекватным решением является организация множества имеющихся процессоров также в виде квадратной решетки. В этом случае можно осуществить непосредственное отображение набора подзадач на множество процессоров – базовую подзадачу (i,j) следует располагать на процессоре Pi,j. Необходимая структура сети передачи данных может быть обеспечена на физическом уровне, если топология вычислительной системы имеет вид решетки или полного графа.
7.4.4. Анализ эффективности
Определим вычислительную сложность данного алгоритма Фокса. Построение оценок будет происходить при условии выполнения всех ранее выдвинутых предположений: все матрицы являются квадратными размера nxn, количество блоков по горизонтали и вертикали являются одинаковым и равным q (т.е. размер всех блоков равен kxk, k=n/q ), процессоры образуют квадратную решетку и их количество равно p=q2.
Как уже отмечалось, алгоритм Фокса требует для своего выполнения q итераций, в ходе которых каждый процессор перемножает свои текущие блоки матриц А и В и прибавляет результаты умножения к текущему значению блока матрицы C. С учетом выдвинутых предположений общее количество выполняемых при этом операций будет иметь порядок n3/p. Как результат, показатели ускорения и эффективности алгоритма имеют вид:
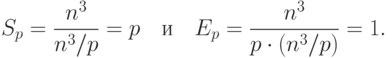 |
( 7.9) |
Общий анализ сложности снова дает идеальные показатели эффективности параллельных вычислений. Уточним полученные соотношения — для этого укажем более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
Определим количество вычислительных операций. Сложность выполнения скалярного умножения строки блока матрицы A на столбец блока матрицы В можно оценить как 2(n/q)-1. Количество строк и столбцов в блоках равно n/q и, как результат, трудоемкость операции блочного умножения оказывается равной (n2/p)(2n/q-1). Для сложения блоков требуется n2/p операций. С учетом всех перечисленных выражений время выполнения вычислительных операций алгоритма Фокса может быть оценено следующим образом:
![T_p(calc)=q[(n^2 /p)\cdot(2n/q-1)+(n^2 /p)]\cdot\tau.](/sites/default/files/tex_cache/80440db2fe6cf4161896c259fa647482.png) |
( 7.10) |
 есть время выполнения одной элементарной скалярной операции).
есть время выполнения одной элементарной скалярной операции).Оценим затраты на выполнение операций передачи данных между процессорами. На каждой итерации алгоритма перед умножением блоков один из процессоров строки процессорной решетки рассылает свой блок матрицы A остальным процессорам своей строки. Как уже отмечалось ранее, при топологии сети в виде гиперкуба или полного графа выполнение этой операции может быть обеспечено за log2q шагов, а объем передаваемых блоков равен n2/p. Как результат, время выполнения операции передачи блоков матрицы A при использовании модели Хокни может оцениваться как
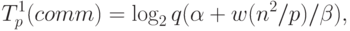 |
( 7.11) |
 – латентность,
– латентность,  – пропускная способность сети
передачи данных, а w есть размер элемента матрицы в байтах. В
случае же когда топология строк процессорной решетки представляет
собой кольцо, выражение для оценки времени передачи блоков
матрицы A принимает вид:
– пропускная способность сети
передачи данных, а w есть размер элемента матрицы в байтах. В
случае же когда топология строк процессорной решетки представляет
собой кольцо, выражение для оценки времени передачи блоков
матрицы A принимает вид: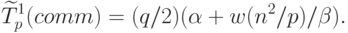
Далее после умножения матричных блоков процессоры передают свои блоки матрицы В предыдущим процессорам по столбцам процессорной решетки (первые процессоры столбцов передают свои данные последним процессорам в столбцах решетки). Эти операции могут быть выполнены процессорами параллельно, и, тем самым, длительность такой коммуникационной операции составляет:
 |
( 7.12) |
Просуммировав все полученные выражения, можно получить, что общее время выполнения алгоритма Фокса может быть определено при помощи следующих соотношений:
![\begin{aligned}
T_p &= q[(n^2/p) \cdot (2n/q-1)+(n^2/p)] \cdot \tau+q \log_2 q(\alpha + w(n^2/p)/ \beta) + \\
&+(q-1) \cdot (\alpha + w(n^2/p)/ \beta) = q[(n^2/p) \cdot (2n/q-1)+(n^2/p)] \cdot \tau+ \\
&+(q\log_2 q +(q-1))( \alpha + w(n^2/p)/ \beta)
\end{aligned}](/sites/default/files/tex_cache/36ba45f996d40ccac4f9381a91783fbf.png) |
( 7.13) |
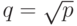 ).
).