Параллельные методы умножения матрицы на вектор
Матрицы и матричные операции широко используются при математическом моделировании самых разнообразных процессов, явлений и систем. Матричные вычисления составляют основу многих научных и инженерных расчетов – среди областей приложений могут быть указаны вычислительная математика, физика, экономика и др.
С учетом значимости эффективного выполнения матричных расчетов многие стандартные библиотеки программ содержат процедуры для различных матричных операций. Объем программного обеспечения для обработки матриц постоянно увеличивается – разрабатываются новые экономные структуры хранения для матриц специального типа (треугольных, ленточных, разреженных и т.п.), создаются различные высокоэффективные машинно-зависимые реализации алгоритмов, проводятся теоретические исследования для поиска более быстрых методов матричных вычислений.
Являясь вычислительно трудоемкими, матричные вычисления представляют собой классическую область применения параллельных вычислений. С одной стороны, использование высокопроизводительных многопроцессорных систем позволяет существенно повысить сложность решаемых задач. С другой стороны, в силу своей достаточно простой формулировки матричные операции предоставляют прекрасную возможность для демонстрации многих приемов и методов параллельного программирования.
В данной лекции обсуждаются методы параллельных вычислений для операции матрично-векторного умножения, в следующей лекции ( "Параллельные методы матричного умножения" ) излагается более общий случай – задача перемножения матриц. Важный вид матричных вычислений – решение систем линейных уравнений – представлен в "Решение систем линейных уравнений" . Общий для всех перечисленных задач вопрос разделения обрабатываемых матриц между параллельно работающими процессорами рассматривается в первом подразделе лекции 6.
При изложении следующего материала будем полагать, что рассматриваемые матрицы являются плотными ( dense ), то есть число нулевых элементов в них незначительно по сравнению с общим количеством элементов матриц.
6.1. Принципы распараллеливания
Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данное свойство свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов, и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами используемой вычислительной системы. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений; существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.
Наиболее общие и широко используемые способы разделения матриц состоят в разбиении данных на полосы (по вертикали или горизонтали) или на прямоугольные фрагменты ( блоки ).
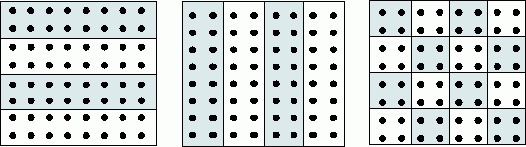
1. Ленточное разбиение матрицы. При ленточном ( block-striped ) разбиении каждому процессору выделяется то или иное подмножество строк ( rowwise или горизонтальное разбиение ) или столбцов ( columnwise или вертикальное разбиение ) матрицы (рис. 6.1). Разделение строк и столбцов на полосы в большинстве случаев происходит на непрерывной ( последовательной ) основе. При таком подходе для горизонтального разбиения по строкам, например, матрица A представляется в виде (см. рис. 6.1)
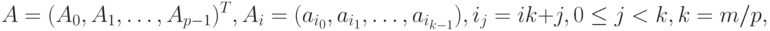 |
( 6.1) |
Другой возможный подход к формированию полос состоит в применении той или иной схемы чередования ( цикличности ) строк или столбцов. Как правило, для чередования используется число процессоров p – в этом случае при горизонтальном разбиении матрица A принимает вид
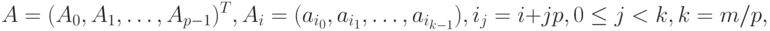 |
( 6.2) |
Циклическая схема формирования полос может оказаться полезной для лучшей балансировки вычислительной нагрузки процессоров (например, при решении системы линейных уравнений с использованием метода Гаусса – см. "Решение систем линейных уравнений" ).
2. Блочное разбиение матрицы. При блочном ( chessboard block ) разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p = sxq, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m = kxs и n = lxq. Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:

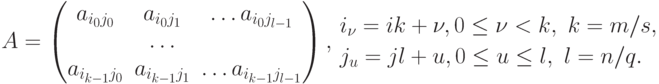 |
( 6.3) |
При таком подходе целесообразно, чтобы вычислительная система имела физическую или, по крайней мере, логическую топологию процессорной решетки из s строк и q столбцов. В этом случае при разделении данных на непрерывной основе процессоры, соседние в структуре решетки, обрабатывают смежные блоки исходной матрицы. Следует отметить, однако, что и для блочной схемы может быть применено циклическое чередование строк и столбцов.
В данной лекции рассматриваются три параллельных алгоритма для умножения квадратной матрицы на вектор. Каждый подход основан на разном типе распределения исходных данных (элементов матрицы и вектора) между процессорами. Разделение данных меняет схему взаимодействия процессоров, поэтому каждый из представленных методов существенным образом отличается от двух остальных.