Параллельные методы умножения матрицы на вектор

6.5.5. Результаты вычислительных экспериментов

Рассмотрим результаты вычислительных экспериментов, выполненных для оценки эффективности приведенного выше параллельного алгоритма умножения матрицы на вектор. Кроме того, используем полученные результаты для сравнения теоретических оценок и экспериментальных показателей времени вычислений и проверим тем самым точность полученных аналитических соотношений. Эксперименты проводились на вычислительном кластере Нижегородского университета на базе процессоров Intel Xeon 4 EM64T, 3000 МГц и сети Gigabit Ethernet под управлением операционной системы Microsoft Windows Server 2003 Standard x64 Edition и системы управления кластером Microsoft Compute Cluster Server (см. п. 1.2.3).

Определение параметров теоретических зависимостей (величин 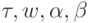) осуществлялось следующим образом. Для оценки длительности базовой скалярной операции проводилось решение задачи умножения матрицы на вектор при помощи последовательного алгоритма и полученное таким образом время вычислений делилось на общее количество выполненных операций – в результате подобных экспериментов для величины было получено значение 1,93 нсек. Эксперименты, выполненные для определения параметров сети передачи данных, показали значения латентности и пропускной способности соответственно 47 мкс и 53,29 Мбайт/с. Все вычисления производились над числовыми значениями типа double, т.е. величина w равна 8 байт.

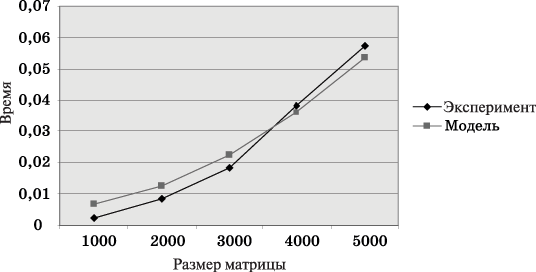
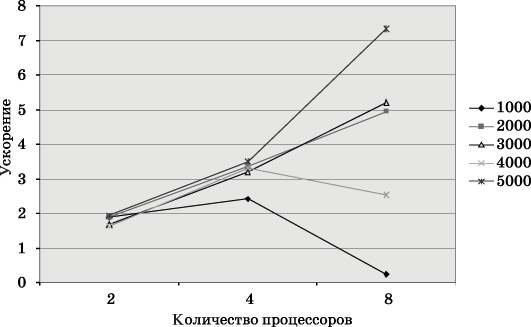
Результаты вычислительных экспериментов приведены в таблице 6.1. Эксперименты проводились с использованием двух, четырех и восьми процессоров. Времена выполнения алгоритмов указаны в секундах.

Сравнение экспериментального времени 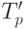выполнения параллельного алгоритма и теоретического времени T_p, вычисленного в соответствии с выражением (6.8), представлено в таблице 6.2 и в графическом виде на рис. 6.3 и 6.4.

Рис. 6.3. График зависимости экспериментального T'p и теоретического Tp времени выполнения параллельного алгоритма на двух процессорах от объема исходных данных (ленточное разбиение матрицы по строкам)

Рис. 6.4. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма умножения матрицы на вектор (ленточное разбиение по строкам) для разных размеров матриц