Быстрые квантовые алгоритмы
Построение измеряющего оператора.
Теперь будем строить оператор, измеряющий собственные числа 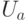 . Как уже было сказано, можно ограничиться изучением действия этого оператора на вход
. Как уже было сказано, можно ограничиться изучением действия этого оператора на вход 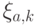 . Построение разделяется на три этапа.
. Построение разделяется на три этапа.
- Ищем информацию о
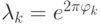 , где .
, где .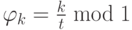
- Локализуем значение
 с небольшой точностью. Самое время подчеркнуть, что во всех приводимых рассуждениях есть два параметра: вероятность ошибки
с небольшой точностью. Самое время подчеркнуть, что во всех приводимых рассуждениях есть два параметра: вероятность ошибки 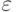 и точность
и точность  . Мы получаем некоторое число
. Мы получаем некоторое число  как результат измерения, при этом должно выполняться условие
как результат измерения, при этом должно выполняться условие ![\Prob[|z-\ph_k|>\delta]\le\eps](/sites/default/files/tex_cache/7e9f1fa45b682237f2a20155a2c71f89.png) . Пока нас устроит небольшая точность, скажем,
. Пока нас устроит небольшая точность, скажем, 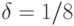
- Далее нужно увеличить точность. Необходимо уметь отличать друг от друга числа вида
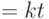 , где
, где 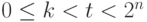 . Заметим, что если
. Заметим, что если 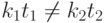 , то
, то  . Поэтому, зная значение
. Поэтому, зная значение  с точностью
с точностью  , мы можем определить его абсолютно точно (в виде несократимой дроби). Чтобы сделать это эффективно (за полиномиальное время), можно использовать алгоритм цепных дробей.
, мы можем определить его абсолютно точно (в виде несократимой дроби). Чтобы сделать это эффективно (за полиномиальное время), можно использовать алгоритм цепных дробей.
Как получать информацию о собственном числе.
В
"Измеряющие операторы"
был введен оператор 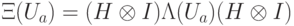 , измеряющий собственные числа. В нашем случае
, измеряющий собственные числа. В нашем случае 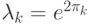 , поэтому можно записать этот оператор в виде
, поэтому можно записать этот оператор в виде
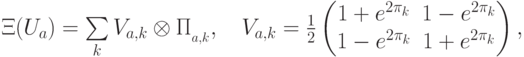
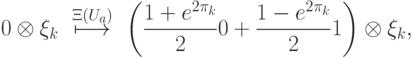
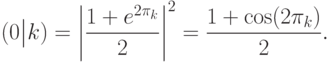
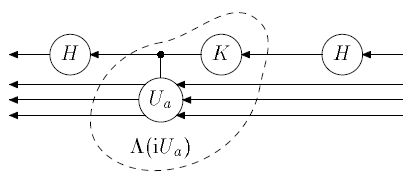
Нам потребуется еще оператор 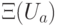 . Его также нетрудно реализовать. Реализация, изображенная на рисунке, использует оператор
. Его также нетрудно реализовать. Реализация, изображенная на рисунке, использует оператор 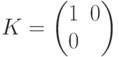 из стандартного базиса. Обведенный фрагмент реализует оператор
из стандартного базиса. Обведенный фрагмент реализует оператор 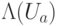 . Действительно,
. Действительно,  умножает на
умножает на  только
только 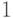 , но как раз в этом случае применяется оператор
, но как раз в этом случае применяется оператор 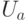 (по определению оператора
(по определению оператора 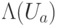 ). Для оператора
). Для оператора 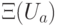 условные вероятности равны
условные вероятности равны
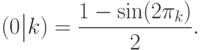
Сложность реализации операторов 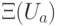 и
и 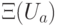 зависит от сложности реализации оператора
зависит от сложности реализации оператора 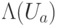 , которая ненамного выше сложности реализации оператора
, которая ненамного выше сложности реализации оператора 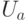 (см. задачу 12.2).
(см. задачу 12.2).
Оценка условных вероятностей.
Мы будем локализовывать значение 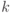 , оценивая условные вероятности, приведенные выше. Для получения такой оценки будем применять операторы
, оценивая условные вероятности, приведенные выше. Для получения такой оценки будем применять операторы 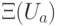 и
и 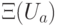 к различным "приборам" (дополнительным q-битам). Рассуждения одинаковы для обоих операторов, поэтому ограничимся случаем
к различным "приборам" (дополнительным q-битам). Рассуждения одинаковы для обоих операторов, поэтому ограничимся случаем 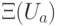 .
.
У нас есть квантовый регистр  , в котором находится
, в котором находится 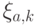 . (На самом деле там вначале был
. (На самом деле там вначале был
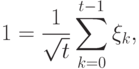
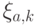 по отдельности; это корректно в силу вида измеряющего оператора). Заведем большое количество (
по отдельности; это корректно в силу вида измеряющего оператора). Заведем большое количество (  штук) вспомогательных регистров длиной в 1 бит. Каждый из этих регистров будет использоваться для применения оператора
штук) вспомогательных регистров длиной в 1 бит. Каждый из этих регистров будет использоваться для применения оператора 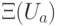 .
.Как было доказано в "Измеряющие операторы" , условные вероятности в таком случае перемножаются. Для оператора
![\prod\limits_{r=1}^s \Xi(U_a)[r,A]](/sites/default/files/tex_cache/58682576919d4b606ee3f6e0c44dddf5.png)
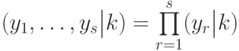 (здесь через
(здесь через 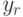 обозначено значение в
обозначено значение в  -ом бите).
-ом бите).Далее с битами, в которых записаны результаты "экспериментов", будут уже производиться классические действия. Поскольку условные вероятности перемножаются, можно считать, что мы оцениваем вероятность выпадения 1 в серии испытаний Бернулли.
Если монета брошена  раз, то доля выпавших единиц
раз, то доля выпавших единиц 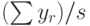 примерно равна
примерно равна 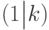 . С какой точностью верна такая оценка? Из теории вероятностей известно, что
. С какой точностью верна такая оценка? Из теории вероятностей известно, что
![\Prob\left[\left|\frac{\sum\nolimits_{r=1}^{s}y_r}{s}-\PP(1\big|k)\right| >\delta\right]<2e^{-c\delta^{2}s},](/sites/default/files/tex_cache/12136d3feb30efbf5dbb82aeee0c0592.png)
 — некоторая константа. Это показывает, что при любом фиксированном
— некоторая константа. Это показывает, что при любом фиксированном  можно добиться вероятности ошибки
можно добиться вероятности ошибки 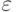 за
за 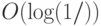 испытаний.
испытаний.Итак, мы научились находить с некоторой точностью  синус и косинус от
синус и косинус от 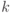 . Теперь подберем
. Теперь подберем  таким, чтобы значение
таким, чтобы значение 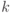 можно было установить по значениям синуса и косинуса с точностью
можно было установить по значениям синуса и косинуса с точностью 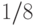 . На этом второй этап завершен.
. На этом второй этап завершен.