Быстрые квантовые алгоритмы
Разложение на множители и нахождение периода относительно возведения в степень.
Второе свидетельство в пользу гипотезы 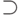 — быстрые квантовые алгоритмы разложения числа на простые множители и вычисления дискретного логарифма. Они были найдены П. Шором [38]. Обсудим пока первую из этих двух задач.
— быстрые квантовые алгоритмы разложения числа на простые множители и вычисления дискретного логарифма. Они были найдены П. Шором [38]. Обсудим пока первую из этих двух задач.
Факторизация числа. Дано натуральное число  . Требуется найти его разложение на простые множители
. Требуется найти его разложение на простые множители
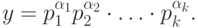
Эта задача считается сложной настолько, что на предположении о трудности ее решения основываются практические алгоритмы криптографии. С теоретической точки зрения положение несколько хуже: неизвестно ни сведение к задаче факторизации задач из класса NP, ни другие "прямые" свидетельства в пользу ее сложности. (Слово "прямые" взято в кавычки из-за того, что в настоящее время неизвестен ответ на вопрос  .) Таким образом, предположение о сложности задачи факторизации пополняет и без того обильную коллекцию недоказанных гипотез в вычислительной теории сложности. Количество таких гипотез хочется по возможности уменьшать. В этом и состоит основная ценность результата Шора — если совершить один "акт веры" и уверовать в сложность задачи факторизации, то необходимость в еще одном акте веры (относительно больших вычислительных возможностей квантового компьютера) отпадает.
.) Таким образом, предположение о сложности задачи факторизации пополняет и без того обильную коллекцию недоказанных гипотез в вычислительной теории сложности. Количество таких гипотез хочется по возможности уменьшать. В этом и состоит основная ценность результата Шора — если совершить один "акт веры" и уверовать в сложность задачи факторизации, то необходимость в еще одном акте веры (относительно больших вычислительных возможностей квантового компьютера) отпадает.
Мы будем строить быстрый квантовый алгоритм не для решения задачи факторизации, а для решения другой задачи Нахождение периода, к которой задача факторизации сводится с помощью классического вероятностного алгоритма.
Нахождение периода. Имеется число  , записывающееся не более чем
, записывающееся не более чем  двоичными цифрами (
двоичными цифрами ( 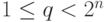 ) и число
) и число  такое, что
такое, что 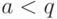 ,
, 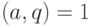 (
( 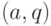 обозначает наибольший общий делитель). Нужно найти период
обозначает наибольший общий делитель). Нужно найти период  относительно
относительно  , т.е. такое наименьшее неотрицательное число
, т.е. такое наименьшее неотрицательное число  , что
, что  .
.
Другими словами, период — это порядок числа  в мультипликативной группе вычетов
в мультипликативной группе вычетов 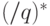 . Будем обозначать период числа
. Будем обозначать период числа  относительно
относительно  как
как 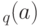 .
.
Ниже мы построим квантовый алгоритм для решения задачи о нахождении периода числа. Но начнем с того, что опишем классическое вероятностное сведение задачи факторизации к задаче вычисления периода. Читателю также предлагается вспомнить вероятностный тест простоты числа, изложенный в первой части (см. "Вероятностные алгоритмы и класс BPP. Проверка простоты числа" ).
Сведение факторизации к вычислению периода.
Итак, предположим, что мы умеем решать задачу нахождения периода. Ясно, что факторизацию числа  можно получить, используя
можно получить, используя  раз подпрограмму, которая по любому составному числу вычисляет какой-то его делитель с вероятностью, не меньшей
раз подпрограмму, которая по любому составному числу вычисляет какой-то его делитель с вероятностью, не меньшей 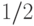 . (Конечно, нужна также стандартная процедура усиления вероятностей, описанная в
"Вероятностные алгоритмы и класс BPP. Проверка простоты числа"
.)
. (Конечно, нужна также стандартная процедура усиления вероятностей, описанная в
"Вероятностные алгоритмы и класс BPP. Проверка простоты числа"
.)
Процедура нахождения делителя.
Вход: число  .
.
Шаг 1. Проверяем четность  . Если
. Если  — четное, то выдаем ответ "2", в противном случае переходим к шагу 2.
— четное, то выдаем ответ "2", в противном случае переходим к шагу 2.
Шаг 2. Проверяем, извлекается ли из  нацело корень
нацело корень  -й степени при
-й степени при 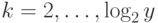 . Если
. Если 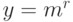 , то ответ "
, то ответ "  ", иначе переходим к шагу 3.
", иначе переходим к шагу 3.
Шаг 3. Выбираем случайное  среди чисел от
среди чисел от  до
до  , вычисляем
, вычисляем 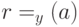 (используя имеющийся по предположению алгоритм нахождения периода) и, если
(используя имеющийся по предположению алгоритм нахождения периода) и, если  — нечетное, то ответ "
— нечетное, то ответ "  — простое". В противном случае находим
— простое". В противном случае находим 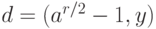 (скажем, алгоритмом Евклида) и переходим к шагу 4.
(скажем, алгоритмом Евклида) и переходим к шагу 4.
Шаг 4. Если  , то ответ "
, то ответ "  ", в противном случае ответ "
", в противном случае ответ "  — простое".
— простое".
Анализ процедуры нахождения делителя.
Докажем, что вероятность получить делитель числа  в результате работы процедуры нахождения делителя не меньше, чем
в результате работы процедуры нахождения делителя не меньше, чем  , где
, где  — число различных простых делителей
— число различных простых делителей  . (Заметим, в частности, что эта вероятность равна~0 для простого
. (Заметим, в частности, что эта вероятность равна~0 для простого  , так что данная процедура может также использоваться и как тест простоты числа.) При доказательстве нам потребуется китайская теорема об остатках и тот факт, что мультипликативная группа вычетов по модулю
, так что данная процедура может также использоваться и как тест простоты числа.) При доказательстве нам потребуется китайская теорема об остатках и тот факт, что мультипликативная группа вычетов по модулю 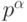 , где
, где  простое, — циклическая (см. [2, Гл. 6, 3]).
простое, — циклическая (см. [2, Гл. 6, 3]).
Если 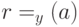 — четное, то
— четное, то 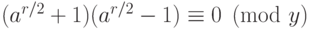 . Так что в этом случае процедура выдаст ответ "
. Так что в этом случае процедура выдаст ответ "  — простое" только тогда, когда
— простое" только тогда, когда 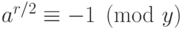 .
.
Запишем разложение  на простые множители
на простые множители  и введем обозначения
и введем обозначения
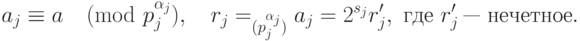
Докажем, что процедура выдает ответ "  — простое" тогда и только тогда, когда
— простое" тогда и только тогда, когда 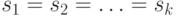 . Действительно, если
. Действительно, если 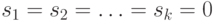 , то
, то  нечетно (поскольку
нечетно (поскольку  — наименьшее общее кратное всех
— наименьшее общее кратное всех 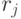 ). Если
). Если 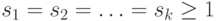 , то
, то 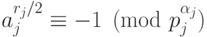 (используем цикличность
(используем цикличность 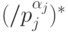 ), а, значит, и
), а, значит, и 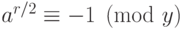 (используем китайскую теорему об остатках). Наоборот, если не все
(используем китайскую теорему об остатках). Наоборот, если не все 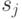 равны, то при некотором
равны, то при некотором  получим
получим  , т.е.
, т.е. 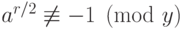 .
.
По китайской теореме об остатках случайный равномерный выбор  есть то же самое, что независимый случайный равномерный выбор всех
есть то же самое, что независимый случайный равномерный выбор всех 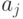 . Оценим для некоторого
. Оценим для некоторого  вероятность события
вероятность события 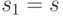 при независимом выборе
при независимом выборе  . Пусть
. Пусть 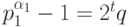 , где
, где  — нечетное,
— нечетное,  — образующая (циклической) группы
— образующая (циклической) группы 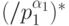 . Тогда
. Тогда

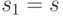 не больше
не больше 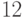 . Отсюда следует искомая оценка вероятности успеха всей процедуры нахождения делителя: вероятность события
. Отсюда следует искомая оценка вероятности успеха всей процедуры нахождения делителя: вероятность события 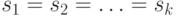 не выше
не выше 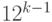 , поэтому с вероятностью не меньше
, поэтому с вероятностью не меньше  процедура нахождения делителя найдет делитель
процедура нахождения делителя найдет делитель  .
.