НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 11: Измеряющие операторы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 617 / 28 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В этой рассматривается особый класс операторов - измеряющий оператор, а также подробно описываются его свойства. Кроме того в лекции подробно рассмотрен пример прикладного использования измеряющего оператора для исследования физических явлений, а также его математическое обоснование.

Ключевые слова: класс, пространство состояний, состояние системы, базис, матрица, ПО, вектор

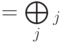Введем особый класс операторов — измеряющие операторы. Пусть есть пространство состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ . Тогда всякий оператор вида 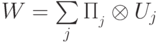$W=\sum\limits_{j}^{} \Pi_{\calL_j}\otimes U_j$ будем называть измеряющим.

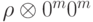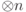Чтобы оправдать такое название, рассмотрим следующий процесс. Пусть имеется некоторое состояние, описываемое матрицей плотности $\rho\in\LL(\calN)$ . Подсоединим прибор ; совместное состояние системы и прибора описывается матрицей плотности $\rho\otimes\ket{0^m}\bra{0^m}$ (мы считаем, что во втором сомножителе, описывающем прибор, есть выделенный базис, например, что это $\BB^{\otimes n}$ ).

Теперь применяем измеряющий оператор . Получаем состояние

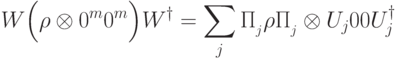
$W\Bigl(\rho\otimes\ket{0^m}\bra{0^m}\Bigr)W^\dagger =\sum_{j}^{}\Pi_{\calL_j}\rho\Pi_{\calL_j}\otimes U_j\ket{0}\bra{0}U_j^\dagger$

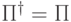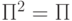(здесь мы воспользовались характеристическими свойствами проектора $\Pi^\dagger=\Pi$ , $\Pi^2=\Pi$ ).

И последнее действие: прибор становится классическим. Это означает, что матрица диагонализуется по второму сомножителю. Посмотрим, во что переходят при этом вторые сомножители в написанной сумме:

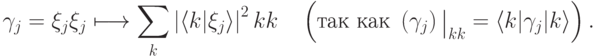
$\gamma_j=\ket{\xi_j}\bra{\xi_j} \longmapsto \sum_{k}^{} \left| \langle k|\xi_j\rangle\right|^2 \ket{k}\bra{k} \quad\left(\text{так как } \left(\gamma_j\right)\raisebox{-2pt}{\big|}_{kk} = \langle k|\gamma_j|k\rangle\right).$

Теперь запишем получившийся результат:

$\sum_{j}^{}\sum_{k}^{}\left(\Pi_{\calL_j}\rho\Pi_{\calL_j} \left|\langle k|U_j|0\rangle \right|^2,\,k\right) = \sum_{j}^{}\sum_{k}^{}\PP(k\big|j)\left(\Pi_{\calL_j}\rho\Pi_{\calL_j}, k\right),$

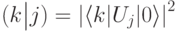где введены условные вероятности $\PP(k\big|j) = \left|\langle k|U_j|0\rangle \right|^2$ . Заметим, что для измерения (как оно было определено в предыдущем разделе) 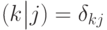$\PP(k\big|j)=\delta_{kj}$ , поэтому только что описанный процесс можно назвать "вероятностным измерением". Введенные таким образом квантовые условные вероятности ведут себя как обычные, если рассматриваются произведения измеряющих операторов, построенных на одном и том же ортогональном разложении пространства состояний (см. ниже).

Приведем примеры измеряющих операторов.

1. Оператор $\Lambda(U)=\Pi_0\otimes I + \Pi_1\otimes U$ , действующий на пространстве $\BB\otimes \calN$ , — измеряющий.

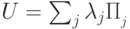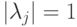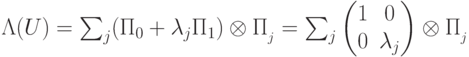1'. Нетривиально, что он измеряющий и по второй компоненте. Поскольку — унитарный оператор, его можно разложить в сумму проекторов на собственные подпространства: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ . Тогда $\Lambda(U)=\sum_{j} (\Pi_0+\lambda_j\Pi_1)\otimes\Pi_{\calL_j}= \sum_{j}^{} \begin{pmatrix} 1&0\\ 0&\lambda_j \end{pmatrix} \otimes\Pi_{\calL_j}$ . 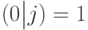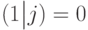В этом случае условные вероятности равны $\PP(0\big|j) =1$ и $\PP(1\big|j) =0$ , поэтому такой оператор, хотя и является измеряющим по определению, фактически ничего не измеряет.

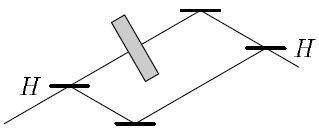
Замечание для физиков. Пусть — оператор фазового сдвига света при прохождении сквозь стеклянную пластинку. Мы можем разделить луч света на два, пропустив его через полупрозрачное зеркало, затем один из полученных лучей пропустить через стеклянную пластинку, а затем заставить полученные в результате лучи интерферировать. По картине интерференции можно узнать фазовый сдвиг.

Математический вариант предыдущего примера. Аналогом полупрозрачного зеркала будет служить оператор

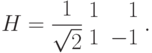
$H=\displaystyle\frac{1}{\sqrt2} \leftp\begin{array}{rr}1&1\\1&-1\end{array}\rightp.$

Как видно из приведенной выше картинки, его нужно применить в начале и в конце. Строго говоря, рассмотрим оператор

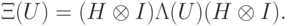
$\Xi(U)=(H\otimes I)\Lambda(U)(H\otimes I).$

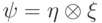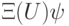
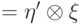Если начальный вектор имеет вид $\ket{\psi}=\ket{\eta}\otimes\ket{\xi}$ ( $\ket{\xi}\in\calL_j$ ), то $\Xi(U)\ket{\psi}$ $=\ket{\eta'}\otimes\ket{\xi}$ , где

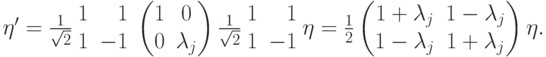
$\ket{\eta'}=\frac{1}{\sqrt2} \leftp\begin{array}{rr}1&1\\1&-1\end{array}\rightp \begin{pmatrix} 1&0\\0&\lambda_j \end{pmatrix} \frac{1}{\sqrt2}\leftp\begin{array}{rr}1&1\\1&-1\end{array}\rightp \ket{\eta} = \frac{1}{2} \begin{pmatrix} 1+\lambda_j&1-\lambda_j\\1-\lambda_j&1+\lambda_j \end{pmatrix} \ket{\eta}.$

Поэтому

$\displaystyle \Xi(U) =\sum\limits_{j}^{} \overbrace{\frac{1}{2} \begin{pmatrix} 1+\lambda_j&1-\lambda_j\\1-\lambda_j&1+\lambda_j \end{pmatrix} }^{R_j} \otimes\Pi_{\calL_j}.$

Теперь подсчитаем условные вероятности. Собственные числа унитарного оператора равны по модулю 1, поэтому можно полагать $\lambda_j= e^{2\pi\ii \varphi_j}$ . В результате имеем

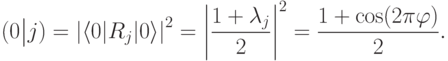
$\PP(0\big| j)=\left|\langle 0|R_j|0\rangle \right|^2= \left|\frac{1+\lambda_j}{2}\right|^2=\frac{1+\cos(2\pi\varphi)}{2}.$

В дальнейшем именно с помощью такого оператора мы будем оценивать собственные числа. Для этого придется брать разные биты в качестве первых сомножителей (разные "приборы"). Конечно, следует убедиться, что это корректно (т.е., что вероятности будут перемножаться).

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Измеряющие операторы

Вопросы и ответы