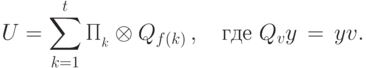Измеряющие операторы
Свойства измеряющих операторов.
Мы будем рассматривать измеряющие операторы, соответствующие одному и тому же ортогональному разложению  .
.
1. Произведение измеряющих операторов — измеряющий оператор. Действительно, пусть есть два измеряющих оператора
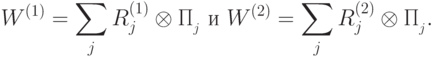
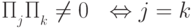 , имеем
, имеем
2. Условные вероятности для произведения измеряющих "разными приборами" операторов перемножаются. Более точно, пусть  , а
, а 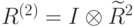 . Тогда
. Тогда  . Это равенство следует непосредственно из определения условных вероятностей и из очевидного тождества
. Это равенство следует непосредственно из определения условных вероятностей и из очевидного тождества
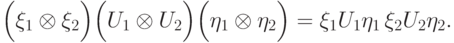
3. Формула полной вероятности. Пусть есть измеряющий оператор  . Если применить его к состоянию
. Если применить его к состоянию  , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде:
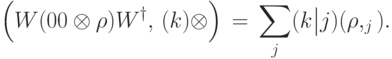
Доказательство. 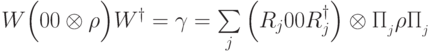 . Ранее было доказано, что
. Ранее было доказано, что  . Далее,
. Далее,
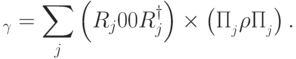
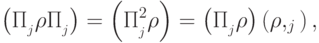
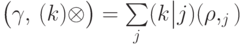 .
.Задача 11.1. Докажите формулу полной вероятности напрямую, не используя взятия частичного следа.
Задача 11.2. "Обратимое измерение" Пусть  — измеряющий оператор,
— измеряющий оператор, 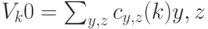 . (Имеется в виду, что операторы
. (Имеется в виду, что операторы  действуют на
действуют на  q-бит; первые
q-бит; первые  q-бит (т.е.
q-бит (т.е.  ) — "полезный результат", остальные
) — "полезный результат", остальные  q-бит (т.е.
q-бит (т.е.  ) — "мусор".) Допустим, что
) — "мусор".) Допустим, что  измеряет некоторую функцию
измеряет некоторую функцию 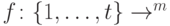 с вероятностью ошибки
с вероятностью ошибки 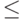 , т.е.
, т.е.

 и
и 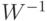 квантовую схему полиномиального размера, реализующую с точностью
квантовую схему полиномиального размера, реализующую с точностью 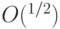 новый измеряющий оператор
новый измеряющий оператор