Определение квантового вычисления. Примеры
Квантовый поиск: алгоритм Гровера.
Итак, мы имеем определение квантового вычисления. Теперь можно заняться сравнением эффективности классического и квантового вычисления. Во введении упоминались три основных примера, для которых квантовое вычисление оказывается, по-видимому, эффективнее классического. Мы начнем с того из них, в котором квантовое вычисление заведомо эффективнее (хотя ускорение лишь "полиномиальное").
Дадим определение универсальной переборной задачи в классической и квантовой постановке.
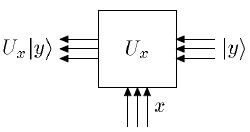
Пусть имеется устройство (см. рисунок), которое по входам  и
и  определяет значение некоторого предиката
определяет значение некоторого предиката 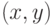 . Нас интересует предикат
. Нас интересует предикат  . Это похоже на определение класса NP, но сейчас нам недоступна внутренняя структура устройства, вычисляющего предикат
. Это похоже на определение класса NP, но сейчас нам недоступна внутренняя структура устройства, вычисляющего предикат  . В таких условиях на классическом компьютере значение предиката
. В таких условиях на классическом компьютере значение предиката 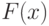 нельзя вычислить быстрее, чем за
нельзя вычислить быстрее, чем за  шагов, где
шагов, где  — количество битов в записи
— количество битов в записи  .
.
Оказывается, что на квантовом компьютере можно вычислить значение предиката 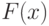 и даже найти
и даже найти  , на котором выполнено
, на котором выполнено 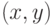 , за время
, за время  . Получены также и нижние оценки, показывающие, что в этой постановке квантовые устройства дают лишь полиномиальное ускорение по сравнению с классическими.
. Получены также и нижние оценки, показывающие, что в этой постановке квантовые устройства дают лишь полиномиальное ускорение по сравнению с классическими.
В квантовой постановке задача выглядит так. Вход  по-прежнему классический, но сам "черный ящик" — квантовое устройство, и вход
по-прежнему классический, но сам "черный ящик" — квантовое устройство, и вход  (варианты ответа) мы будем считать квантовым. Поэтому наш оракул (или "черный ящик") задает оператор
(варианты ответа) мы будем считать квантовым. Поэтому наш оракул (или "черный ящик") задает оператор 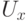 , действующий по правилу
, действующий по правилу
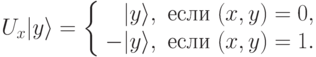
Нужно вычислить значение 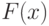 и найти "ответ"
и найти "ответ"  (при котором выполнен
(при котором выполнен 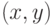 ).
).
Результаты, о которых уже упоминалось, формулируются так (см.[31, 48]): существуют две константы 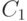 и
и 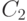 такие, что есть схема размера
такие, что есть схема размера 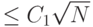 , решающая задачу для любого предиката
, решающая задачу для любого предиката 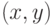 ; а для любой схемы размера
; а для любой схемы размера  существует предикат
существует предикат 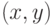 , при котором задача не решается на этой схеме (т.е. схема дает неправильный ответ с вероятностью
, при котором задача не решается на этой схеме (т.е. схема дает неправильный ответ с вероятностью 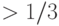 ).
).
Мы разберем упрощенную постановку: считаем, что "ответ" существует и единствен, обозначим его через  ; нужно найти
; нужно найти  . Схема, которую мы для этого построим, будет примером "прямого" квантового вычисления; она будет описана в терминах преобразований базисных векторов.
. Схема, которую мы для этого построим, будет примером "прямого" квантового вычисления; она будет описана в терминах преобразований базисных векторов.
Рассмотрим два оператора:

и
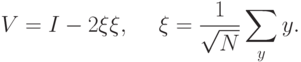
Оператор  в матричной форме может быть записан так (напомним, что
в матричной форме может быть записан так (напомним, что  ):
):
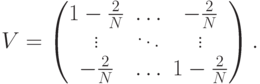
Оператор  нам задан (это оракул). Построим квантовую схему, вычисляющую
нам задан (это оракул). Построим квантовую схему, вычисляющую  . Действовать будем так: переведем
. Действовать будем так: переведем 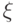 в
в 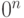 некоторым оператором
некоторым оператором  , затем применим оператор
, затем применим оператор  , после чего применим
, после чего применим 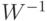 .
.
Построить оператор  , который переводит
, который переводит 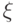 в
в 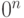 , просто. Это
, просто. Это  , где оператор
, где оператор  — из стандартного базиса (см.
"Базисы для квантовых схем"
). Действительно,
— из стандартного базиса (см.
"Базисы для квантовых схем"
). Действительно, 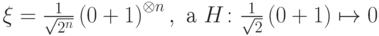 .
.
Теперь построим реализацию оператора  . Используем обратимую классическую схему, реализующую оператор
. Используем обратимую классическую схему, реализующую оператор 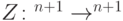 ,
,
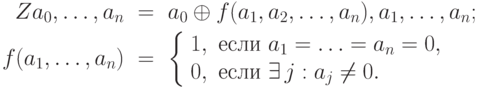
 .) Поскольку
.) Поскольку  имеет малую схемную сложность (в классическом смысле), по лемме для вычисления
имеет малую схемную сложность (в классическом смысле), по лемме для вычисления  существует небольшая схема (в которой берутся "напрокат" дополнительные q-биты).
существует небольшая схема (в которой берутся "напрокат" дополнительные q-биты).Схема, реализующая оператор  , изображена на рис. рис. 8.1.. Центральная часть, включающая в себя
, изображена на рис. рис. 8.1.. Центральная часть, включающая в себя  ,
,  и
и  , реализует оператор
, реализует оператор  . В схеме используется оператор
. В схеме используется оператор  (
(  из стандартного базиса).
из стандартного базиса).
Заметим, что  и
и  действуют тождественно на векторах с нулевыми значениями q-битов, взятых напрокат. Поэтому решающую роль играет оператор
действуют тождественно на векторах с нулевыми значениями q-битов, взятых напрокат. Поэтому решающую роль играет оператор  , действующий на вспомогательный q-бит, который также не меняется после всего вычисления.
, действующий на вспомогательный q-бит, который также не меняется после всего вычисления.
Пусть вас не смущает то, что  действует только на "управляемый" q-бит, а меняется в результате весь вектор. Вообще, различие между "чтением" и "записью" в квантовом случае неабсолютно и зависит от выбора базиса. Приведем соответствующий пример.
действует только на "управляемый" q-бит, а меняется в результате весь вектор. Вообще, различие между "чтением" и "записью" в квантовом случае неабсолютно и зависит от выбора базиса. Приведем соответствующий пример.
Напишем матрицу  в базисе
в базисе 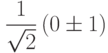 для каждого из q-бит. Другими словами, запишем матрицу для оператора
для каждого из q-бит. Другими словами, запишем матрицу для оператора 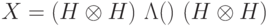 . Схема для этого оператора изображена на рис. рис. 8.2. Используя равенство
. Схема для этого оператора изображена на рис. рис. 8.2. Используя равенство  , найдем действие
, найдем действие  на базисном векторе:
на базисном векторе:
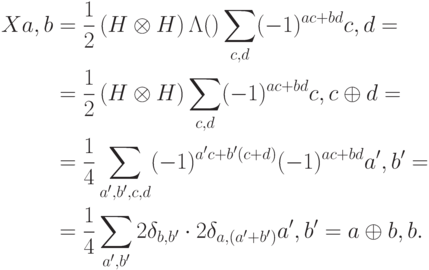
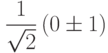
Задача 8.2. Что будет, если изменить базис только в одном бите? Например, как будет выглядеть матрица оператора, схема которого изображена на рисунке? Попробуйте также поменять базис в другом бите.
Вернемся к построению схемы для универсальной переборной задачи. Оракул  нам задан, и мы реализовали оператор
нам задан, и мы реализовали оператор 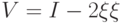 . Из вектора
. Из вектора 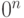 можно получить вектор
можно получить вектор 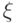 применением оператора
применением оператора  (
(  ). Теперь с помощью операторов
). Теперь с помощью операторов  и
и  построим из вектора
построим из вектора 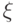 искомый вектор
искомый вектор  . Для этого будем поочередно действовать операторами
. Для этого будем поочередно действовать операторами 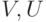 :
:
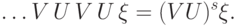
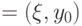 инвариантно относительно обоих операторов, а, значит, и относительно
инвариантно относительно обоих операторов, а, значит, и относительно 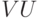 . Поскольку вектор
. Поскольку вектор 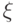 принадлежит этому подпространству, достаточно рассмотреть действие
принадлежит этому подпространству, достаточно рассмотреть действие 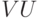 на нем.
на нем.Композиция двух отражений относительно двух прямых есть поворот на удвоенный угол между этими прямыми. Угол легко вычислить, 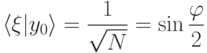 , т.е. эти прямые почти перпендикулярны. Поэтому можно написать
, т.е. эти прямые почти перпендикулярны. Поэтому можно написать 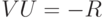 , где
, где  — поворот на малый угол
— поворот на малый угол  . Но тогда
. Но тогда  , где
, где 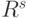 — поворот на угол
— поворот на угол 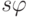 . Знак нас не интересует (фазовые множители не меняют вероятностей). При больших
. Знак нас не интересует (фазовые множители не меняют вероятностей). При больших  имеем
имеем 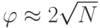 . Тогда после
. Тогда после  итераций исходный вектор повернется на угол
итераций исходный вектор повернется на угол 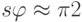 и станет близок к искомому вектору. Это и означает, что система окажется в состоянии
и станет близок к искомому вектору. Это и означает, что система окажется в состоянии  с вероятностью, близкой к единице.
с вероятностью, близкой к единице.
Если решается переборная задача в общей постановке (т.е. ответов может быть несколько, а может не быть вообще), требуются дополнительные технические ухищрения. Число шагов для поворота от исходного вектора к какому-нибудь вектору из подпространства, порожденного векторами ответов, обратно пропорционально корню из числа решений.