НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 8: Определение квантового вычисления. Примеры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 611 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Универсальная квантовая схема.

Второй из примеров, упомянутых во введении, — моделирование квантовомеханических систем. Это нечетко поставленная задача, так как большую роль в ней играет выбор конкретной системы и выделение существенных "степеней" свободы. С математической точки зрения, более корректно говорить о моделировании квантовых схем.

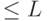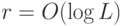Квантовые схемы имеют конструктивное описание, если указать точность, с которой известны матричные элементы операторов, входящих в схему. Пусть есть описание квантовой схемы , размера $\leq L$ и точности $\delta$ . Элементами этой схемы могут быть любые унитарные операторы на $r=O(\log L)$ q-битах (так чтобы полная длина описания схемы не превышала $\poly(L,\log(1/\delta))\$ ,). Обозначим оператор, реализуемый этой схемой, через Op(Z) .

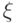Из результатов задач 7.1 и 7.11 следует, что можно построить универсальную квантовую схему размера $\poly(L, \log 1/\delta)$ , которая моделирует работу произвольной квантовой схемы следующим образом. Если задано описание некоторой схемы Op(Z) размера и ее вход $\ket\xi$ , то

$\Bigl\| U(\ket{Z}\otimes\ket\xi)-\ket{Z}\otimes Op(Z)\ket\xi\Bigr\|= O(L\delta).$

Квантовые алгоритмы и класс BQP.

До сих пор мы рассматривали неоднородные вычисления (вычислялись булевы функции). Алгоритмы вычисляют функции на словах произвольной длины. Определение квантового алгоритма можно дать, используя уже введенные квантовые схемы. Пусть есть функция 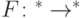$F\colon{} \cb^*\to \cb^*$ , длина результата — полином от длины входа. Ей сопоставляется последовательность булевых функций (ограничения на входы длины ) 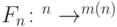$F_n\colon{} \cb^n\to \cb^{m(n)}$ . Квантовый алгоритм для вычисления — это однородная последовательность схем, вычисляющих F_n . 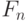"Однородная" означает, что по можно построить описание соответствующей схемы на обычной полиномиально ограниченной машине Тьюринга. 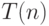Будем говорить, что алгоритм работает за время T(n) , если размер схемы, вычисляющей 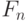F_n , равен T(n) .

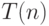Замечание 8.1. Можно определить квантовую машину Тьюринга и непосредственно через суперпозиции различных состояний ленты МТ (первоначальное определение Д.Дойча было именно таким). Наше определение оказывается эквивалентным.

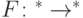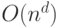Определение 8.2. Функция $F\colon\cb^*\to\cb^*$ принадлежит классу $\BQP$ , если есть квантовый алгоритм ее вычисления, работающий за время O(n^d) для некоторой константы .

Как соотносится класс BQP{} с сложностными классами, введенными ранее?

Задача 8.3. Докажите, что

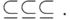
$\BPP\subseteq \BQP\subseteq \PPP \subseteq \PSPACE.$

Класс $\PPP$ состоит из предикатов вида

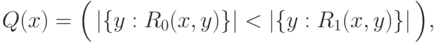
$Q(x)=\Bigl(\, |\{y:R_0(x,y)\}| < |\{y:R_1(x,y)\}| \,\Bigr),$

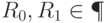где $R_0,R_1\in\P$ , и учитываются только

с длиной меньше некоторого полинома q(x)

.

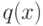Это почти все, что известно о соотношениях между BQP и другими сложностными классами. Косвенное свидетельство в пользу строгого включения $\BPP\subset\BQP$ дает существование эффективных квантовых алгоритмов для некоторых теоретико-числовых задач, традиционно считаемых трудными (см. раздел 12).

Заметим также, что в последнее время появились интересные результаты о квантовых аналогах некоторых более сильных сложностных классов (не описанных в части I).

Задача 8.4. Постройте квантовые схемы полиномиального размера в базисе из операторов на двух q-битах, которые выполняют следующие действия:

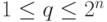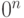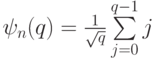для заданного числа , $1\leq q\leq 2^n$ , записанного двоичными цифрами, преобразовать состояние $\ket{0^n}$ в состояние $\ket{\psi_n(q)}=\frac{1}{\sqrt{q}}\sum\limits_{j=0}^{q-1}\ket{j}$ ;
преобразовать 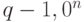$\ket{q-1,0^n}$ в $\ket{q-1}\otimes\ket{\psi_n(q)}$ , считая, что записано двоичными цифрами;
выполнить преобразование Фурье на группе 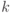$\ZZ_k$ при :
$\[ U_k\ket{x}=\frac{1}{\sqrt{k}}\, \sum_{y=0}^{k-1} \exp\left(2\pi\ii\frac{xy}{k}\right) \ket{y},$
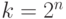считая, что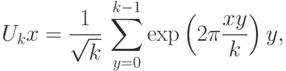 и записаны двоичными цифрами; (в этом случае найдите схему размера 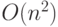).