Московский государственный университет имени М.В.Ломоносова
Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 613 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00
Специальности: Программист
Теги:
Дополнительный материал 1:
Решения задач
Из раздела 9
9.1. Пусть 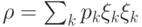 . Проверим условия 1)—3) для
. Проверим условия 1)—3) для  .
.
Условие 1): очевидно.
Условие 2):  .
.
Условие 3):  .
.
И наоборот, если  удовлетворяет 1)—3), то
удовлетворяет 1)—3), то 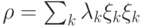 , где
, где 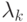 — собственные числа, а
— собственные числа, а 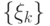 — ортонормированный базис из собственных векторов.
— ортонормированный базис из собственных векторов.
9.2 Вектору  можно естественным образом сопоставить оператор
можно естественным образом сопоставить оператор 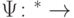 . Пусть
. Пусть 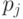 — ненулевые собственные числа оператора
— ненулевые собственные числа оператора

 является матрицей плотности,
является матрицей плотности, 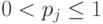 . Положим
. Положим 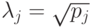 , а в качестве множества
, а в качестве множества 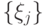 возьмем любую ортонормированную систему собственных векторов, соответствующих собственным числам
возьмем любую ортонормированную систему собственных векторов, соответствующих собственным числам 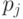 .
.Оператор  можно представить в виде
можно представить в виде
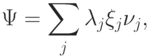
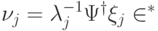 . Соответственно,
. Соответственно, 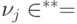 . Переобозначив
. Переобозначив 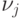 через
через 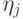 , получаем искомое разложение Шмидта.
, получаем искомое разложение Шмидта.9.3 Условие  , как следует из решения предыдущей задачи, позволяет выбрать разложения Шмидта для
, как следует из решения предыдущей задачи, позволяет выбрать разложения Шмидта для 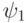 и
и 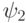 с одинаковыми
с одинаковыми 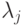 и
и 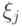 . Запишем эти разложения
. Запишем эти разложения
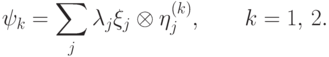
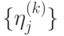 — ортонормированные семейства, существует унитарный оператор
— ортонормированные семейства, существует унитарный оператор  , такой что
, такой что 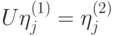 для всех
для всех  . Тогда
. Тогда