|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Матричные игры и линейные программы как модели поведения
Двойственные задачи линейного программирования и рыночное равновесие
Рассмотрим задачу линейного программирования с ограничениями вида
неравенств в следующей интерпретации1Многие другие интерпретации
задач линейного программирования представлены, например, в известной
книге: Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория,
методы и приложения. М.: Наука, 1969.. Пусть некоторая фирма P1
располагает m видами сырья, используя которые, она может
выпускать n
типов продукции. Известны цены  ,
, 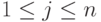 ,
по которым происходит реализация единицы продукции каждого j -го типа, составляющие вектор-столбец
,
по которым происходит реализация единицы продукции каждого j -го типа, составляющие вектор-столбец

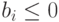 ,
,  , сырья
каждого вида, составляющие вектор-столбец
, сырья
каждого вида, составляющие вектор-столбец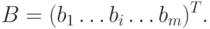
 ,
, 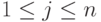 ,
характеризующих количество сырья вида i, необходимое для
производства единицы продукции типа j. Требуется определить плановые
уровни wj,
,
характеризующих количество сырья вида i, необходимое для
производства единицы продукции типа j. Требуется определить плановые
уровни wj, 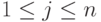 , производства продукции
каждого типа, обеспечивающие максимальный доход
при заданных сырьевых ресурсах.
, производства продукции
каждого типа, обеспечивающие максимальный доход
при заданных сырьевых ресурсах.Если принять, что план производства описывается вектором-столбцом
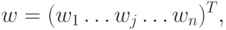
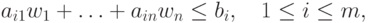
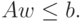
Теперь поставленная задача выбора плана 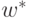 ,
максимизирующего доход
,
максимизирующего доход
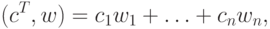
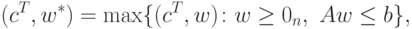 |
( 12.1) |
Заметим, что указанный в (12.1)
вектор-столбец 0n соответствует началу координат
в пространстве Rn, а условие  эквивалентно
координатным
неравенствам
эквивалентно
координатным
неравенствам  ,
, 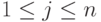 . В дальнейшем
(там, где это не может вызвать сомнений) мы будем (для краткости записи) опускать
нижний индекс при 0n, указывающий размерность пространства.
. В дальнейшем
(там, где это не может вызвать сомнений) мы будем (для краткости записи) опускать
нижний индекс при 0n, указывающий размерность пространства.
Примем, что фирма P1, помимо продажи своей продукции, может также продавать имеющиеся у нее запасы сырья по ценам, характеризуемым вектором-столбцом
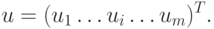
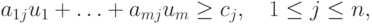
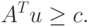
Рынок, с которым взаимодействует фирма P1, продавая продукцию (или сырье), будем рассматривать как вторую (агрегированную) сторону в описываемой операции и обозначать P2. Естественно принять, что участники рынка, покупающие сырье, заинтересованы в уменьшении своих затрат. Поэтому их задачу можно описать как формирование вектора цен u*, удовлетворяющего условиям
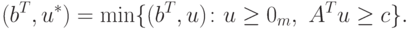 |
( 12.2) |
Для двойственной пары задач (12.1), (12.2) линейного программирования справедлива теорема двойственности . 2Два разных доказательства этой теоремы содержатся в учебном пособии: Мухачева Э.А. Рубинштейн Г.Ш. Математическое программирование. Новосибирск: Наука, 1987. См. также: Васильев Ф.П., Иваницкий А.Ю. Линейное программирование. М.: Факториал, 1998. Согласно этой теореме, если одна из задач (12.1) и (12.2) имеет решение, то и вторая задача имеет решение, причем в этом случае
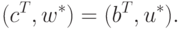 |
( 12.3) |
Величины, введенные при описании пары двойственных задач (12.1), (12.2), собраны (для наглядности) ниже.
Заметим, что фактически мы рассматриваем разные механизмы, определяющие цены на продукцию и цены на сырье. Цены, по которым реализуется продукция, считаются заданными и не зависящими от объемов производства. Такая ситуация возможна, например, в случае, когда существует внешний механизм регулирования этих цен, призванный стимулировать производство и продажу товаров из рассматриваемого перечня. При этом цены на сырье (зависящие согласно (12.2) от заданных цен на продукцию) формируются как результат описанных выше взаимодействий производителя и рынка.
Примем теперь, что производитель, выбрав некоторый план производства  , может продавать на рынке не только произведенную
продукцию, но и остатки сырья. Кроме того, он может закупать на рынке недостающее
сырье. Продажа и закупка сырья происходит по одним и тем же ценам
, может продавать на рынке не только произведенную
продукцию, но и остатки сырья. Кроме того, он может закупать на рынке недостающее
сырье. Продажа и закупка сырья происходит по одним и тем же ценам 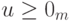 , которые формирует рынок. В такой постановке доход
производителя, который мы будем рассматривать как критерий M(w,u)
первой стороны, определяется выражением
, которые формирует рынок. В такой постановке доход
производителя, который мы будем рассматривать как критерий M(w,u)
первой стороны, определяется выражением
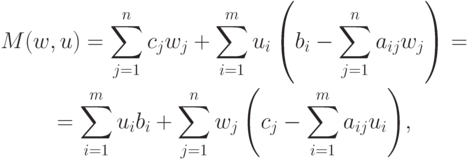 |
( 12.4) |
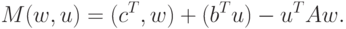 |
( 12.5) |
 является допустимым. Допустим
также и любой вектор
является допустимым. Допустим
также и любой вектор 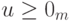 , формируемый рынком, интересы
которого противоположны интересам производителя,
желающего максимизировать свой доход.
, формируемый рынком, интересы
которого противоположны интересам производителя,
желающего максимизировать свой доход.В результате получаем, что отношения сторон P1 и P2 характеризуются антагонистической игрой с ядром M(w,u)
и множествами стратегий сторон, определяемыми соответственно
условиями  и
и 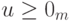 .
.
Исследуем вопрос о существовании равновесного поведения сторон, т.е.
вопрос о существовании пары стратегий (w*,u*), являющейся
седловой точкой ядра M(w,u). Оценим величину дохода
производителя, гарантируемую выбором плана  .
Согласно (12.4),
.
Согласно (12.4),
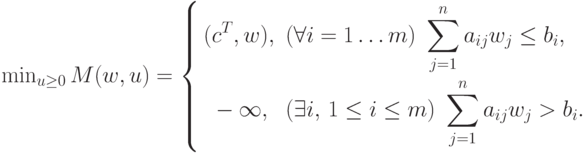
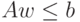 выбор
вектора u=0m минимизирует доход M(w,u),
поскольку вынуждает производителя отдавать излишки сырья по нулевым ценам.
В случае, когда реализация принятого производителем плана
выбор
вектора u=0m минимизирует доход M(w,u),
поскольку вынуждает производителя отдавать излишки сырья по нулевым ценам.
В случае, когда реализация принятого производителем плана  требует покупки недостающего сырья вида i, вторая сторона может
неограниченно уменьшать доход P1 путем увеличения цены ui
на дефицитное (для P1 ) i -е сырье. Следовательно,
требует покупки недостающего сырья вида i, вторая сторона может
неограниченно уменьшать доход P1 путем увеличения цены ui
на дефицитное (для P1 ) i -е сырье. Следовательно,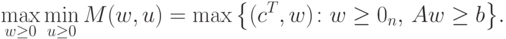 |
( 12.6) |
Теперь оценим возможные максимальные затраты второй
стороны P2, соответствующие некоторому вектору 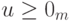 цен за сырье. Согласно (12.4),
цен за сырье. Согласно (12.4),
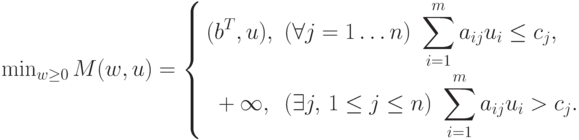
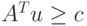 выбор плана w=0n (т.е. отказ от производства продукции)
максимизирует доход M(w,u) первой стороны (или затраты
второй стороны). В этом случае продажа сырья дает не меньший доход, чем
продажа продукции, произведенной из этого сырья.
выбор плана w=0n (т.е. отказ от производства продукции)
максимизирует доход M(w,u) первой стороны (или затраты
второй стороны). В этом случае продажа сырья дает не меньший доход, чем
продажа продукции, произведенной из этого сырья.Допустим, что доход от продажи продукции некоторого типа j превышает затраты на приобретение сырья, необходимого для производства единицы этой продукции. Тогда производитель может неограниченно увеличивать свой доход, закупая сырье в ассортименте, необходимом для производства продукции типа j. Заметим, что это рассуждение предполагает наличие у производителя необходимых оборотных средств (или возможность использования кредитов). Таким образом (при указанных условиях),
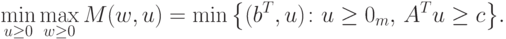 |
( 12.7) |
Теперь из (12.1)-(12.3) вытекает, что

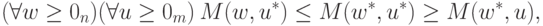 |
( 12.8) |
 |
( 12.9) |

