|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Нижегородский государственный университет им. Н.И.Лобачевского
Опубликован: 26.04.2007 | Доступ: свободный | Студентов: 1445 / 138 | Оценка: 3.69 / 3.54 | Длительность: 14:45:00
ISBN: 978-5-9556-0072-7
Тема: Математика
Специальности: Математик
Лекция 6:
Об устойчивости баланса спроса и предложения
Мотивация поведения спекулянта
Согласно (5.6) и (5.10), прибыль, получаемая спекулянтом в результате каждой описанной выше операции купли-продажи, составляет величину
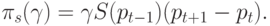 |
( 5.23) |
 |
( 5.24) |
 и
и  из (5.2) и (5.15).
из (5.2) и (5.15).Действительно, из (5.8) выводим, что
![p_{t+1}=p_{\max}-[S(p_t)+\gamma S(p_{t-1})]/A.](/sites/default/files/tex_cache/76c0ff82fe48522b4d431a21c69af4b8.png)
![p_{t+1}-p_t=[B(p_{t-1}-p_t)-2\gamma S(p_{t-1})]/A.](/sites/default/files/tex_cache/d871da177c60ca3540e2c6c69f68e272.png)
![p_{t+1}-p_t=[\lambda (S(p_{t-1})-D(p_{t-1}))-\gamma (\lambda +2)S(p_{t-1})]/A.](/sites/default/files/tex_cache/78f2e9f461ffe716d99cde639804d27f.png)
 из (5.15),
окончательно выводим, что
из (5.15),
окончательно выводим, что![\pi_s(\gamma)=\gamma S^2(p_{t-1})[\lambda \theta-\gamma(\lambda+2)]/A.](/sites/default/files/tex_cache/944ba59225ad9be8a4f302a15e55dc96.png)
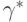 как решение уравнения
как решение уравнения![\frac{d\pi_s(\gamma)}{d\gamma}=S^2(p_{t-1})[\lambda
\theta-2\gamma(\lambda+2)]/A=0.](/sites/default/files/tex_cache/6fa5db1cc8a29ee3ce91604bedf28d2b.png)
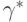 из (5.24).
При этом вторая производная от
из (5.24).
При этом вторая производная от 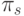 по
по  отрицательна в точке
отрицательна в точке 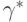 .
.Непосредственной проверкой можно установить, что значение коэффициента 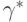 из (5.24) принадлежит интервалу
из (5.24) принадлежит интервалу 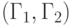 из (5.13),
если величина
из (5.13),
если величина  из (5.2) удовлетворяет условиям
из (5.2) удовлетворяет условиям
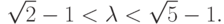
Отметим, что точке равновесия по Штакельбергу, обнаруженной в
рассмотренном выше примере, соответствует единичное значение  ,
поскольку для всех точек кривой (4.29), на которой находится точка
равновесия (4.29),
справедливо равенство A=B ; ср. (4.9) и (4.22).
Следовательно, равновесная цена
,
поскольку для всех точек кривой (4.29), на которой находится точка
равновесия (4.29),
справедливо равенство A=B ; ср. (4.9) и (4.22).
Следовательно, равновесная цена
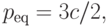 |
( 5.24) |
