Кольцо многочленов от одной переменной
Упражнение 1.13.34. Наибольший общий делитель d(x) многочленов f(x) = 3x5-4x4+x3-3x2+4x-1 и g(x) = 3x5+5x4+x3-x2-3x+1 представить в виде d(x)=f(x)u(x)+g(x)v(x), где u(x), v(x) - многочлены степеней, меньших чем степени многочленов g(x) и f(x) соответственно.
Решение. Сначала с помощью алгоритма Евклида находим d(x)=3x3+2x2+2x-1, при этом
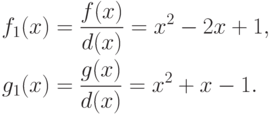
Ищем многочлены u(x) и v(x) такие, что 1=f1(x)u(x)+g1(x)v(x).
Так как степени многочленов u(x) и v(x) должны быть меньше двух, то u(x)=ax+b, v(x)=cx+d, где 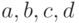 . Приравнивая в коэффициенты при одинаковых степенях переменной x, получаем систему линейных уравнений для a, b, c, d. Решая эту систему, получаем, что a=3, b=5, c=-3, d=4. Итак, d(x)=3x3+2x2+2x-1=f(x)(3x+5)+g(x)(-3x+4).
. Приравнивая в коэффициенты при одинаковых степенях переменной x, получаем систему линейных уравнений для a, b, c, d. Решая эту систему, получаем, что a=3, b=5, c=-3, d=4. Итак, d(x)=3x3+2x2+2x-1=f(x)(3x+5)+g(x)(-3x+4).
Определение 1.13.35. Пусть K - поле, ![f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\in K[x],\quad a_n,...,a_0\in K](/sites/default/files/tex_cache/6b3833fa4c6b885fef30c57adf85fc94.png) . Если
. Если 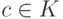 , то элемент
, то элемент  назовем значением многочлена f(x) при x=c. Таким образом, получаем отображения:
назовем значением многочлена f(x) при x=c. Таким образом, получаем отображения: 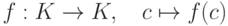 (полиномиальная функция, определяемая многочленом f(x) );
(полиномиальная функция, определяемая многочленом f(x) ); ![K[x]\to K,\quad f(x)\mapsto f(c)](/sites/default/files/tex_cache/88cf38215d9a5fd0d6d8220bd37d0b95.png) (ясно, что если f(x)=g(x) в K[x], то f(c)=g(c) для всех
(ясно, что если f(x)=g(x) в K[x], то f(c)=g(c) для всех 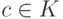 ).
).
Лемма 1.13.36. Если в K[x] 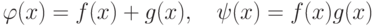 и
и 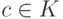 , то
, то 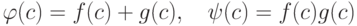 . Таким образом, отображение
. Таким образом, отображение ![\Delta_c: K[x]\to K,\quad f(x)\mapsto f(c)](/sites/default/files/tex_cache/15f7de6c8b8c3ce5b9f468f441df95b6.png) , является гомоморфизмом колец (при этом
, является гомоморфизмом колец (при этом ![\text{Ker}\Delta_c=\{f(x)\in K[x] \mid\allowbreak f(c)=0\}](/sites/default/files/tex_cache/2d45a7046ed9d86f81278913975fa67d.png) ).
).
Доказательство следует из определения сложения и умножения многочленов в кольце K[x].
Определение 1.13.37. Элемент 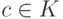 называется корнем многочлена
называется корнем многочлена ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) , если f(c)=0 .
, если f(c)=0 .
Теорема 1.13.38 (Безу). Пусть 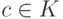 . Остаток от деления многочлена f(x) в кольце K[x] на множитель x-c равен значению f(c) многочлена f(x) при x=c.
. Остаток от деления многочлена f(x) в кольце K[x] на множитель x-c равен значению f(c) многочлена f(x) при x=c.
Доказательство. В силу алгоритма деления f(x)=(x-c)q(x)+r(x), где или r(x)=0, или 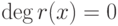 , и поэтому
, и поэтому 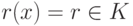 . Итак, f(x)=(x-c)q(x)+r, следовательно, f(c)=(c-c)q(c)+r=r, и поэтому f(x)=(x-c)q(x)+f(c).
. Итак, f(x)=(x-c)q(x)+r, следовательно, f(c)=(c-c)q(c)+r=r, и поэтому f(x)=(x-c)q(x)+f(c).
Следствие 1.13.39. Элемент 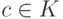 является корнем многочлена
является корнем многочлена ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) тогда и только тогда, когда многочлен f(x) делится на x-c.
тогда и только тогда, когда многочлен f(x) делится на x-c.
Замечание 1.13.40.
- Если
 ,
, 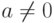 , то делимость многочлена
, то делимость многочлена ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) на многочлен
на многочлен 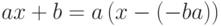 равносильна делимости на многочлен x-c,
равносильна делимости на многочлен x-c, 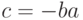 , и поэтому нахождение корней многочлена
, и поэтому нахождение корней многочлена ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) в поле K равносильно нахождению его линейных делителей в кольце K[x].
в поле K равносильно нахождению его линейных делителей в кольце K[x]. - Если
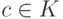 ,
, ![\Delta_c: K[x]\to K](/sites/default/files/tex_cache/7f5952626741f5f3af02c5bf9363d424.png) ,
,  , то
, то ![\text{Ker}\Delta_c=\{f(x)\in K[x]\mid f(c)=0\}= (x-c)K[x]=I_c](/sites/default/files/tex_cache/2028f719fab27bdc9d2d60bd60d0f4a7.png) (главный идеал в кольце K[x], порожденный многочленом x-c ).
(главный идеал в кольце K[x], порожденный многочленом x-c ).
Замечание 1.13.41 (схема (алгоритм) Горнера деления многочлена ![\boldsymbol{f(x)\in K[x]}](/sites/default/files/tex_cache/bc3ffab7de538549367ecd797a57866d.png) на линейный многочлен
на линейный многочлен  ,
, 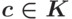 )
)
Пусть ![f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\in K[x]](/sites/default/files/tex_cache/7e5b8bf038c6fcb7af0498e1b70f4517.png) ,
,
![\begin{gathe}
f(x)=(x-c)q(x)+r,\quad r\in K,
\\
q(x)=b_{n-1}x^{n-1}+...+b_1x+b_0\in K[x].
\end{gathe}](/sites/default/files/tex_cache/8a97f5dae50cc9a79de1467c6c1c73e9.png)
Тогда, приравнивая коэффициенты при xn,xn-1,...,x,1, соответственно получаем
![\begin{align*} & a_n = b_{n-1};
\\ & a_{n-1}=b_{n-2}-cb_{n-1};
\\ & a_{n-2}=b_{n-3}-cb_{n-2};
\\[-1pt] & ...
\\[-1pt] & a_k = b_{k-1}-cb_k;
\\[-1pt] & ...
\\[-1pt] & a_1=b_0-cb_1;
\\ & a_0=r-cb_0.
\end{align*}](/sites/default/files/tex_cache/729448def50aa1f141c428caf4984333.png)
Пересчитывая, получаем
![\begin{align*} & b_{n-1}=a_n;
\\ & b_{n-2}=cb_{n-1}+a_{n-1};
\\ & b_{n-3}=cb_{n-2}+a_{n-2};
\\[-1pt] & ...
\\[-1pt] & b_{k-1}=cb_k+a_k;
\\[-1pt] & ...
\\[-1pt] & b_0=cb_1+a_1;
\\ & r=cb_0+a_0.
\end{align*}](/sites/default/files/tex_cache/85069b9d5d2bf72a765bb7f29100c763.png)
Таким образом, коэффициенты частного bn-1,...,b1,b0 и остаток r=f(c) последовательно вычисляются по коэффициентам an,...,a1,a0 и элементу c, если использовать однотипную процедуру
Пример 1.13.42. Пусть f(x)=2x4-x2+3x-2, c=-2. Тогда
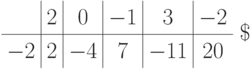
поэтому f(x)=(x+2)q(x)+20, где q(x)=(x+2)(2x3-4x2+7x-11).
Замечание 1.13.43.
- Схема Горнера дает быстрый алгоритм вычисления значения r=f(c) многочлена
![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) в точке c (минимизируя число умножений).
в точке c (минимизируя число умножений). - Последовательное применение схемы Горнера позволяет построить эффективный алгоритм записи многочлена f(x) в виде формулы Тейлора по степеням (x-c). А именно, при первом применении схемы Горнера крайний правый коэффициент равен f(c), при втором применении крайний справа коэффициент равен f'(c), при третьем -
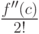 , и так далее. Таким образом, если
, и так далее. Таким образом, если 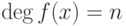 , то
, то 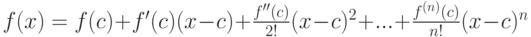 (формула Тейлора).
(формула Тейлора).
Например, для f(x)=x4-6x3-2x2+5x-4 и c=5 имеем
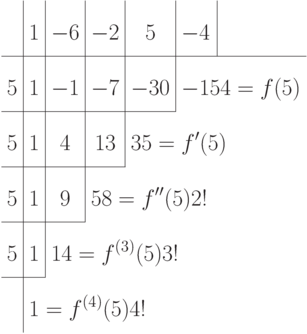
Таким образом, f(x)=(x-5)4+14(x-5)3+58(x-5)2+35(x-5)-154.
Определение 1.13.44.Пусть ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) ,
, 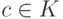 , и c - корень многочлена f(x), т. е. f(c)=0. По теореме Безу многочлен f(x) делится на x-c. Возможно, многочлен f(x) делится на более высокие степени многочлена x-c. Пусть
, и c - корень многочлена f(x), т. е. f(c)=0. По теореме Безу многочлен f(x) делится на x-c. Возможно, многочлен f(x) делится на более высокие степени многочлена x-c. Пусть 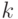 - такое натуральное число, что f(x) делится на (x-c)k, но не делится на (x-c)k+1, поэтому
- такое натуральное число, что f(x) делится на (x-c)k, но не делится на (x-c)k+1, поэтому 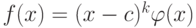 , многочлен
, многочлен ![\varphi(x)\in K[x]](/sites/default/files/tex_cache/86377a019026b7835278d8e24aa2e1cd.png) уже не делится на x-c (это равносильно тому, что
уже не делится на x-c (это равносильно тому, что  ). В этом случае число k назовем кратностью корня c многочлена f(x), а сам корень c - k -кратным корнем многочлена f(x). Если k=1, то корень c называется простым корнем многочлена f(x).
). В этом случае число k назовем кратностью корня c многочлена f(x), а сам корень c - k -кратным корнем многочлена f(x). Если k=1, то корень c называется простым корнем многочлена f(x).
Замечание 1.13.45. Понятие абстрактного линейного пространства мы детально рассмотрим в "Линейное пространство строк над полем" , после того как изучим ряд конкретных линейных пространств.
Понятие алгебры над полем (как кольца, являющегося к тому же и линейным пространством) будет рассмотрено в "Cтупенчатые системы линейных уравнений и метод Гаусса" .

