|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Стационарные временные ряды, модели авторегрессии - скользящего среднего
10.4. Условия стационарности для АРСС(p, q)-процесса
Рассмотрим простейшую модель - АР(1)-процесс вида

Пусть  - начальное условие. В главе 9 было показано (см. (9.8)), что
- начальное условие. В главе 9 было показано (см. (9.8)), что
Вычисляя математическое ожидание, получим:
Аналогично
При  и
и  получаем из (10.15) (см. главу 9):
получаем из (10.15) (см. главу 9):
Теперь для достаточно больших  из выражения (2.16) следует, что
из выражения (2.16) следует, что
Итак, АР(1)-процесс с течением времени имеет независимую от  среднюю, т.е.
среднюю, т.е.  .
.
Вычисляя дисперсию  , имеем из (2.17):
, имеем из (2.17):
Выражение (10.18) конечно и также не зависит от времени.
Наконец, вычислим автоковариации:
Итак, автоковариации предельных значений  также конечны и не зависят от времени.
также конечны и не зависят от времени.
Мы показали, что АР(1)-процесс с  слабо стационарны (далее - стационарны) в пределе. Это значит, что если при исследовании экономических временных рядов описываемые процессы имеют недолгую историю, велика опасность нестационарности. Осторожные исследователи часто исключают ранние наблюдения из анализа.
слабо стационарны (далее - стационарны) в пределе. Это значит, что если при исследовании экономических временных рядов описываемые процессы имеют недолгую историю, велика опасность нестационарности. Осторожные исследователи часто исключают ранние наблюдения из анализа.
Выпишем решение (9.9) уравнения АР(1) из главы 9 без использования начального условия  . Получаем:
. Получаем:
Вспомним, что произвольная постоянная C интерпретировалась как отклонение от долгосрочного равновесия. Ясно, что для стационарности необходимо, чтобы 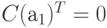 . Значит, либо
. Значит, либо 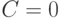 , либо
, либо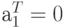 .
.
Итак, получаем условия стационарности:
- однородное решение должно быть равно нулю. Поэтому либо последовательность значений
 должна находиться бесконечно далеко от начала процесса
должна находиться бесконечно далеко от начала процесса 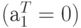 , либо процесс должен быть в состоянии равновесия;
, либо процесс должен быть в состоянии равновесия; - характеристический корень
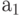 должен быть по абсолютной величине меньше 1.
должен быть по абсолютной величине меньше 1.
Эти два условия легко переносятся на общие АРСС(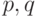 )-процессы. Однородное решение в общем случае имеет вид
)-процессы. Однородное решение в общем случае имеет вид
или в случае повторения корней
где
Рассмотрим теперь стационарные АРСС(2, 1)-модели
Можно показать, что если характеристические корни (10.21) лежат в единичном круге, то 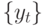 генерируют стационарную последовательность.
генерируют стационарную последовательность.
Обратимся к моделям скользящего среднего. Рассмотрим СС(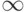 )-процесс (СС(
)-процесс (СС( )-процесс является частным случаем).
)-процесс является частным случаем).
Пусть
Ранее мы выяснили, что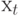 не является белым шумом. Теперь проверим условие стационарности:
не является белым шумом. Теперь проверим условие стационарности:
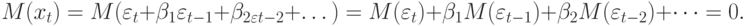
Повторяя процедуру с 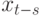 , имеем:
, имеем:
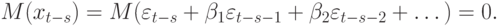
Далее
![D(x_{t}) = M[(\varepsilon _{t} + \beta _{1}\varepsilon _{t-1} + \beta _{2}\varepsilon _{t-2} +\dots )^{2}].](/sites/default/files/tex_cache/54b8f19a597baf9035a4d6987621a0a1.png)
Возведем выражение в скобках в квадрат и вычислим математическое ожидание, учитывая свойства белого шума:
![D(x_{t}) = M(\varepsilon _{t})^{2} + (\beta _{1})^{2}М(\varepsilon _{t-1})^{2} + (\beta _{2})^{2}М(\varepsilon _{t-2})^{2} = \sigma ^{2}[1 + (\beta _{1})^{2} + (\beta _{2})^{2} +\dots ].](/sites/default/files/tex_cache/e2bdc85ce5718f92ba9893a292d118f9.png)
Если ряд  сходится, то дисперсия конечна и не зависит от
сходится, то дисперсия конечна и не зависит от  .
.
Вычислим автоковариации:
![M(x_{t}, x_{t-s}) = M[(\varepsilon _{t} +\beta _{1}\varepsilon _{t}_{-1} + \beta _{2}\varepsilon _{t-2} +\dots )(\varepsilon _{t-s} + \beta _{1}\varepsilon _{t-s-1} + \beta _{2}\varepsilon _{t-s-2} +\dots )].](/sites/default/files/tex_cache/99aa16041cd9d8d49733a86a4f1e8e26.png)
Учитывая, что  для
для  , получим:
, получим:
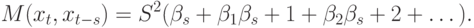
Если ряд в скобках сходится, то ковариация конечна и зависит только от величины сдвига  , но не от времени
, но не от времени  .
.
Суммируя сказанное получаем, что необходимые и достаточные условия стационарности заключаются в сходимости рядов:
Если полагать, что 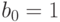 и
и  справедливо и для
справедливо и для 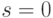 , то можно обойтись одним условием 2.
, то можно обойтись одним условием 2.
Отсюда сразу следует, что любой СС( )-процесс с конечным
)-процесс с конечным  всегда стационарен, так как ряд 2 в этом случае имеет конечное число слагаемых.
всегда стационарен, так как ряд 2 в этом случае имеет конечное число слагаемых.
Рассмотрим теперь авторегрессионную модель
Если все характеристические корни однородной части уравнения (10.22) находятся в пределах единичного круга, то частное решение можно представить формулой
где
Можно показать, что последовательность (\u03b1_{i}) является решением системы уравнений
\alpha _{i} - a_{i}\alpha _{i-1} - a_{2}\alpha _{i-2} -\dots - a_{p}\alpha _{i-p} = 0. (10.24)
Отметим, (10.24) является СС(q)-процессом. Сходимость ряда (10.23) влечет сходимость ряда
\alpha _{i}^{2. }Следовательно, можно использовать (10.23) для проверки трех условий стационарности. Отметим, что \alpha _{0} = 1.Итак:
Из главы 9 известно, что условие  является необходимым для того, чтобы характеристические корни лежали внутри единичного круга;
является необходимым для того, чтобы характеристические корни лежали внутри единичного круга;
Аналогично
Таким образом, средняя, дисперсия и ковариации конечны и не зависят от времени  и сдвига
и сдвига 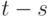 .
.
Ничего существенного не изменится, если соединить АР( )- и СС(
)- и СС( )-модели в общую АРСС(
)-модели в общую АРСС(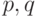 )-модель:
)-модель:
Если корни обратного характеристического уравнения лежат вне единичного круга (а значит, корни однородного характеристического уравнения в (10.25) лежат внутри единичного круга) и 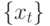 - стационарная последовательность, то
- стационарная последовательность, то 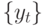 - тоже стационарная последовательность.
- тоже стационарная последовательность.

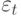

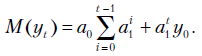


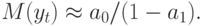
![D(y_{t}) = M(y_{t} -\mu )^{2} = M[(\varepsilon _{t} + a_{1}\varepsilon _{t-1} + (a_{1})^{2}\varepsilon _{t-2} +\dots +)^{2}] = \sigma ^{2}[1 + (a_{1})^{2} + (a_{1})^{4} +\dots ] = \sigma ^{2}/[1 - (a_{1})^{2}].](/sites/default/files/tex_cache/0a9faddfbbc0f5dc7d871f135654984f.png)
![M[(y_{t} - \mu )(y_{t-s} - \mu )] = M{(E_{t} + a_{1}E_{t-1} + (a_{1})^{2}E_{t-2} +\dots +) \cdot (E_{t-s} + a_{1} E_{t-s-1} +\\
+(a_{1})^{2}E_{t-s-2} +\dots +)] =\\
= \sigma ^{2}(a_{1})s[1 + (a_{1})^{2} + (a_{1})^{4} +\dots ] = \sigma ^{2}(a_{1})^{s}/[1 - (a_{1})^{2}].](/sites/default/files/tex_cache/95d618a2391d40c7536d0f0baa6d0673.png)
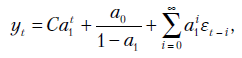

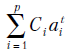
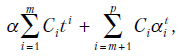

 ;
;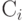
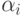
 ) различных корней.
) различных корней.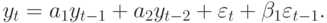


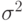 .
.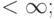
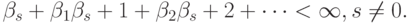
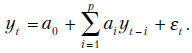
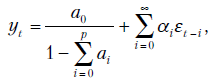
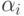
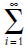
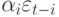


![cov(y_{t}, y_{t-s}) = M[(\varepsilon _{t} + \alpha _{1}\varepsilon _{t-1} + \alpha \varepsilon _{t-2} +\dots )\\
(\varepsilon _{t-s} +\alpha _{1}\varepsilon _{t-s} +\alpha _{2}\varepsilon _{t-s} +\dots )] = s^{2}\\
(\alpha _{s} +\alpha _{s+1}\alpha _{1} +\alpha _{s+2}\alpha _{2} +\dots ).](/sites/default/files/tex_cache/632a281dbe77229271c248547e93312e.png)

