|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Синтез тестов для комбинационных схем
Понятие критических кубов первоначально было введено для вентиля НЕ-И [16.8] и использовано при генерации тестов в системе LASAR. Далее это понятие было распространено на основные вентили [16.9,16.10]. При этом критические кубы для простых вентилей И, ИЛИ, НЕ, НЕ-И, НЕ-ИЛИ во всех работах одинаковы (хотя трактуются различно). Для более сложных логических элементов критические кубы в этих работах определены по-разному. Мы при определении критических кубов используем подход, близкий к предложенному в работе [16.8].
| Функция |  |
 |
 |
Аналитическая запись куба |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
 |
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
 |
||
 |
0 |  |
 |
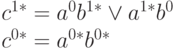 |
 |
0 |  |
||
 |
 |
 |
||
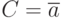 |
 |
- |  |
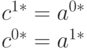 |
 |
- |  |
||
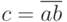 |
 |
1 |  |
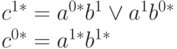 |
| 1 |  |
 |
||
 |
 |
 |
||
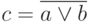 |
 |
 |
 |
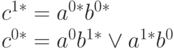 |
| 0 |  |
 |
||
 |
0 |  |
||
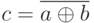 |
 |
1 |  |
 |
| 0 |  |
 |
||
 |
0 |  |
||
| 1 |  |
 |
||
 |
0 |  |
 |
|
| 0 |  |
 |
||
 |
1 |  |
||
| 1 |  |
 |
||
 |
 |
0 |  |

|
| 0 |  |
 |
||
 |
1 |  |
||
| 1 |  |
 |
||
 |
1 |  |
 |
|
| 0 |  |
 |
||
 |
0 |  |
||
| 1 |  |
 |
Для комбинационных ДУ основной алгоритм генерации тестов методом критических путей можно сформулировать следующим образом.
- Выбрать внешний выход схемы и присвоить ему критическое значение
 .
.
- Для элемента, имеющего критическое значение на выходе, выбирая соответствующие критические кубы из таблицы *-кубов его типа, распространить значения на входы элемента.
- Присвоить соответствующие значения выходам элементов, которые соединены с входами, получившими новые значения в п. 2. Выполнить операцию импликации для всех таких выходов.
- Если импликация показывает несовместимость вновь полученных значений со старыми (противоречивая ситуация), перейти к п. 5, иначе к п. 6.
- Вернуться к последнему выбору критических кубов. Если выбора нет (все варианты распространения критических значений рассмотрены), то перейти к п. 7, иначе выбрать *-куб и перейти к п. 3.
- Выбрать "необработанный" элемент с критическим выходом и вернуться к п. 2. Если таких элементов нет, перейти к п. 8.
- Для рассмотренного критического значения на внешнем выходе не существует выходного набора с критическими путями. Если это был
 ,
то внешнему выходу присвоить значение
,
то внешнему выходу присвоить значение  и вернуться к п. 2, если же -
и вернуться к п. 2, если же -  , то в случае наличия "необработанных" внешних выходов схемы вернуться к п. 1. Если все выходы обработаны, то конец.
, то в случае наличия "необработанных" внешних выходов схемы вернуться к п. 1. Если все выходы обработаны, то конец.
- Выполнить процедуру доопределения для оставшихся "неподтвержденными" некритических значений на выходах элементов.
- Если это невозможно вследствие несовместимости вновь полученных значений со старыми, то вернуться к п. 5. В противном случае (если набор построен) вернуться к п. 1; если на внешнем выходе был
 ,
то присвоить этому выходу значение
,
то присвоить этому выходу значение  и перейти к п. 2.
и перейти к п. 2.
Приведенный алгоритм порождает в лучшем случае по два набора для каждого выхода схемы. Для большей полноты теста можно получить дополнительные критические пути (соответственно наборы теста) с помощью того же алгоритма, отрабатывая в процессе генерации теста всевозможные варианты выбора критических кубов, как это было показано для схемы, изображенной на рис. 6.2.
Такова укрупненная общая схема алгоритма для комбинационных схем. Следует отметить, что в процессе реализации для ускорения генерации тестов целесообразно использовать некоторые эвристические приемы. Например, при выборе *-куба предпочтительней брать куб с критическими значениями для неисправностей, не проверенных к текущему моменту. При генерации нового набора теста для того же критического значения выхода целесообразно начинать не с самого начала, а с места последнего выбора варианта, сохраняя частично значения сигналов на линиях схемы, полученные на предыдущем наборе. Следует отметить, что там, где генерация теста требует многомерной активизации путей, этот метод не гарантирует построения теста.
После выполнения начального этапа генерации теста одним из приведенных методов выполняется моделирование схемы с неисправностями, определяется полнота теста и список непроверяемых неисправностей. Далее для непроверенных неисправностей используются методы генерации тестов для конкретной неисправности, которые применяются на заключительном этапе и рассматриваются ниже.
Ключевые термины:
Проверяющий тест - множество входных воздействий, проверяющее заданное множество неисправностей.
Псевдослучайный метод - основан на псевдослучайной генерации входных воздействий.
Критический куб - определяет зависимость выхода логического от его входов таким образом, что изменение значений на входах ведет к изменению значение сигнала на выходе элемента.
Краткие итоги
В лекции рассмотрена задача построения проверяющих тестов для комбинационных схем. Изложены методы генерации тестов, которые используются на начальном этапе построения проверяющего теста и не ориентированы на конкретную заданную неисправность.
В "Синтез тестов для комбинационных схем" описана общая архитектура, цели и задачи программной системы построения проверяющих тестов
В "Синтез тестов для комбинационных схем" представлен псевдослучайный метод построения проверяющего теста, который основан на псевдослучайной генерации входных наборов с последующей оценкой с помощью логического моделирования с неисправностями.
В "Синтез тестов для комбинационных схем" рассмотрен метод критических путей, который основан на активизации путей в схеме в обратном порядке от выходов ко входам схемы.
Вопросы и упражнения
- Чем структурные тесты отличаются от функциональных?
- Как генерируется новый входной набор в ПС-методе?
- Каким образом оценивается новый входной набор в ПС-методе?
- Какие вы можете предложить критерии окончания ПС-генерации тестов?
- Какие проблемы есть у ПС-генерации тестов для последовательностных схем?
- С какой вероятностью генерируются значения 0,1 для входов схемы?
- Как можно изменять вероятности значений 0,1 для входов схемы?
- Что такое критический куб?
- Приведите и объясните критические кубы для вентиля НЕ_И.
- Приведите и объясните критические кубы для вентиля ИЛИ.
- Приведите основной алгоритм построения теста методом критических кубов.
- Сколько входных наборов генерирует этот алгоритм для каждого выхода схемы?
- На каком этапе целесообразно использовать псевдослучайный метод генерации тестов?
- Для каких схем целесообразно применять метод критических кубов?
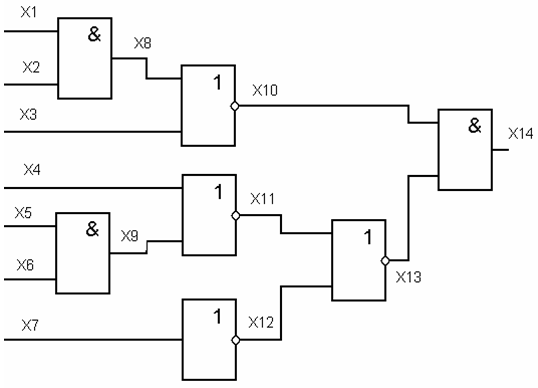
- Построить проверяющий тест для одиночных константных неисправностей схемы рис. 16.4 методом критических путей.