|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Синтез тестов для комбинационных схем
16.2 Псевдослучайный метод генерации тестов
Данный метод не ориентирован на конкретную неисправность и строит тест для всей схемы. Он относительно прост в реализации, обладает высоким быстродействием и для некоторых классов схем позволяет получить тесты с удовлетворительной полнотой (особенно это касается комбинационных схем). Этим обусловлено широкое применение этого метода в системах автоматизированного построения тестов [16.5]. Важнейшей компонентой этого метода является программа моделирования неисправных схем, которая позволяет отбирать тестовые воздействия из множества случайно генерируемых двоичных наборов. При реализации этого метода используются программные генераторы псевдослучайных двоичных чисел.
В простейшем случае псевдослучайный двоичный набор обрабатывается следующим образом. Для текущего случайного двоичного вектора 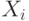 с помощью программы моделирования с неисправностями определяется величина
с помощью программы моделирования с неисправностями определяется величина 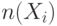 , которая характеризует число неисправностей, проверяемых на наборе
, которая характеризует число неисправностей, проверяемых на наборе 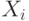 без учета тех неисправностей, которые проверяются ранее построенной тестовой последовательностью
без учета тех неисправностей, которые проверяются ранее построенной тестовой последовательностью 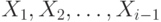 .
.
Далее если 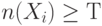 (порог), то набор
(порог), то набор 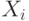 включается в тестовую последовательность и генерируется следующий псевдослучайный набор. Если
включается в тестовую последовательность и генерируется следующий псевдослучайный набор. Если 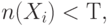 то этот входной набор бракуется и не включается в тест. Кроме этого, набор может браковаться и по некоторым другим причинам (например, если при переходе от предыдущего набора к текущему возникает опасное состязание сигналов). Этот процесс продолжается, пока не будет достигнута заданная пользователем полнота тестовой последовательности или пороговая величина длины или времени генерации теста.
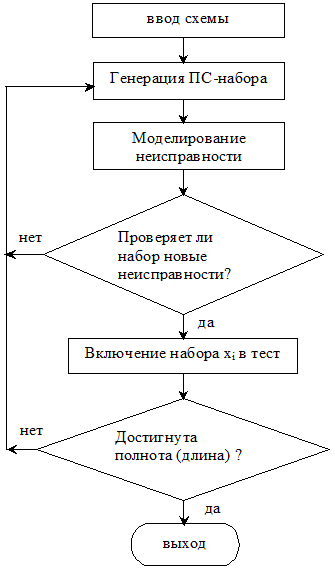
Упрощенная блок-схема алгоритма псевдослучайной генерации тестов представлена на рис. 16.2.
то этот входной набор бракуется и не включается в тест. Кроме этого, набор может браковаться и по некоторым другим причинам (например, если при переходе от предыдущего набора к текущему возникает опасное состязание сигналов). Этот процесс продолжается, пока не будет достигнута заданная пользователем полнота тестовой последовательности или пороговая величина длины или времени генерации теста.
Упрощенная блок-схема алгоритма псевдослучайной генерации тестов представлена на рис. 16.2.
В простейшем случае генерируется псевдослучайный набор, в котором каждый вход с равной вероятностью принимает значения 0,1. Но это не всегда эффективно. Поэтому в том случае, когда псевдослучайные наборы перестают проверять новые неисправности, то вероятности генерации 0,1 для входов схемы подстраиваются.
Кроме этого, был разработан ряд эвристических алгоритмов, которые генерируют псевдослучайные наборы с более сложным распределением вероятностей. При этом для каждого входного набора схемы рассчитываются вероятности подачи на него 0 и 1. Для определения этих вероятностей обычно на этапе препроцессорной обработки предварительно анализируют структуру схемы, либо используют адаптивные алгоритмы управления датчиками случайных чисел [16.7].
Следует отметить, что в процессе случайного поиска последовательностная схема может перейти в такое состояние, что найти входной набор, удовлетворяющий изложенным критериям трудно или даже невозможно. В этом случае нужно предусмотреть выход из этого тупикового состояния за счет включения входного набора, не удовлетворяющего приведенным критериям (проверяющие новые неисправности), но переводящего схему в новое состояние. В дальнейшем этот метод получил развитие в эволюционных алгоритмах генерации тестов, которые детально рассмотрены в "Эволюционные методы генерации тестов" .
16.2 Метод критических путей
Из структурных методов на начальном этапе хорошо зарекомендовали себя на практике алгоритмы, основанные на методе критических путей [16.8-16.10].
Они дают неплохую полноту теста и относительно просты в реализации. Метод основан на том, что половина одиночных константных неисправностей на критических (активизированных) путях проверяется тестом. Поэтому желательно строить тесты, порождающие как можно больше критических путей, на которых изменение сигнала на любой линии схемы, входящей в такой путь, вызывает изменение сигнала на выходе схемы. Такие тесты строятся с использованием так называемых критических кубов логических элементов схемы (они будут описаны ниже).
Начиная с выхода, где значение полагается равным  или
или  (звездочкой обозначается критичность), критические пути строятся по направлению к входам схемы. Для каждого логического элемента, выход которого получил критическое значение, осуществляется выбор критического куба - его входам присваиваются такие значения, чтобы один или более входов были критическими, т.е. чтобы при изменении значения на входе изменялось значение сигнала на выходе элемента. Например, если вентиль НЕ-И с входами
(звездочкой обозначается критичность), критические пути строятся по направлению к входам схемы. Для каждого логического элемента, выход которого получил критическое значение, осуществляется выбор критического куба - его входам присваиваются такие значения, чтобы один или более входов были критическими, т.е. чтобы при изменении значения на входе изменялось значение сигнала на выходе элемента. Например, если вентиль НЕ-И с входами 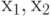 имеет значение на выходе
имеет значение на выходе 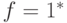 , то значения на его входах
, то значения на его входах  ,
, 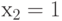 критичны по отношению к
критичны по отношению к 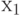 .
Аналогично входные значения
.
Аналогично входные значения 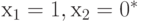 критичны по отношению к
критичны по отношению к 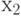 . Набор
. Набор 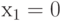 ,
, 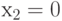 не имеет критических значений, так как изменение
не имеет критических значений, так как изменение 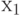 или
или
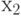 на единицу не вызывает изменения выхода вентиля
на единицу не вызывает изменения выхода вентиля  .
Если выход вентиля
.
Если выход вентиля  , то набор
, то набор  критичен по отношению к обоим входам.
Суть метода заключается в том, что мы пытаемся распространить критические значения от выхода схемы к входам с помощью критических кубов элементов.
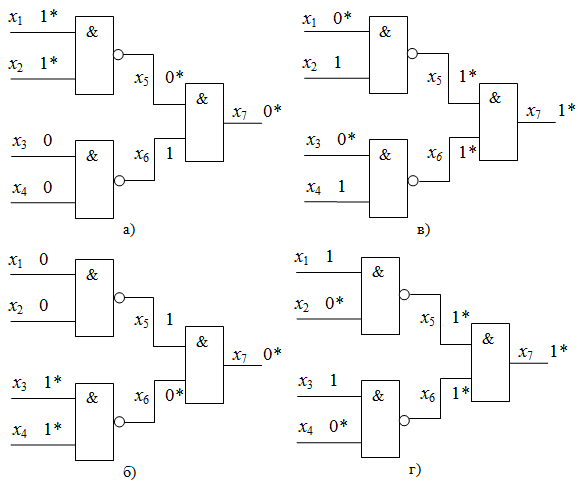
Прежде чем формально описать алгоритм генерации тестов методом критических путей, рассмотрим его на небольшом примере схемы, изображенной на рис. 16.3.
критичен по отношению к обоим входам.
Суть метода заключается в том, что мы пытаемся распространить критические значения от выхода схемы к входам с помощью критических кубов элементов.
Прежде чем формально описать алгоритм генерации тестов методом критических путей, рассмотрим его на небольшом примере схемы, изображенной на рис. 16.3.
Выбираем начальное значение выхода схемы  . Из табл. 6.1 критических кубов (методы их построения будут рассмотрены ниже) для вентиля И видно,
что существуют два критических куба со значениями на выходе
. Из табл. 6.1 критических кубов (методы их построения будут рассмотрены ниже) для вентиля И видно,
что существуют два критических куба со значениями на выходе 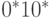 и
и 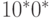 (здесь значения записаны в порядке
(здесь значения записаны в порядке  ).
Выбирая первый из них, получаем
).
Выбирая первый из них, получаем  ,
,
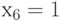 .
.
Из табл. 6.1 выбираем единственный для вентиля НЕ-И со значением  на выходе критический куб
на выходе критический куб 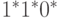 , который определяет
, который определяет  ,
,  .
Чтобы получить значение
.
Чтобы получить значение 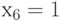 , из трех возможных комбинаций значений входов выбираем
, из трех возможных комбинаций значений входов выбираем 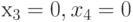 .
Таким образом, мы получили тестовый набор
.
Таким образом, мы получили тестовый набор 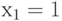 ,
, 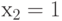 ,
, 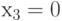 ,
, 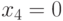 .
Очевидно, что этот набор проверяет одиночные константные неисправности, противоположные критическим значениям, т.е. если линия помечена
.
Очевидно, что этот набор проверяет одиночные константные неисправности, противоположные критическим значениям, т.е. если линия помечена  , то проверяется неисправность const0 на этой линии. Если же она помечена
, то проверяется неисправность const0 на этой линии. Если же она помечена  , то проверяется неисправность соnst1. На рис. 6.2 приведены еще три набора, которые построены аналогичным способом и вместе с первым набором составляют полный проверяющий тест на одиночные константные неисправности для рассматриваемой схемы.
, то проверяется неисправность соnst1. На рис. 6.2 приведены еще три набора, которые построены аналогичным способом и вместе с первым набором составляют полный проверяющий тест на одиночные константные неисправности для рассматриваемой схемы.