|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Логическое моделирование
Состав и назначение программ логического моделирования
Логическое моделирование представляет собой процедуру проверки функционирования логической схемы с помощью компьютера. Его основная цель состоит в том, чтобы проверить функцию проектируемой логической схемы без ее физической реализации, поскольку после изготовления схемы внесение изменений в нее при современной технологии сделать нелегко и недешево. Верификация выполняется путем сравнения результатов моделирования, полученных для проектируемого ДУ, со спецификацией. При этом проверяются как логические функции, так и временные соотношения.
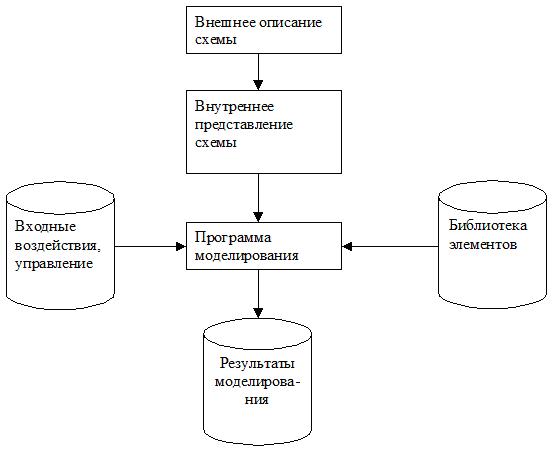
Логическое моделирование включает в себя построение математической модели ДУ - системы соотношений, описывающей поведение исследуемого устройства с заданной точностью, и дальнейший анализ поведения этой модели на заданной последовательности входных воздействий. При решении задач анализа и диагностирования ДУ обычно используется структурная математическая модель объекта, отражающая совокупность компонентов объекта, связи между компонентами и связь объекта с внешней средой. Для выполнения логического моделирования необходимы следующие компоненты, представленные на рис.3.1 :
- модель ДУ,
- входные воздействия,
- библиотека логических элементов,
- результаты моделирования.
Здесь внешнее описание схемы (графическое либо текстовое на специализированном языке) транслируется во внутреннее представление модели ДУ, которое непосредственно используется в процессе моделирования. Входные воздействия также могут быть описаны графически с помощью временных диаграмм либо текстом на специализированном языке. Важнейшей компонентой является библиотека моделей логических элементов, состав которой во многом определяет возможности системы моделирования. Результатом является изменение сигналов во времени для внешних и внутренних переменных модели в виде таблиц или временных диаграмм, которые записываются на диск.
Логическое моделирование является важнейшей компонентой САПР цифровых систем. С помощью логического моделирования в системах автоматизированного проектирования и диагностирования ДУ исследуются следующие проблемы [ 2.2 ] :
- проверка правильности логического функционирования ДУ;
- проверка функционирования цепей установки ДУ;
- проверка временных характеристик ДУ;
- анализ состязаний сигналов;
- определение полноты теста и списка непроверенных неисправностей;
- определение диагностических свойств тестов;
- получение диагностической информации для локализации неисправностей ДУ.
При верификации ДУ с помощью логического моделирования необходимо решить следующие проблемы:
- построение необходимых входных воздействий (генерация тестов);
- определение корректности полученных результатов;
- определение качества используемых входных воздействий (например, полнота проверяющих тестов и т.п.).
Основным математическим аппаратом, применяемым в исследовании цифровых логических схем, является теория булевых функций. При этом функционирование ДУ моделируется в двоичном алфавите 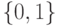 , что достаточно точно отражает их поведение в статике для установившихся значений сигналов. Однако такие модели не учитывают переходные процессы, возникающие при смене значений входных сигналов и обусловленные временными характеристиками элементов. Поэтому при исследовании переходных процессов получили распространение многозначные алфавиты, которые позволяют решать эти задачи с известной степенью адекватности логическими средствами без явного задания задержек элементов. Отметим, что в случае анализа переходных процессов мы имеем ДУ в два разные (предыдущий и настоящий) моменты времени и множество линий, на которых значения сигналов в эти моменты различны (или могут быть различны) вследствие изменения некоторых входных сигналов. С другой стороны, при синтезе тестов мы имеем одно ДУ в двух различных технических состояниях (исправное и неисправное) и множество линий схемы, на которых значения сигналов в этих состояниях различны (или могут быть различны) вследствие наличия в некоторых элементах неисправностей. В обоих случаях мы исследуем логическую зависимость в ДУ: при моделировании вследствие изменения входных сигналов, при генерации тестов – эффект влияния неисправностей. Поэтому, в силу одинаковой математической природы при построении тестов также широко используются многозначные алфавиты. В обоих случаях анализ двух ДУ в двоичном (иногда троичном) алфавите заменяется анализом одного устройства в многозначном алфавите.
, что достаточно точно отражает их поведение в статике для установившихся значений сигналов. Однако такие модели не учитывают переходные процессы, возникающие при смене значений входных сигналов и обусловленные временными характеристиками элементов. Поэтому при исследовании переходных процессов получили распространение многозначные алфавиты, которые позволяют решать эти задачи с известной степенью адекватности логическими средствами без явного задания задержек элементов. Отметим, что в случае анализа переходных процессов мы имеем ДУ в два разные (предыдущий и настоящий) моменты времени и множество линий, на которых значения сигналов в эти моменты различны (или могут быть различны) вследствие изменения некоторых входных сигналов. С другой стороны, при синтезе тестов мы имеем одно ДУ в двух различных технических состояниях (исправное и неисправное) и множество линий схемы, на которых значения сигналов в этих состояниях различны (или могут быть различны) вследствие наличия в некоторых элементах неисправностей. В обоих случаях мы исследуем логическую зависимость в ДУ: при моделировании вследствие изменения входных сигналов, при генерации тестов – эффект влияния неисправностей. Поэтому, в силу одинаковой математической природы при построении тестов также широко используются многозначные алфавиты. В обоих случаях анализ двух ДУ в двоичном (иногда троичном) алфавите заменяется анализом одного устройства в многозначном алфавите.
Общие принципы логического моделирования
Исходной информацией для программ логического моделирования является описание схемы ДУ в виде сети, вершинами которой являются логические элементы, входы и выходы. Практически каждая система моделирования имеет свои языковые средства для описания схемы ДУ и входных воздействий (тестов).
Далее описание схемы транслируется в некоторое внутреннее машинное представление, которое позволяет эффективно выполнять собственно процесс моделирования. Существует два основных типа машинных моделей схемы: табличная и программная. В соответствии с этим используются два метода моделирования: интерпретативный и компилятивный. Интерпретативное моделирование использует модель схемы в виде ряда таблиц, связанных системой ссылок, является более универсальным и позволяет проводить более точный временной анализ. Пример основной структуры данных, используемой при этом методе моделирования, можно найти в "Машинные модели логических схем и управление процессом моделирования " . Компилятивный метод моделирования использует готовую скомпилированную машинную программу и поэтому является более быстродействующим за счёт сокращения операций поиска адресов нужных значений сигналов и вызовов подпрограмм, которые составляют существенную часть в интерпретативном методе.
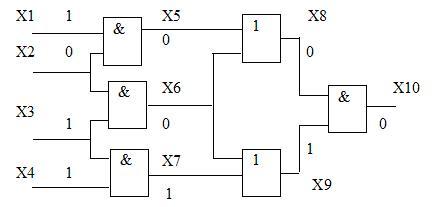
Процесс логического моделирования состоит из подачи на внешние входы модели ДУ некоторого входного воздействия и последовательного от входов схемы к ее выходам вычисления значений выходов логических элементов и получения, таким образом, выходной реакции на заданное входное воздействие. На рис.3.2 представлен простой пример комбинационной схемы с результатами логического моделирования в двоичном алфавите для одного входного набора (соответствующий одному моменту времени).
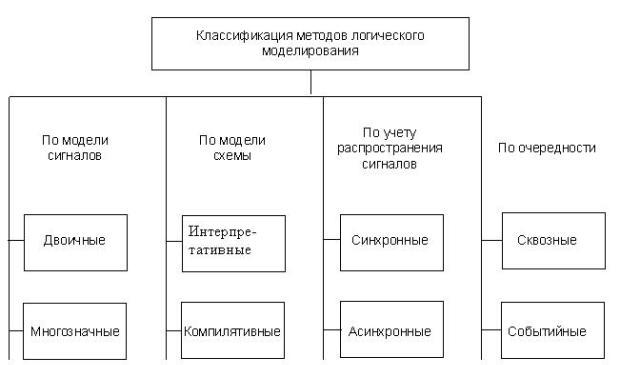
Этот процесс может быть организован по-разному в зависимости от применяемых методов моделирования. Основными отличительными чертами методов логического моделирования являются: модель сигналов, модель схемы в компьютере, способ учета времени распространения сигналов в ДУ, управление очерёдностью моделирования логических элементов [ 2.2 ] . В зависимости от применяемых моделей сигналов, методы делятся: по алфавиту – на двоичные и многозначные; по используемой модели схемы в компьютере – на интерпретативные и компилятивные; по учёту распространения сигналов – на синхронные (без учета задержек логических элементов) и асинхронные (с учетом задержек); по очередности моделирования логических элементов – сквозные и событийные [ 1.2 ] . Классификация методов моделирования представлена на рис.3.3 .
Основными характеристиками алгоритмов логического моделирования является адекватность, быстродействие и объём памяти, необходимый при реализации. При этом под адекватностью понимается степень соответствия результатов моделирования реальному поведению исследуемого ДУ. Для комбинационных ДУ все алгоритмы логического моделирования гарантируют высокую адекватность установившихся значений сигналов. Моделирование последовательностных ДУ может давать результаты различной степени адекватности из-за различных моделей задержек элементов, неопределенности начальных состояний и явления состязаний сигналов, что существенно осложняет моделирование таких устройств.
Адекватность моделирования зависит, в основном, от используемой модели ДУ, моделей логических элементов и сигналов, способа учёта временных соотношений между сигналами. Обычно повышение степени адекватности связано со снижением быстродействия и увеличением необходимого объёма памяти. Самыми быстрыми являются алгоритмы двоичного моделирования в алфавите 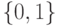 без учёта задержек, где реальный порядок срабатывания элементов не принимается во внимание. Учёт задержек элементов снижает быстродействие. Анализ переходных процессов требует увеличения значности алфавита.
без учёта задержек, где реальный порядок срабатывания элементов не принимается во внимание. Учёт задержек элементов снижает быстродействие. Анализ переходных процессов требует увеличения значности алфавита.
Модели сигналов
В процессе моделирования входные, выходные и внутренние переменные логических элементов схемы принимают значения из алфавита моделирования, используемого в данной системе моделирования. Моделью сигнала называют соответствие между символами алфавита и реальными физическими сигналами.
Простейшим является двоичный алфавит 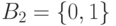 , в котором, как правило,
, в котором, как правило,  соответствует низкому уровню сигнала, а
соответствует низкому уровню сигнала, а  – высокому.
– высокому.
Для учета неоднозначности поведения ДУ часто используют троичный алфавит 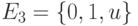 (
рис.
2.4), где символ u обозначает неизвестное или неопределенное значение сигнала (
(
рис.
2.4), где символ u обозначает неизвестное или неопределенное значение сигнала ( или
или  , но неизвестно, что именно). Символ u обычно используется для моделирования неопределённых, в том числе и начальных, состояний элементов памяти и неопределенностей, обусловленных явлением состязания сигналов, возникающих при переходных процессах, вызванных сменой входных воздействий.
, но неизвестно, что именно). Символ u обычно используется для моделирования неопределённых, в том числе и начальных, состояний элементов памяти и неопределенностей, обусловленных явлением состязания сигналов, возникающих при переходных процессах, вызванных сменой входных воздействий.
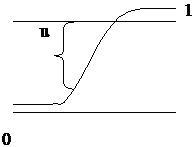
Кроме троичного применяется пятизначный алфавит 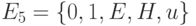 , представленный на рис.3.5 , где
, представленный на рис.3.5 , где  – низкий уровень сигнала;
– низкий уровень сигнала;  – высокий;
– высокий; 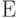 – гладкий переход из
– гладкий переход из  в
в  (передний фронт);
(передний фронт);  – гладкий переход из
– гладкий переход из  в
в  (задний фронт);
(задний фронт);  – неопределённое значение сигнала.
– неопределённое значение сигнала.
Для некоторых технологий (например, КМОП) моделирование даже определенных сигналов в статике требует введения дополнительных символов. Так иногда используют алфавит 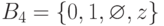 , где символ
, где символ  соответствует состоянию высокого импеданса для схем с отключающимся выходом, а
соответствует состоянию высокого импеданса для схем с отключающимся выходом, а  – конфликту на шине
[
1.2
]
. В настоящее время существует множество многозначных алфавитов, которые применяются в логическом моделировании и генерации тестов. Большая часть из них включается в универсальную систему многозначных алфавитов, которая представлена в
"Система многозначных алфавитов и функций"
.
– конфликту на шине
[
1.2
]
. В настоящее время существует множество многозначных алфавитов, которые применяются в логическом моделировании и генерации тестов. Большая часть из них включается в универсальную систему многозначных алфавитов, которая представлена в
"Система многозначных алфавитов и функций"
.
Ключевые термины:
Логическое моделирование – моделирование поведения логической схемы на заданных входных воздействиях.
Модель сигналов – представляется алфавитом моделирования, символы которого представляют физические сигналы.
Краткие итоги
Лекция является вводной в логическое моделирование цифровых схем, где определены основные понятия, которые затем используются в курсе лекций.
В разделе 3.1 описан состав и назначение основных модулей программной системы логического моделирования, определяются задачи, решаемые такой системой.
В разделе 3.2 изложены общие принципы и классификация методов логического моделирования по:
- модели сигналов;
- модели схемы;
- учету распространения сигналов;
- очередности обработки элементов.
В разделе 3.3 представлены модели сигналов, которые включают:
- двоичный алфавит;
- троичный алфавит;
- пятизначный алфавит.
Вопросы и упражнения
- Что такое логическое моделирование?
- Что необходимо для выполнения логического моделирования?
- Приведите структуру системы логического моделирования.
- Какие задачи решаются с помощью логического моделирования?
- Приведите классификацию методов логического моделирования.
- Приведите основные характеристики логического моделирования.
- Что такое модель сигнала?
- Чем отличается троичный алфавит от двоичного?
- Опишите пятизначный алфавит и физический смысл его символов.