|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Моделирование неисправностей задержек распространения сигналов
14.1 Задержка распространения сигнала
С внедрением КМОП-технологии возник новый класс физических неисправностей, которые проявляются в изменении времени распространения сигналов [14.1]. Правильное функционирование цифрового устройства возможно только в том случае, если времена распространения сигналов вдоль путей логической схемы лежат в определенных пределах. Когда время распространения сигнала выходит за эти пределы, говорят, что имеет место неисправность типа изменения задержки сигнала. В подавляющем большинстве эти неисправности приводят к увеличению времени распространения сигналов. Поэтому мы будем рассматривать только неисправности типа увеличения задержки сигналов. Предложено два типа моделей для подобных неисправностей. Первая модель, например, используемая в работе [14.2], оперирует с задержками сигналов логических элементов. Вторая - с задержками сигналов путей логических схем. Мы будем использовать второй тип модели - задержки сигналов вдоль путей, который был обоснован в работе [14.1]. В настоящем разделе будет показано как универсальные многозначные модели, разработанные в "Система многозначных алфавитов и функций" , могут быть использованы для моделирования данных неисправностей.
Обычно различают неисправности типов задержка переднего фронта (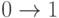 ) и задержка заднего фронта (
) и задержка заднего фронта (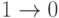 ). В определенном смысле задержка переднего фронта соответствует неисправности const0, так как она в течение некоторого времени ведет себя также как эта константная неисправность. Если это время значительно, то при задержке переднего фронта схема ведет себя почти также как и при неисправности const0 (в случае ее проверяемости). Аналогично задержка заднего фронта соответствует неисправности const1.
). В определенном смысле задержка переднего фронта соответствует неисправности const0, так как она в течение некоторого времени ведет себя также как эта константная неисправность. Если это время значительно, то при задержке переднего фронта схема ведет себя почти также как и при неисправности const0 (в случае ее проверяемости). Аналогично задержка заднего фронта соответствует неисправности const1.
Наиболее распространенный метод обнаружения неисправностей задержка сигналов заключается в следующем. Сначала на схему подается в момент времени 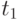 входной набор
входной набор 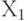 . После стабилизации сигналов в схеме в момент времени
. После стабилизации сигналов в схеме в момент времени 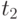 подается второй входной набор
подается второй входной набор 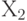 . При этом передний фронт сигнала распространяется вдоль проверяемых путей в схеме от внешних входов к внешним выходам. Измеряя реальную задержку распространения сигналов и сравнивая ее с эталонной, можно обнаружить неисправности задержки распространения сигналов тестируемых путей в схеме. Таким образом для проверки подобных неисправностей необходима пара входных наборов
. При этом передний фронт сигнала распространяется вдоль проверяемых путей в схеме от внешних входов к внешним выходам. Измеряя реальную задержку распространения сигналов и сравнивая ее с эталонной, можно обнаружить неисправности задержки распространения сигналов тестируемых путей в схеме. Таким образом для проверки подобных неисправностей необходима пара входных наборов 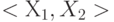 . Значения сигналов в схеме, установившиеся на наборе
. Значения сигналов в схеме, установившиеся на наборе 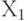 будем называть начальными значениями для пары
будем называть начальными значениями для пары 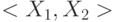 . Аналогично определим конечные значения,
которые устанавливаются на наборе
. Аналогично определим конечные значения,
которые устанавливаются на наборе 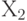 (в схеме не содержащей неисправности типа задержка сигнала).
(в схеме не содержащей неисправности типа задержка сигнала).
14.2 Устойчивые и неустойчивые тесты
Согласно [14.1] пару входных наборов 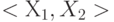 будем называть устойчивым тестом для задержки распространения сигналов по пути
будем называть устойчивым тестом для задержки распространения сигналов по пути 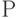 , если она проверяет эту неисправность независимо от других неисправностей типа задержка сигнала, не расположенных на данном пути
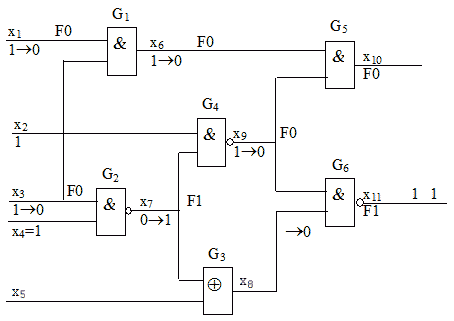
, если она проверяет эту неисправность независимо от других неисправностей типа задержка сигнала, не расположенных на данном пути 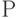 . Например, для схемы, представленной на рис. 14.1, пара наборов
. Например, для схемы, представленной на рис. 14.1, пара наборов 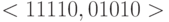 (значения даны в порядке
(значения даны в порядке 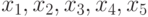 ) является устойчивым тестом для неисправности задержки пути
) является устойчивым тестом для неисправности задержки пути
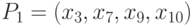 .
Анализ поведения схемы на этой паре наборов показывает, что задержка на пути
.
Анализ поведения схемы на этой паре наборов показывает, что задержка на пути 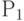 будет обнаружена независимо от наличия задержек на других путях схемы (например, на путях
будет обнаружена независимо от наличия задержек на других путях схемы (например, на путях 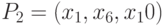 или
или 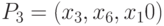 ). Важность понятия устойчивого теста обуславливается тем, что в реальных схемах задержки распространения сигналов могут изменяться вследствие технологических причин. Поэтому для того, чтобы неисправность задержки данного пути не была компенсирована другими неисправностями, необходимо использовать устойчивые тесты.
). Важность понятия устойчивого теста обуславливается тем, что в реальных схемах задержки распространения сигналов могут изменяться вследствие технологических причин. Поэтому для того, чтобы неисправность задержки данного пути не была компенсирована другими неисправностями, необходимо использовать устойчивые тесты.
Согласно [14.1], пару входных наборов будем называть неустойчивым тестом для задержки распространения сигналов по пути 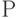 , если она проверяет эту неисправность при условии, что входы логических элементов пути
, если она проверяет эту неисправность при условии, что входы логических элементов пути 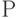 , не принадлежащие ему, принимают конечные значения до того, как изменение сигнала вдоль пути
, не принадлежащие ему, принимают конечные значения до того, как изменение сигнала вдоль пути 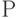 достигает этих элементов. Например, на рис. 14.1 указанная выше пара наборов является неустойчивым тестом для неисправности "задержка распространения сигнала" вдоль пути
достигает этих элементов. Например, на рис. 14.1 указанная выше пара наборов является неустойчивым тестом для неисправности "задержка распространения сигнала" вдоль пути 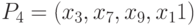 , так как она проверяет ее при условии, что значение сигнала на
, так как она проверяет ее при условии, что значение сигнала на 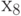 установится в 1 до прибытия на элемент
установится в 1 до прибытия на элемент 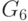 изменения сигнала вдоль пути
изменения сигнала вдоль пути 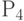 .
Отметим, что эта пара наборов для задержки сигналов путей
.
Отметим, что эта пара наборов для задержки сигналов путей 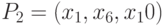 и
и 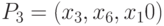 не является даже устойчивым тестом.
не является даже устойчивым тестом.
Непосредственно из определения неустойчивого теста вытекает следующее. Для того, чтобы пара наборов была неустойчивым тестом пути 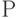 необходимо и достаточно выполнение условия всех элементов
необходимо и достаточно выполнение условия всех элементов 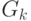 пути
пути
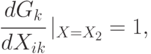
где 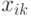 - вход
- вход 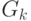 , принадлежащий пути [14.2], где
, принадлежащий пути [14.2], где 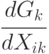 означает булеву производную
означает булеву производную 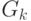 по переменной
по переменной  ,определение которой представлено в
"Синтез тестов для заданной неисправности"
.
Это условие показывает, что выход элемента
,определение которой представлено в
"Синтез тестов для заданной неисправности"
.
Это условие показывает, что выход элемента 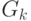 должен зависеть от входа
должен зависеть от входа 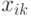 , на который приходит изменение сигнала по пути
, на который приходит изменение сигнала по пути 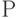 , при конечных (установившихся) значениях остальных входов этого элемента. Для устойчивого теста данное условие является необходимым, но недостаточным.
Например, для элемента
, при конечных (установившихся) значениях остальных входов этого элемента. Для устойчивого теста данное условие является необходимым, но недостаточным.
Например, для элемента 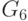 схемы рис. 14.1 это условие выполняется, но пара наборов
схемы рис. 14.1 это условие выполняется, но пара наборов 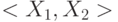 не является устойчивым тестом для пути
не является устойчивым тестом для пути 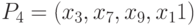 . Можно показать, что кроме приведенного выше условия необходимо, чтобы на паре
. Можно показать, что кроме приведенного выше условия необходимо, чтобы на паре 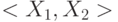
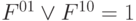 (где
(где 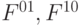 - ориентированные булевы дифференциалы [14.2] ) .
- ориентированные булевы дифференциалы [14.2] ) .