|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Синтез тестов для комбинационных схем
Генерация проверяющих тестов даже для комбинационных схем цифровых систем является сложной как в математическом, так и в техническом плане проблемой. Ее важнейшими аспектами являются:
- стоимость генерации тестов;
- качество генерируемых тестов;
- стоимость тестирования схемы с помощью построенных вход-выходных последовательностей.
Прежде всего, следует различать функциональные и структурные тесты. Алгоритмы построения функциональных тестов генерируют полное множество всевозможных тестовых наборов, которые позволяют полностью проверить функцию, реализуемую данной схемой. Например, для комбинационной схемы с  входами и одним выходом функциональным тестом является множество всевозможных
входами и одним выходом функциональным тестом является множество всевозможных 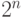 тестовых двоичных наборов, позволяющее восстановить булеву функцию, которая реализуется тестируемой схемой. Очевидно, что для схем большой размерности такой подход не всегда приемлем.
тестовых двоичных наборов, позволяющее восстановить булеву функцию, которая реализуется тестируемой схемой. Очевидно, что для схем большой размерности такой подход не всегда приемлем.
С другой стороны, структурные тесты проверяют только минимально необходимое множество неисправностей (как правило, одиночных константных неисправностей после процедуры сокращения списка, изложенной в "Модели логических элементов" ). Далее мы, в основном, будем рассматривать структурные тесты.
В теоретическом аспекте показано [16.1], что генерация тестов относится к классу NP-полных проблем (т.е. переборного типа), для которых не существует алгоритмов решения полиномиальной сложности. В практическом аспекте сложность ее решения зависит от применяемого алгоритма генерации теста. Эффективность разрабатываемых алгоритмов принято проверять на схемах из различных международных каталогов (benchmarks): ISCAS85 [16.2], ISCAS89 [16.3], ITC99 [16.4] и др. Псевдослучайные методы генерации тестов имеют низкую сложность алгоритма, но дают длинные тестовые последовательности и невысокую полноту. Детерминированные методы генерации дают тесты лучшего качества, но имеют большую сложность. Качество построенных тестов определяется, как правило, с помощью программ моделирования неисправных схем, в которых реализуются методы, рассмотренные в предыдущем разделе. Непосредственно процесс тестирования производится на специальном оборудовании - тестерах, которые обеспечивают подачу входных тестовых воздействий на схемы, съем выходных сигналов и их сравнение с эталонными значениями. Важнейшими характеристиками тестеров являются тактовая частота и объем памяти для хранения тестовых воздействий.
Структурные методы генерации тестов разделяются на два класса:
- построение теста для схемы в целом безотносительно конкретной неисправности;
- построение теста для конкретной заданной неисправности.
В первом разделе рассматривается структура системы генерации тестов, в последующих двух "Синтез тестов для комбинационных схем" -16.3 описаны методы построения тестов, которые используются на начальном этапе генерации проверяющих тестов для всей схемы. В последующих разделах будут изложены методы построения тестов для конкретной неисправности, которые, как правило, используются на заключительном этапе генерации тестов. С нашей точки зрения, их целесообразно применять на последнем этапе, когда осталось относительно небольшое число непроверенных неисправностей. На начальном этапе лучше применять другую стратегию. Нужны быстродействующие и простые в реализации методы построения тестов, которые позволяют с малыми затратами времени получить тест для большей части неисправностей. Одним из таких методов является псевдослучайный метод генерации тестов, достаточно подробно описанный в литературе [16.5,16.6].
16.1 Системы генерации тестов
Целью автоматизированной системы генерации тестов является построение проверяющего теста для данной схемы. При этом желательно, чтобы:
- полнота построенного теста была максимальна;
- стоимость генерации тестов (процессорное время) была минимальна;
- полученный тест имел минимальную длину.
Это вытекает из экономических требований. Полнота теста непосредственно влияет на качество производимой продукции. Длина теста влияет на стоимость тестирования ЦУ и определяет характеристики необходимых тестеров и время тестирования.
Следует отметить, что полнота теста должна определяться относительно проверяемых (неизбыточных) неисправностей. Так, например, для схемы, имеющей 5% избыточных несправностей, полнота теста 96% является явно недостижимой. Потому иногда различают полноту и эффективность теста, которые определяются следующим образом. Полнота - 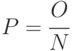 , где
, где  - общее число неисправностей и
- общее число неисправностей и  - число проверяемых на данном тесте неисправностей. Эффективность -
- число проверяемых на данном тесте неисправностей. Эффективность - 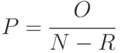 , где
, где  - число избыточных неисправностей.
- число избыточных неисправностей.
Количественные значения полноты (и эффективности) теста, очевидно, также существенно зависит от того, как формировалось множество неисправностей. Современные системы, как правило, используют методы сокращения списков неисправностей, основанные на отношениях эквивалентности и доминирования, которые были рассмотрены в "Модели логических элементов" .
Современная система генерации тестов включает в себя следующие основные компоненты:
- Программы генерации тестов, которые позволяют быстро получить на первом этапе начальную тестовую последовательность и работают со схемой в целом, а не ориентированы на конкретную неисправность;
- Программы моделирования неисправных схем, позволяющие на текущий момент оценить достигнутую полноту теста и определить множество непроверенных неисправностей, для которых необходимо достроить тест;
- Программы построения теста для конкретной заданной неисправности, которые используются на втором этапе генерации теста при его "доводке" до необходимой полноты;
- Программы сжатия тестов, которые позволяют компактно объединить фрагменты тестов, полученных на различных этапах.
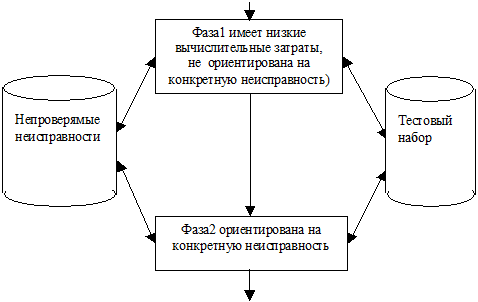
Структура системы генерации тестов представлена на рис. 16.1. Здесь в первой фазе обычно используются псевдослучайные алгоритмы (или методы критических путей и т.п.), которые достаточно быстро позволяют достичь приемлемой полноты начального теста 50-80%. После этого выполняется моделирование неисправностей и определяется множество непроверенных неисправностей, которое обрабатывается на втором этапе.
Псевдокод укрупненного алгоритма генерации тестов первого этапа представлен ниже.
Первая фаза заканчивается при достижении необходимой для первой фазы полноты теста, определяемой пользователем, либо вследствие лимита времени. При этом число неисправностей, проверяемых одним тестовым набором, сначала достаточно велико, а затем быстро уменьшается. Соответственно число не включенных в тест входных наборов быстро возрастает. В конце первой фазы формируется множество непроверенных неисправностей, тесты для которых далее генерируются во второй фазе.
Первая фаза(схема)
{
While(полнота или время не достигнуты)
{
Генерация теста(t);
Моделирование неисправностей(t);
p=число вновь проверяемых неисправностей(t);
if(p приемлемо) then включение t в тест;
}
}
Вторая фаза(схема, множество неисправностей)
{
while(есть необработанные неисправности)
{
выбор новой неисправности f;
генерация теста t для f;
if(тест для f построен) then
{
включение t в тест;
моделирование неисправностей на наборе t;
исключение неисправностей, проверяемых t;
}
}
}
Выше представлен псевдокод второй фазы генерации теста. При построении теста для данной неисправности можно использовать один из рассмотренных выше методов. Следует отметить, что время генерации теста для текущей неисправности необходимо контролировать.
Если оно превышает некоторый задаваемый пользователем порог, то неисправность исключается из дальнейшей обработки и объявляется непроверяемой. Наибольшие затраты времени имеют место для избыточных несправностей, для которых в худшем случае может потребоваться полный перебор всевозможных входных значений.
Поэтому имеет смысл на этапе препроцессорной обработки схемы, по-возможности, найти и исключить из дальнейшей обработки избыточные неисправности. Существенное влияние на эффективность генерации теста оказывает также метод выбора новой неисправности. Обычно выбираются неисправности, расположенные как можно ближе к внешним входам схемы. Это обусловлено тем, что построенный для такой неисправности тест активизирует в схеме длинный путь и потому проверяет больше несправностей.
Это ведет к болем коротким тестовым последовательностям. Вторая фаза заканчивается, когда обработаны все неисправности из определенного в первой фазе множества. Но возможен и досрочный останов из-за превышения лимитов процесорного времени или длины теста.