|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Выполнимость булевых функций и бинарные диаграммы в построении тестов
21.1 Выполнимость булевых функций
Рассмотренные ранее методы построения проверяющих тестов для заданной неисправности комбинационной схемы можно разбить на два класса:
- структурные методы, осуществляющие поиск решения непосредственно по логической схеме на основе активизации путей;
- аналитические методы, где построение теста выполняется путем манипуляций с формулами (метод различающей функции и булевых производных).
Относительно недавно разработан метод построения тестов на основе решения задачи выполнимости булевых функций [21.1], который занимает промежуточное положение между этими двумя подходами. Здесь строится различающая функция между булевыми функциями, реализующими исправную и неисправную схемы, которая далее преобразуется в конъюнктивную нормальную форму (КНФ) и решается задачи выполнимости КНФ.
Рассмотрим задачу построения КНФ по заданной логической схеме [21.1,21.2]. Для начала возьмем уравнение 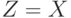 .
В логических терминах это уравнение эквивалентно следующему:
.
В логических терминах это уравнение эквивалентно следующему: 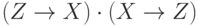 . Но в выражение
. Но в выражение 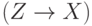 эквивалентно
эквивалентно 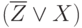 , поэтому
, поэтому 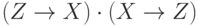 можно представить в виде
можно представить в виде 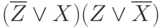 . Заметим, чтобы это выражение приняло значение "истина", необходимо чтобы оба значения
. Заметим, чтобы это выражение приняло значение "истина", необходимо чтобы оба значения  и
и  были истинны, либо наоборот оба значения были ложными.
были истинны, либо наоборот оба значения были ложными.
Далее рассмотрим уравнение  для вентиля И, которое можно преобразовать к виду
для вентиля И, которое можно преобразовать к виду 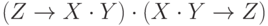 [21.1,21.2]. Действуя по приведенной выше схеме, на следующем шаге получаем
[21.1,21.2]. Действуя по приведенной выше схеме, на следующем шаге получаем

В полученной КНФ отдельные дизъюнкты (сомножители) могут иметь один, два или три терма ("слагаемых"). Известно[21.1,21.2], что подобные преобразования можно выполнить для типовых логических вентилей - окончательные результаты представлены в табл. 21.1
| Формула | Тип вентиля |
|---|---|
| буфер | |
| инвертор | |
| Двухвходовой И | |
| Двухвходовой НЕ-И | |
| Двухвходовой ИЛИ | |
| Двухвходовой НЕ-ИЛИ | |
| Двухвходовой ИЛИ |
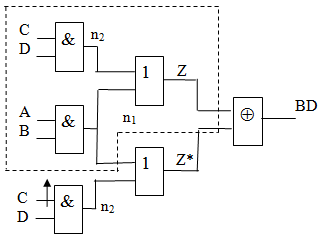
Далее перейдем от преобразования отдельных логических элементов к схеме в целом на примере схемы рис. 21.1[21.2]. Здесь исходная (исправная) схема выделена пунктиром.
Поведение этой (исправной) схемы может быть описано с помощью следующей КНФ
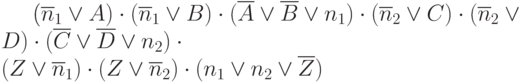
которая построена с помощью приведенных выше преобразований. Отметим, что здесь наряду с входными переменными 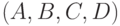 содержатся и "внутренние" переменные
содержатся и "внутренние" переменные 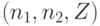 , которые ассоциированы с внутренними линиями схемы.
, которые ассоциированы с внутренними линиями схемы.
Далее перейдем, к задаче построения проверяющего теста на примере константной неисправности 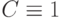 . Согласно методу различающей функции мы должны решить булево уравнение
. Согласно методу различающей функции мы должны решить булево уравнение 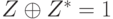 , где
, где 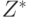 описывает поведение неисправной схемы. На рис. 21.1 представлена схема, которая реализует эту различающую функцию. Заметим, что здесь исправная и неисправная схемы содержат общую подсхему. Далее по изложенной выше методике с использованием преобразований табл. 21.1 построим КНФ для схемы рис. 21.1
описывает поведение неисправной схемы. На рис. 21.1 представлена схема, которая реализует эту различающую функцию. Заметим, что здесь исправная и неисправная схемы содержат общую подсхему. Далее по изложенной выше методике с использованием преобразований табл. 21.1 построим КНФ для схемы рис. 21.1
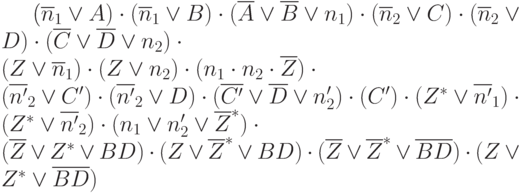
В полученной формуле первые две строки соответствуют исправной схеме, которая на рис. 21.1 выделена пунктиром. Третья строка соответствует неисправной схеме. Отметим, что здесь включено дополнительное требование на активизацию неисправности в виде терма 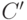 , который принимает значение "истина" при
, который принимает значение "истина" при 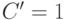 . Наконец, четвертая строка представляет элемент исключающее ИЛИ (сумма по mod2). Конечно, для маленькой схемы рис. 21.1 это выражение достаточно громоздко, но методы решения выполнимости булевых функций и высокая производительность компьютерных систем позволяют решать задачу генерации тестов для реальных больших схем. Решением, то есть проверяющим тестовым набором является множество значений входных переменных, обращающих КНФ в 1.
. Наконец, четвертая строка представляет элемент исключающее ИЛИ (сумма по mod2). Конечно, для маленькой схемы рис. 21.1 это выражение достаточно громоздко, но методы решения выполнимости булевых функций и высокая производительность компьютерных систем позволяют решать задачу генерации тестов для реальных больших схем. Решением, то есть проверяющим тестовым набором является множество значений входных переменных, обращающих КНФ в 1.
Эффективность решения выполнимости булевых функций зависит от числа термов в дизъюнктах. Известно, что в общем случае (произвольного числа термов в дизъюнктах) эта задача является NP-полной (относительно числа переменных) то есть имеет экспоненциальную сложность. Решение полиномиальной сложности имеет случай 1- и 2-выполнимости, когда число термов в любом дизъюнкте не превышает 1 или 2. Для 2-выполнимости известен эффективный алгоритм на основе метода резолюций [21.3]. Для 3-выполнимости задача уже является NP-полной. Задача с произвольным числом термов может быть сведена к 3-выполнимости[21.3]. Заметим, что для нашого примера схема содержит логические элементы, имеющие два входа. Потому, согласно табл..21.1, построенная КНФ в этом случае имеет 66,6% дизъюнктов с двумя термами. На практике 80% или даже 90% дизъюнктов имеют два терма. Поэтому часто при построении тестов используется следующий подход к решению задачи выполнимости:
- находятся значения переменных, входящие в дизъюнкты с двумя термами;
- дизъюнкты с тремя термами используются в качестве ограничений.
Подобный подход используется в [21.1,21.2] на основе линейного алгоритма для 2- выполнимости [21.4] следующим образом. Определяется массив  для 2-КНФ переменных, входящих в дизъюнкты с 2 термами. Массив определяет порядок обработки этих переменных. Используется указатель
для 2-КНФ переменных, входящих в дизъюнкты с 2 термами. Массив определяет порядок обработки этих переменных. Используется указатель  , который указывает на первую неограниченную переменную и инициализируется в 0. Переменная
, который указывает на первую неограниченную переменную и инициализируется в 0. Переменная 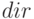 используется для хранения текущего направления обработки (прямой или обратный порядок).
В течение обработки
используется для хранения текущего направления обработки (прямой или обратный порядок).
В течение обработки 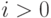 и последовательность ограниченных значений
и последовательность ограниченных значений ![V[0], V[1],…, V[i-1]](/sites/default/files/tex_cache/d3b70ee0274fe0e34dfb7fddc49f2a5d.png) представляет текущий префикс
представляет текущий префикс  . Все элементы массива
. Все элементы массива  , которые больше или равны 0 и меньше
, которые больше или равны 0 и меньше  являются ограниченными. Целью является множество двоичных значений переменных
являются ограниченными. Целью является множество двоичных значений переменных  , которые совместимы с дизъюнктами, содержащими 3 терма. При этом в случае несовместимости это желательно обнаружить как можно раньше. Укрупненный псевдокод алгоритма решения выполнимости КНФ представлен ниже на рис. 21.2.
, которые совместимы с дизъюнктами, содержащими 3 терма. При этом в случае несовместимости это желательно обнаружить как можно раньше. Укрупненный псевдокод алгоритма решения выполнимости КНФ представлен ниже на рис. 21.2.
SAT()
{
dir=0; // устанавливается прямой порядок
V=NULL; // все переменные неограниченны
i=0; // значение указателя на первую неограниченную переменную
for(;;) {
if(dir=прямой порядок) {
for(;i<размер V;i=i+1)
if(V[i] ограничена)
break;
if(i==размер V)
return(успех);
V[i-1]=0;
Выполнение импликации V[i-1];
i =i+1;
}
else { // dir=обратный порядок
if(i==0)
return(неудача);
temp=V[i]; // сохранение последнего значения
отменить импликацию V[i-1];
}
else
i=i-1;
}
if(нет нулевого дизъюнкта)
dir= прямой порядок;
else
dir= обратный порядок;
}
}
Поиск решения прекращается если:
- Найдены значения, при которых булева функция выполнима;
- Доказано, что таких значений не существует;
- Превышены ограничения по выделенным вычислительным ресурсам.
Представленный алгоритм является полным - то есть он гарантирует построение тестового набора для не избыточной неисправности в комбинационной схеме или показывает ее избыточность. Однако для ускорения поиска можно ввести в КНФ некоторые дополнительные дизъюнкты, которые позволяют сузить пространство поиска решений. Подобно структурным методам эти дизъюнкты могут отражать топологию схемы и некоторые эвристики [21.1].