|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Жадный алгоритм поиска индивидуальных масок
Покажем, что поиск одной индивидуальной маски можно свести к задаче о покрытии множества.
Пусть задана диагностическая информация в виде СПР и требуется найти индивидуальную маску для технического состояния 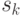 .
Для каждой возможной точки проверки
.
Для каждой возможной точки проверки 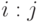 построим подмножество
построим подмножество 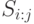 множества
множества  , в которое внесем все технические состояния, отличающиеся от состояния
, в которое внесем все технические состояния, отличающиеся от состояния 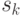 при использовании точки проверки
при использовании точки проверки 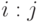 . Таким образом, получим покрытие
. Таким образом, получим покрытие

множества  . Очевидно, что минимальному подпокрытию
. Очевидно, что минимальному подпокрытию 

будет соответствовать минимальная индивидуальная маска
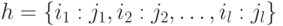
Задача нахождения минимального подпокрытия множества является 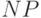 -полной.
В [1] предлагается жадный алгоритм ее решения. Идея алгоритма состоит в следующем: строим
-полной.
В [1] предлагается жадный алгоритм ее решения. Идея алгоритма состоит в следующем: строим 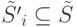 , причем
, причем 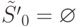 , а
, а
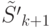 строится из
строится из
 добавлением элемента из
добавлением элемента из 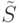 , который покрывает наибольшее количество элементов множества
, который покрывает наибольшее количество элементов множества  , непокрытых элементами из
, непокрытых элементами из
 .
Временная сложность данного алгоритма составляет
.
Временная сложность данного алгоритма составляет
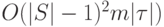 , емкостная сложность -
, емкостная сложность -  , а решение (количество элементов в искомом подпокрытии) не превосходит минимальное более чем в
, а решение (количество элементов в искомом подпокрытии) не превосходит минимальное более чем в
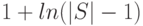 раз.
раз.
Так как поиск маски должен быть произведен для каждого технического состояния, общая временная сложность поиска всего множества индивидуальных масок составит
 . В целях обеспечения необходимого объема памяти для сохранения результатов потребуется
. В целях обеспечения необходимого объема памяти для сохранения результатов потребуется  бит, что и является оценкой емкостной сложности поиска множества индивидуальных масок.
бит, что и является оценкой емкостной сложности поиска множества индивидуальных масок.
Ниже описывается алгоритм, предложенный в [2], который улучшит приведенную временную характеристику.
При описании алгоритма будем использовать следующие обозначения. Пусть 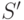 - некоторое подмножество множества технических состояний,
- некоторое подмножество множества технических состояний, 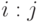 - точка проверки, а
- точка проверки, а  - высказывание, истинность которого равна нулю (ложь) или единице (истина).
Тогда через
- высказывание, истинность которого равна нулю (ложь) или единице (истина).
Тогда через 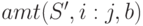 обозначим количество технических состояний из множества
обозначим количество технических состояний из множества 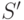 , для которых значение в точке проверки
, для которых значение в точке проверки 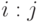 равно значению истинности
равно значению истинности  . Обозначение
. Обозначение 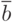 будет соответствовать логической операции отрицания высказывания
будет соответствовать логической операции отрицания высказывания  .
.
Алгоритм 2 ( Жадный алгоритм поиска множества индивидуальных масок ).
Вход: Словарь полной реакции;  - множество технических состояний.
- множество технических состояний.
Выход:  - множество индивидуальных масок.
- множество индивидуальных масок.
- Положить
 .
. - Выполненить рекурсивный алгоритм
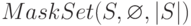 ,
описанный ниже.
,
описанный ниже. - Вернуть множество
 в качестве результата.
в качестве результата.
Алгоритм  функционирует следующим образом:
функционирует следующим образом:
- Если
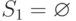 или
или
 - закончить вызов, иначе перейти к шагу 2.
- закончить вызов, иначе перейти к шагу 2.
- Найти такую точку проверки
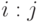 и такое значение
и такое значение 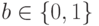 , для которых величина
достигает наибольшего значения, не превышающего
, для которых величина
достигает наибольшего значения, не превышающего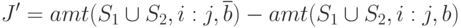
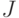 , при условии
, при условии 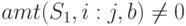 . Если такой точки проверки не найдено - завершить вызов, иначе перейти к п. 3.
. Если такой точки проверки не найдено - завершить вызов, иначе перейти к п. 3.
- Составить множества
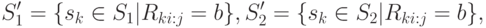
- Включить точку проверки
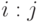 в маски
в маски 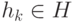 для всех технических состояний
для всех технических состояний
 .
. - Выполнить последовательно два обращения
после чего закончить вызов.
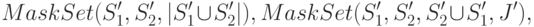
Формирование индивидуальной маски с помощью алгоритма 2 для каждого конкретного технического состояния 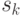 повторяет работу жадного алгоритма для поиска минимального покрытия.
Действительно, шаг 2 алгоритма
повторяет работу жадного алгоритма для поиска минимального покрытия.
Действительно, шаг 2 алгоритма  повторяет шаг исходного жадного алгоритма, на котором выбирается подмножество исходного множества, покрывающего максимальное количество элементов.
Первый рекурсивный вызов на шаге 5 алгоритма соответствует повторению алгоритма для подмножества непокрытых элементов.
повторяет шаг исходного жадного алгоритма, на котором выбирается подмножество исходного множества, покрывающего максимальное количество элементов.
Первый рекурсивный вызов на шаге 5 алгоритма соответствует повторению алгоритма для подмножества непокрытых элементов.
Суть алгоритма 2 состоит в поиске индивидуальных масок одновременно для всех технических состояний. Основная идея, направленная на ускорение данного поиска, заключается в следующем. Часто индивидуальные маски для разных технических состояний имеют одинаковые элементы.
Например, когда на шаге 2 алгоритм  находит точку проверки, по значению которой можно отличить все состояния из
находит точку проверки, по значению которой можно отличить все состояния из 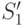 от всех состояний из
от всех состояний из 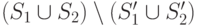 , то эта точка проверки должна быть включена во все маски, соответствующие состояниям из
, то эта точка проверки должна быть включена во все маски, соответствующие состояниям из 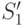 (что и делается на шаге 4).
После этого необходимо дополнить эти маски так, чтобы они отличали друг от друга состояния из
(что и делается на шаге 4).
После этого необходимо дополнить эти маски так, чтобы они отличали друг от друга состояния из 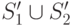 (первый рекурсивный вызов на шаге 5). Так как в результате этих действий сформированные на текущий момент маски для состояний из
(первый рекурсивный вызов на шаге 5). Так как в результате этих действий сформированные на текущий момент маски для состояний из 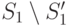 еще не могут различать эти состояния между собой и отличать их от состояний из
еще не могут различать эти состояния между собой и отличать их от состояний из 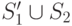 , то алгоритм повторяется с дальнейшим анализом всего множества состояний, но с учетом того, что маски для множества состояний
, то алгоритм повторяется с дальнейшим анализом всего множества состояний, но с учетом того, что маски для множества состояний 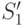 уже сформированы (второй рекурсивный вызов на шаге 5).
уже сформированы (второй рекурсивный вызов на шаге 5).
Аргумент 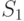 алгоритма
алгоритма  определяет набор технических состояний, для которых необходимо провести поиск индивидуальной маски. Объединение
определяет набор технических состояний, для которых необходимо провести поиск индивидуальной маски. Объединение  задает множество состояний, для которых должно быть введено отличие в масках для состояний из
задает множество состояний, для которых должно быть введено отличие в масках для состояний из 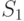 .
Аргумент
.
Аргумент 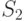 определяет множество технических состояний, для которых маски уже были найдены. Последний аргумент алгоритма
определяет множество технических состояний, для которых маски уже были найдены. Последний аргумент алгоритма  введен для упорядочения поиска точек проверки.
введен для упорядочения поиска точек проверки.
