Жадный алгоритм поиска индивидуальных масок

Следующая теорема определяет верхнюю оценку объема совокупности индивидуальных масок, возвращаемой с помощью алгоритма 2.

Теорема 1. Суммарный объем совокупности индивидуальных масок, полученной с помощью алгоритма2, не превышает величины

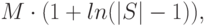
где - суммарный объем совокупности минимальных индивидуальных масок заданного СПР.

Доказательство. Обозначим через суммарное количество точек проверки, добавленное в совокупность масок в результате вызова .

Из определения алгоритма ясно, что

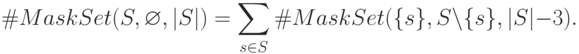
Запуск 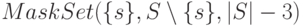возвращает индивидуальную маску для технического состояния . Работа такого запуска сводится к работе жадного алгоритма поиска минимального покрытия множества, содержащего элементов.

Известно [1], что размер покрытия множества , полученного с помощью жадного алгоритма, превосходит размер минимального покрытия не более чем в раз. Отсюда

где 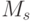- объем минимальной индивидуальной маски для технического состояния . Из последнего неравенства следует, что

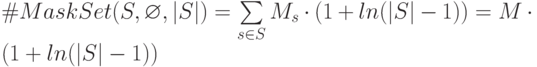
где .

В следующей теореме оценивается сложность описанного алгоритма.

Теорема 2. Временная сложность алгоритма 2 составляет . Объем дополнительной памяти, необходимой для функционирования алгоритма 2, оценивается величиной .

Доказательство. Из формулировки алгоритма 2 ясно, что его сложность равна временной сложности вызова алгоритма 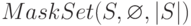. Оценим ее.

Заметим, что рекурсия по второму обращению к функции является концевой и эквивалентна итерационному процессу с параметром 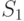(с условием окончания процесса, как только выполнится 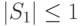). Таким образом, стоит учитывать лишь первое обращение как рекурсивный вызов.

Максимально возможная глубина рекурсии по первому обращению равна . При каждом таком рекурсивном вызове происходит уменьшение количества элементов в множестве , вследствие чего можно оценить сверху объем необходимой памяти для вызова 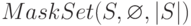величиной, кратной . Отсюда следует оценка емкостной сложности в формулировке теоремы.

Величиной той же кратности можно оценить стоимость поиска одной индивидуальной маски, а следовательно количество операций для поиска всей совокупности индивидуальных масок не превышает величины .

Ключевые термины:

Жадный алгоритм- алгоритм, основанный на принятии локально оптимальных решений на каждом этапе его работы в расчете на возможность получения глобального оптимума.

Задача о минимальном покрытии множества - классическая NP-полная задача, формулируемая следующим образом: Задано множество и семейство его подмножеств . Требуется найти такое семейство 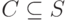,которое покрывает множество .

Краткие итоги:

В лекции описан жадный алгоритм поиска совокупности индивидуальных масок ДИ, базирующийся на сведении исходной задачи к классической задаче о минимальном покрытии множества.

Вопросы и упражнения

1. Каким образом задача о поиске совокупности индивидуальных масок может быть сведена к задаче о минимальном покрытии множества?
2. Кратко изложите идейную основу и суть алгоритма 2.
3. Какова верхняя оценка объема совокупности индивидуальных масок, получаемая по алгоритму 2?
4. Какова временная оценка сложности алгоритма 2?