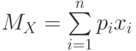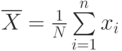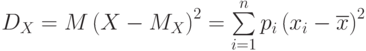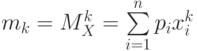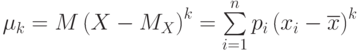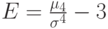Случайная величина и ее основные характеристики.
Основные определения и понятия
Расширением понятия случайных событий, состоящих в появлении некоторых числовых значений в результате эксперимента, является случайная величина Х.
Определение. Случайной называют величину, принимающую в результате эксперимента одно только значение из некоторой их совокупности и неизвестное заранее, какое именно.
Случайная величина, к примеру, представляет собой обоснованную модель описания геологических данных, учитывающую влияние различных факторов на физическое поле.
Как и результат отдельного эксперимента, точное значение случайной величины предсказать нельзя, можно лишь установить ее статистические закономерности, т.е. определить вероятности значений случайной величины. Например, измерения физических свойств горных пород являются наблюдениями соответствующих случайных величин.
Среди случайных величин, с которыми приходится встречаться геологу, можно выделить два основных типа: величины дискретные и величины непрерывные.
Определение. Дискретной случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений.
В качестве типичных примеров дискретной случайной величины могут выступать все результаты полевых работ, все результаты экспериментов, привезенные c поля образцы и пр.
Всевозможные 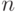 значений случайной величины образуют полную группу событий, т.е.
значений случайной величины образуют полную группу событий, т.е. 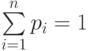 , где
, где 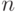 - конечное или бесконечное. Поэтому можно говорить, что случайная величина обобщает понятие случайного события.
- конечное или бесконечное. Поэтому можно говорить, что случайная величина обобщает понятие случайного события.
Пусть в результате исследований был получен следующий ряд данных по количественному составу некоторой породы: 4; 3; 1; 2; 5; 4; 2; 2; 3; 1; 5; 4; 3; 5; 5; 2; 5; 5; 6; 1. Всего было проведено 20 испытаний. Для того, чтобы с данными было удобно работать, их преобразовали: расположили полученные значения по возрастанию и подсчитали количество появления каждого из значений. В результате получили (Таблица 7.1):
Определение. Распределение данных по возрастанию называется ранжированием.
Определение. Наблюдаемое значение некоторого признака случайной величины называется вариантом.
Определение. Ряд, составленный из вариант, называется вариационным рядом.
Определение. Изменение некоторого признака случайной величины называется варьированным.
Определение. Число, показывающее сколько раз варьируется данная варианта, называется частотой и обозначается 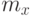 .
.
Определение. Вероятность появления данной варианты равно отношению частоты к общей сумме вариационного ряда
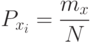 |
( 1) |
С учетом введенных определений перепишем таблицу 7.1.
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота | 3 | 4 | 3 | 3 | 6 | 1 |
| Вероятность | 3/20 | 4/20 | 3/20 | 3/20 | 6/20 | 1/20 |
При статистическом анализе экспериментальных данных главным образом используется дискретные величины. В таблице 7.3 приведены основные числовые характеристики этих величин, имеющих важное практическое значение при обработке экспериментальных данных.
| N п/п | Характеристика (параметр) случайной величины и ее обозначение | Формула для нахождения характеристики случайной величины | Примечание | ||
|---|---|---|---|---|---|
| 1 | Математическое ожидание 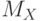
|
|
Характеризует положение случайной величины на числовой оси | ||
| 2 | Среднее значение 
|
|
Если случайная величина независимая, то 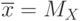
|
||
| 3 | Мода 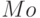
|
Это такое значение  , для которого , для которого 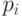 наиболь-шее наиболь-шее |
Равна наиболее часто встречающемуся значению  . Если таких значений в вариационном ряду несколько, то . Если таких значений в вариационном ряду несколько, то 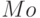 не определяется. не определяется. |
||
| 4 | Медиана 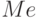
|
Если 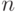 четное, то четное, то 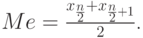 Если Если 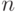 нечетное, то нечетное, то 
|
Это такое значение, которое находится в центре ранжированного ряда. | ||
| 5 | Дисперсия 
|
|
Характеризует рассеяние случайной величины вокруг среднего значения | ||
| 6 | Среднеквадратичное отклонение (стандарт) 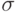
|
|
Характеризует действительное рассеяние случайной величины вокруг среднего значения. | ||
| 7 | Коэффициент вариации 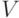
|
|
Наряду с дисперсией характеризует изменчивость случайной величины | ||
| 8 | Центрированное нормированное уклонение 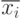
|
|
|||
| 9 | Начальный момент 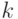 -го порядка -го порядка 
|
|
|||
| 10 | Центральный момент 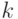 -го порядка -го порядка 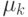
|
|
|||
| 11 | Асимметрия распределения 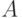
|
|
|||
| 12 | Эксцесс распределения 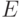
|
|
В таблице п. 8 – 12 используются для статистической обработки вариационных рядов. Об их использовании будет материал немного дальше.
В заключении заметим, что, если результат эксперимента описывается двумя и более случайными величинами, то говорят о системе случайных величин. К системе случайных величин, например, могут быть отнесены физические свойства образцов горных пород, характеристики аномальнообразующих тел, наблюдений различных полей, характеристики месторождений и т.д.