|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование при обработке опытных данных
Построение интерполяционного многочлена в явном виде
Для построения интерполяционного многочлена вида (11.2) необходимо определить его коэффициенты a0, a1, :, an, т.е. ai i=0,1,2,:,n. Количество неизвестных коэффициентов равно
n+1=N,
где
n-степень многочлена (11.2),
N-количество узловых точек табличной функции (11.1).
Для нахождения коэффициентов, используем свойство (11.3) интерполяционного многочлена (11.2). На основании этого свойства интерполяционный многочлен должен пройти через каждую узловую точку (xi, yi) таблицы (11.1), т.е.,
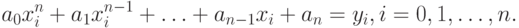 |
( 11.4) |
Подставляя в (11.4) каждую узловую точку таблицы (11.1) получаем систему линейных уравнений:
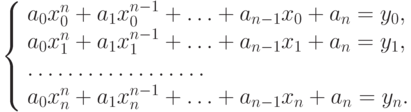 |
( 11.5) |
Неизвестными системы (11.5) являются a0, a1, a2, :, an т.е. коэффициенты многочлена (11.2). Коэффициенты при неизвестных системы (11.5) 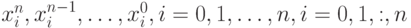 легко могут быть определены на основании данных таблицы (11.1).
легко могут быть определены на основании данных таблицы (11.1).
Интерполяция по Лагранжу
Интерполяционный многочлен может быть построен при помощи специальных интерполяционных формул Лагранжа, Ньютона, Стерлинга, Бесселя и др.
Интерполяционный многочлен по формуле Лагранжа имеет вид:
 |
( 11.6) |
Докажем, что многочлен Лагранжа является интерполяционным многочленом, проходящим через все узловые точки, т.е. в узлах интерполирования xi выполняется условие Ln(xi) = yi. Для этого будем последовательно подставлять значения координат узловых точек таблицы (11.1) в многочлен (11.6). В результате получим:
если x=x0, то Ln(x0) = y0,
если x=x1, то Ln(x1) = y1,
:::::
если x=xn, то Ln(xn) = yn.
Это достигнуто за счет того, что в числителе каждой дроби при соответствующем значении уj, j=0,1,2,:,n отсутствует сомножитель (x-xi), в котором i=j, а знаменатель каждой дроби получен заменой переменной х на соответствующее значение хj.
Таким образом, интерполяционный многочлен Лагранжа приближает заданную табличную функцию, т.е. Ln(xi) = yi и мы можем использовать его в качестве вспомогательной функции для решения задач интерполирования, т.е. 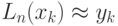 .
.
Чем больше узлов интерполирования на отрезке [x0,xn], тем точнее интерполяционный многочлен приближает заданную табличную функцию (11.1), т.е. тем точнее равенство:
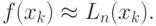
Однако с увеличением числа узлов интерполирования возрастает степень интерполяционного многочлена n и в результате значительно возрастает объем вычислительной работы. Поэтому при большом числе узлов необходимо применять ЭВМ. В этом случае удобно находить значения функции в промежуточных точках, не получая многочлен в явном виде.
При решении задачи экстраполирования функции с помощью интерполяционного многочлена вычисление значения функции за пределами отрезка [x0,xn] обычно производят не далее, чем на один шаг h, равный наименьшей величине

Программирование формулы Лагранжа
Свернем формулу Лагранжа (11.6). В результате получим
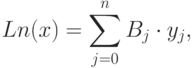
где
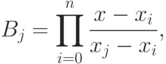
но при этом обязательно выполнение условия 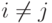 .
.
При построении алгоритма используют конструкцию из двух включенных циклов:
Внешним циклом накапливаем сумму 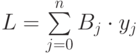 .
.
Внутренним циклом накапливаем произведение 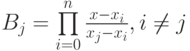 .
.
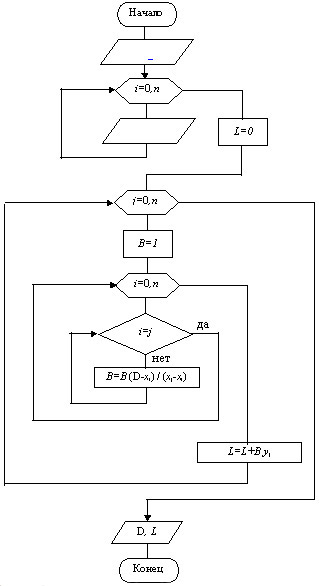
Алгоритм (рис.11.3) не предусматривает получение интерполяционного многочлена в явном виде, а сразу решает задачу интерполирования функции в заданной точке, x=D.
Обозначения в алгоритме:
n - степень интерполяционного многочлена Лагранжа (11.6), равная количеству узловых точек N минус один, т.е. n=N-1.
D - значение аргумента в точке, для которой решается задача интерполирования табличной функции (11.1).
L - значение многочлена (11.6).