Возможности нейронных сетей
Архитектура нейронных сетей
Перейдем теперь к вопросу: как можно составлять эти сети? Строго говоря, как угодно, лишь бы входы получали какие-нибудь сигналы. Но такой произвол слишком необозрим, поэтому используют несколько стандартных архитектур, из которых путем вырезания лишнего или (реже) добавления строят большинство используемых сетей.
Сначала следует договориться о том, как будет согласована работа различных нейронов во времени. Как только в системе возникает более одного элемента, встает вопрос о синхронности функционирования. Для привычных нам всем программных имитаторов нейронных сетей на цифровых ЭВМ такого вопроса нет только из-за свойств основного компьютера, на котором реализуются нейронные сети. Для других способов реализации такой вопрос весьма важен. Все же здесь и далее рассматриваются только нейронные сети, синхронно функционирующие в дискретные моменты времени: все нейроны срабатывают "разом".
В зоопарке нейронных сетей можно выделить две базовых архитектуры - слоистые и полносвязные сети.
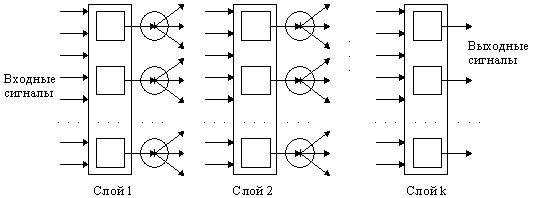
Слоистые сети: нейроны расположены в несколько слоев (рис. 1.7). Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее срабатывает второй слой и т.д. до k -го слоя, который выдает выходные сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал i -го слоя подается на вход всех нейронов i+1 -го. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал. Особое распространение получили трехслойные сети, в которых каждый слой имеет свое наименование: первый - входной, второй - скрытый, третий - выходной.
Полносвязные сети: каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам.
Элементы слоистых и полносвязных сетей могут выбираться по-разному. Существует, впрочем, стандартный выбор - нейрон с адаптивным неоднородным линейным сумматором на входе (рис. 1.5).
Для полносвязной сети входной сумматор нейрона фактически распадается на два: первый вычисляет линейную функцию от входных сигналов сети, второй - линейную функцию от выходных сигналов других нейронов, полученных на предыдущем шаге.
Функция активации нейронов (характеристическая функция) 
- нелинейный преобразователь, преобразующий выходной сигнал сумматора (см. рис. 1.5) - может быть одной и той же для всех нейронов сети. В этом случае сеть называют однородной (гомогенной) . Если же зависит еще от одного или нескольких параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной) .
Составление сети из нейронов стандартного вида (рис. 1.5) не является обязательным. Слоистая или полносвязная архитектуры не налагают существенных ограничений на участвующие в них элементы. Единственное жесткое требование, предъявляемое архитектурой к элементам сети, это соответствие размерности вектора входных сигналов элемента (она определяется архитектурой) числу его входов.
Если полносвязная сеть функционирует до получения ответа заданное число тактов k, то ее можно представить как частный случай k -слойной сети, все слои которой одинаковы и каждый из них соответствует такту функционирования полносвязной сети.
Существенное различие между полносвязной и слоистой сетями возникает тогда, когда число тактов функционирования заранее не ограничено - слоистая сеть так работать не может.
Существуют ли функции многих переменных ?
Вопрос, вынесенный в заголовок раздела, естественно возникает при изучении возможностей нейронных сетей. Из схем предыдущих разделов видно, что нейронные сети вычисляют линейные функции, нелинейные функции одного переменного, а также всевозможные суперпозиции - функции от функций, получаемые при каскадном соединении сетей. Что можно получить, используя только такие операции? Какие функции удастся вычислить точно, а какие функции можно сколь угодно точно аппроксимировать с помощью нейронных сетей? Чтобы изучить возможности нейронных сетей, нужно ответить на эти вопросы.
Заданный вопрос имеет очень большую историю и заведомо старше, чем исследования искусственных нейронных сетей.
Какие функции может вычислять человек? Если мы умеем складывать и умножать числа, то мы можем точно вычислять многочлены и рациональные функции (отношения многочленов) с рациональными коэффициентами от рациональных же аргументов.
Можно, однако, задавать функции с помощью уравнений. Если считать решения нескольких простых уравнений известными, то класс вычисляемых функций расширится - решения некоторых более общих уравнений удастся выразить через эти, более простые функции.
Классический пример: если использовать радикалы - решения уравнений xn=a, то можно явно получить решения произвольных уравнений 2 -й, 3 -й и 4 -й степеней. Так, функция 3 -х переменных a, b, c - решение уравнения ax2+bx+c=0 - может быть точно выражена с помощью сложения, умножения, деления и функции одного переменного - квадратного корня.
Вопрос: можно ли представить решение любого алгебраического уравнения с помощью радикалов, был окончательно и отрицательно решен Абелем и Галуа - уже уравнения 5 -й степени неразрешимы в радикалах.
Все же можно подбирать другие простые функции небольшого числа переменных - сложнее, чем радикалы, но проще, чем общие решения уравнений высоких степеней. Удастся ли с помощью этих функций построить решение любого уравнения? Вопрос был настолько важен, что Гильберт в списке своих проблем, которые, по его мнению, должны были определять развитие математики XX века, под номером 13 поместил следующую задачу:
Представляется ли корень уравнения
x7+ax3+bx2+cx+1=0
(как функция коэффициентов) суперпозицией каких-либо непрерывных функций двух переменных?
Для уравнений 5 -й и 6 -й степени такое представление возможно не только с помощью непрерывных, но даже аналитических функций.
Оказалось полезным абстрагироваться от уравнений и поставить общий вопрос: можно ли произвольную непрерывную функцию n переменных получить с помощью операций сложения, умножения и суперпозиции из непрерывных функций двух переменных? Ответ оказался положительным! В серии работ [1.1, 1.2, 1.3] А.Н.Колмогоров, затем В.И.Арнольд и вновь А.Н.Колмогоров решили эту проблему: можно получить любую непрерывную функцию n переменных с помощью операций сложения, умножения и суперпозиции из непрерывных функций одного переменного.
Последняя теорема А.Н.Колмогорова [1.3] из этой серии настолько проста и изящна, что мы чуть позже приведем ее целиком. А пока - несколько замечаний о условиях теоремы.
От условия непрерывности можно отказаться - тогда получится довольно тривиальный результат связанный, по существу, с равномощностью отрезка и куба любой размерности. Условие непрерывности нельзя значительно усилить: существуют аналитические функции многих переменных, которые не допускают представления с помощью суперпозиции аналитических функций двух переменных. Более того, все l раз непрерывно дифференцируемые функции трех переменных нельзя представить в виде суперпозиций функций двух переменных, каждая из которых дифференцируема [2l/3] раз и все частные производные которых порядка [2l/3] удовлетворяют условию Липшица (выражение [2l/3] означает целую часть числа 2l/3 ). Это доказано А.Г,Витушкиным [1.4].