Решение задач нейронными сетями

Решение задач нейронными сетями

Вычислительный центр СО РАН в г. Красноярске

А.Н.Горбань

Нейронные сети могут все. Но точно также "все" могут машины Тьюринга, интерполяционные многочлены, схемы Поста, ряды Фурье, рекурсивные функции, дизъюнктивные нормальные формы, сети Петри. В предыдущей лекции было показано, что с помощью нейронных сетей можно сколь угодно точно аппроксимировать любую непрерывную функцию и имитировать любой непрерывный автомат. Это и слишком много - никому не нужен столь широкий класс функций, и слишком мало, так как далеко не все важные задачи ставятся как задачи аппроксимации.

Другое дело, что в конечном итоге решение практически любой задачи можно описать, как построение некоторой функции, перерабатывающей исходные данные в результат, но такое очень общее описание не дает никакой информации о способе построения этой функции. Мало иметь универсальные способности - надо для каждого класса задач указать, как применять эти способности. Именно здесь, при рассмотрении методов настройки нейронных сетей для решения задач должны выявиться реальные рамки их применимости. Конечно, такие реальные рамки изменяются со временем из-за открытия новых методов и решений.

В данной лекции описано несколько базовых задач для нейронных сетей и основных или исторически первых методов настройки сетей для их решения:

1. Классификация (с учителем) (персептрон Розенблатта [2.1, 2.2, 2.3]).
2. Ассоциативная память (сети Хопфилда [2.4, 2.5, 2.6, 2.7]).
3. Решение систем линейных уравнений (сети Хопфилда [2.8]).
4. Восстановление пробелов в данных (сети Хопфилда).
5. Кластер-анализ и классификация (без учителя) (сети Кохонена [2.9, 2.10, 2.11, 2.12]).

Начнем мы, однако, не с сетей, а с систем, состоящих из одного элемента.

Настройка одноэлементных систем для решения задач

Даже системы из одного адаптивного сумматора находят очень широкое применение. Вычисление линейных функций необходимо во многих задачах. Вот неполный перечень "специальностей" адаптивного сумматора:

1. Линейная регрессия и восстановление простейших закономерностей [2.13, 2.14];
2. Линейная фильтрация и адаптивная обработка сигналов [2.15];
3. Линейное разделение классов и простейшие задачи распознавания образов [2.16, 2.17, 2.18].

Задача линейной регрессии состоит в поиске наилучшего линейного приближения функции, заданной конечным набором значений: дана выборка значений вектора аргументов x¹, ..., x^m, заданы значения функции F в этих точках: F(xⁱ)=f_i, требуется найти линейную (неоднородную) функцию 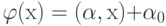, ближайшую к F. Чтобы однозначно поставить задачу, необходимо доопределить, что значит "ближайшую". Наиболее популярен метод наименьших квадратов, согласно которому ищется из условия

( 1)

Необходимо особенно подчеркнуть, что метод наименьших квадратов не является ни единственным, ни наилучшим во всех отношениях способом доопределения задачи регрессии. Его главное достоинство - квадратичность минимизируемого критерия и линейность получаемых уравнений на коэффициенты .

Явные формулы линейной регрессии легко получить, минимизируя квадратичный критерий качества регрессии. Обозначим

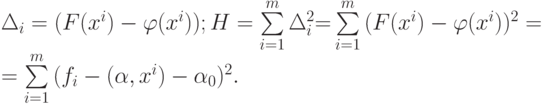
Найдем производные минимизируемой функции H по настраиваемым параметрам:

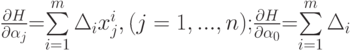
где xⁱ_j - j -я координата вектора xⁱ.

Приравнивая частные производные H нулю, получаем уравнения, из которых легко найти все 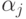( j=0,...,n ). Решение удобно записать в общем виде, если для всех i=1,...,m обозначить 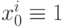и рассматривать n +1 -мерные векторы данных xⁱ и коэффициентов . Тогда

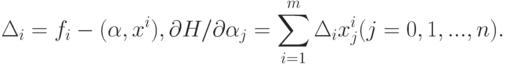
Обозначим p n +1 -мерный вектор с координатами 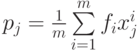; Q - матрицу размером с элементами .

В новых обозначениях решение задачи линейной регрессии имеет вид:

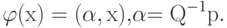( 2)