Решение задач нейронными сетями

Задача четкого разделения двух классов по обучающей выборке ставится так: имеется два набора векторов x¹, ..., x^m и y¹,...,y^m. Заранее известно, что xⁱ относится к первому классу, а yⁱ - ко второму. Требуется построить решающее правило, то есть определить такую функцию f(x), что при f(x)>0 вектор x относится к первому классу, а при f(x)<0 - ко второму.

Координаты классифицируемых векторов представляют собой значения некоторых признаков (свойств) исследуемых объектов.

Эта задача возникает во многих случаях: при диагностике болезней и определении неисправностей машин по косвенным признакам, при распознавании изображений и сигналов и т.п.

Строго говоря, классифицируются не векторы свойств, а объекты, которые обладают этими свойствами. Это замечание становится важным в тех случаях, когда возникают затруднения с построением решающего правила - например тогда, когда встречаются принадлежащие к разным классам объекты, имеющие одинаковые признаки. В этих случаях возможно несколько решений:

1. искать дополнительные признаки, позволяющие разделить классы;
2. примириться с неизбежностью ошибок, назначить за каждый тип ошибок свой штраф ( c₁₂ - штраф за то, что объект первого класса отнесен ко второму, c₂₁ - за то, что объект второго класса отнесен к первому) и строить разделяющее правило так, чтобы минимизировать математическое ожидание штрафа;
3. перейти к нечеткому разделению классов - строить так называемые "функции принадлежности" f₁(x) и f₂(x) - f_i(x) оценивает степень уверенности при отнесении объекта к i -му классу ( i=1,2 ), для одного и того же x может быть так, что и f₁(x)>0, и f₂(x)>0.

Линейное разделение классов состоит в построении линейного решающего правила - то есть такого вектора и числа 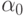(называемого порогом), что при относится к первому классу, а при - ко второму.

Поиск такого решающего правила можно рассматривать как разделение классов в проекции на прямую. Вектор задает прямую, на которую ортогонально проектируются все точки, а число 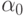- точку на этой прямой, отделяющую первый класс от второго.

Простейший и подчас очень удобный выбор состоит в проектировании на прямую, соединяющую центры масс выборок. Центр масс вычисляется в предположении, что массы всех точек одинаковы и равны 1. Это соответствует заданию в виде

Во многих случаях удобнее иметь дело с векторами единичной длины. Нормируя , получаем:

Выбор 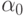может производиться из различных соображений. Простейший вариант - посередине между центрами масс выборок:

Более тонкие способы построения границы раздела классов 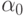учитывают различные вероятности появления объектов разных классов, и оценки плотности распределения точек классов на прямой. Чем меньше вероятность появления данного класса, тем более граница раздела приближается к центру тяжести соответствующей выборки.

Можно для каждого класса построить приближенную плотность вероятностей распределения проекций его точек на прямую (это намного проще, чем для многомерного распределения) и выбирать 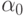, минимизируя вероятность ошибки. Пусть решающее правило имеет вид: при > 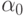x относится к первому классу, а при < 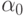- ко второму. В таком случае вероятность ошибки будет равна

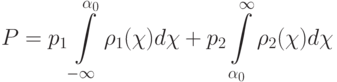
где p₁, p₂ - априорные вероятности принадлежности объекта соответствующему классу, , - плотности вероятности для распределения проекций точек x в каждом классе.

Приравняв нулю производную вероятности ошибки по 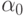, получим: число 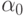, доставляющее минимум вероятности ошибки, является корнем уравнения:

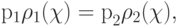( 7)

либо (если у этого уравнения нет решений) оптимальным является правило, относящее все объекты к одному из классов.

Если принять гипотезу о нормальности распределений:

то для определения 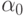получим: