Быстрое дифференцирование, двойственность и обратное распространение ошибки
Вычислительный центр СО РАН в г. Красноярске
В этой лекции излагается материал, значение которого для вычислительной математики и всего того, что по-английски именуют "computer sciences", выходит далеко за пределы нейроинформатики. Со временем он безусловно будет включен в программы университетских курсов математического анализа.
Обсудим одну "очевидную" догму, без разрушения которой было бы невозможно эффективное обучение нейронных сетей. Пусть вычислительные затраты (оцениваемые временем, затраченным некоторым универсальным вычислительным устройством) на вычисление одного значения функции n переменных H(x1,...,xn) примерно равны T. Сколько времени потребуется тому же устройству на вычисление gradH (при разумном составлении программы)? Большинство математиков с университетским дипломом ответит:
TgradH ~ nTH. (1)
Это неверно! Правильный ответ:
TgradH~ CTH . (2)
где C - константа, не зависящая от размерности n (в большинстве случаев C~3 ).
Для всех функций многих переменных, встречающихся на практике, необходимые вычислительные затраты на поиск их градиента всего лишь в два-три раза превосходят затраты на вычисление одного значения функции. Это удивительно - ведь координатами вектора градиента служат n частных производных, а затраты на вычисление одной такой производной в общем случае примерно такие же, как и на вычисление значения функции. Почему же вычисление всех их вместе дешевле, чем по-отдельности?
"Чудо" объясняется довольно просто: нужно рационально организовать вычисление производных сложной функции многих переменных, избегая дублирования. Для этого необходимо подробно представить само вычисление функции, чтобы потом иметь дело не с "черным ящиком", преобразующим вектор аргументов в значение функции, а с детально описанным графом вычислений.
Поиск gradH удобно представить как некоторый двойственный процесс над структурой вычисления H. Промежуточные результаты, появляющиеся при вычислении градиента, являются ни чем иным, как множителями Лагранжа. Оказывается, что если представить H как сложную функцию, являющуюся суперпозицией функций малого числа переменных (а по-другому вычислять функции многих переменных мы не умеем), и аккуратно воспользоваться правилом дифференцирования сложной функции, не производя по дороге лишних вычислений и сохраняя полезные промежуточные результаты, то вычисление всей совокупности 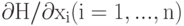 немногим сложнее, чем одной из этих функций - они все собраны из одинаковых блоков.
немногим сложнее, чем одной из этих функций - они все собраны из одинаковых блоков.
Я не знаю, кто все это придумал первым. В нейроинформатике споры о приоритете ведутся до сих пор. Конец переоткрытиям положили две работы 1986 г.: Румельхарта, Хинтона и Вильямса [3.1, 3.2] и Барцева и Охонина [3.3]. Однако первые публикации относятся к 70-м и даже 60-м годам нашего столетия. По мнению В.А.Охонина, Лагранж и Лежандр также вправе претендовать на авторство метода.
Обучение нейронных сетей как минимизация функции ошибки
Построение обучения как оптимизации дает нам универсальный метод создания нейронных сетей для решения задач. Если сформулировать требования к нейронной сети, как задачу минимизации некоторой функции - оценки, зависящей от части сигналов (входных, выходных, ...) и от параметров сети, то обучение можно рассматривать как оптимизацию и строить соответствующие алгоритмы, программное обеспечение и, наконец, устройства (hardware). Функция оценки обычно довольно просто (явно) зависит от части сигналов - входных и выходных. Ее зависимость от настраиваемых параметров сети может быть сложнее и включать как явные компоненты (слагаемые, сомножители,...), так и неявные - через сигналы (сигналы, очевидно, зависят от параметров, а функция оценки - от сигналов).
За пределами задач, в которых нейронные сети формируются по явным правилам (сети Хопфилда, проективные сети, минимизация аналитически заданных функций и т.п.) нам неизвестны случаи, когда требования к нейронной сети нельзя было бы представить в форме минимизации функции оценки. Не следует путать такую постановку задачи и ее весьма частный случай - "обучение с учителем". Уже метод динамических ядер, описанный в "Решение задач нейронными сетями" , показывает, каким образом обучение без учителя в задачах классификации может быть описано как минимизация целевой функции, оценивающей качество разбиения на классы.
Если для решения задачи не удается явным образом сформировать сеть, то проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы ("как правило") связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки.
Минимизация оценки - сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС - от 100 до 1000000 ), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов, извилистых оврагов и т.п.
Наконец, даже для того, чтобы воспользоваться простейшими методами гладкой оптимизации, нужно вычислять градиент функции оценки. Здесь мы сталкиваемся с одной "очевидной" догмой, без разрушения которой было бы невозможно эффективное обучение нейронных сетей.
Граф вычисления сложной функции
Сложная функция задается с помощью суперпозиции некоторого набора "простых". Простые функции принадлежат исходно задаваемому конечному множеству F. Формально они выделены только принадлежностью к множеству F - никаких обязательных иных отличий этих функций от всех прочих в общем случае не предполагается.
В этом разделе мы изучим способы задания сложных функций, то есть формулы и соответствующие им графы. Свойства самих функций нас сейчас не интересуют (будем рассматривать ноты, а не слушать музыку).
Теория выражений, определяющих сложные функции, является простейшим разделом математической логики, в которой сами эти выражения называются термами [3.4].
Термы - это правильно построенные выражения в некотором формальном языке. Чтобы задать такой язык, необходимо определить его алфавит. Он состоит из трех множеств символов:
- C - множество символов, обозначающих константы;
- V - множество символов, обозначающих переменные;
-
F - множество функциональных символов,
 , где
, где 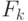 - множество символов для обозначения функций k переменных.
- множество символов для обозначения функций k переменных.
Вводя различные множества символов, мы постоянно обращаемся к их интерпретации ("... символы, обозначающие..."). Строго говоря, это не нужно - можно (а с чисто формальной точки зрения - и должно) описать все правила действия с символами, не прибегая к их интерпретации, однако ее использование позволяет сократить изложение формальных правил за счет обращения к имеющемуся содержательному опыту.
Термы определяются индуктивно:
- любой символ из
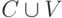 есть терм;
есть терм; - если
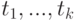 - термы и
- термы и 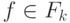 , то
, то 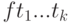 - терм.
- терм.
Множество термов T представляет собой объединение:
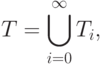
где  ,
,
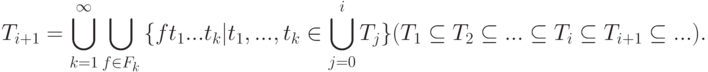
Удобно разбить T на непересекающиеся множества - слои 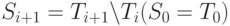 . Элементы
. Элементы 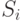 будем называть термами глубины i или i -слойными термами. Множеству
будем называть термами глубины i или i -слойными термами. Множеству 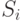 принадлежат выражения, обозначающие те функции от термов предыдущих слоев
принадлежат выражения, обозначающие те функции от термов предыдущих слоев 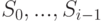 , которые сами им не принадлежат1Трудно удержаться от вольности речи - обращения к формально еще не введенной, но совершенно очевидной интерпретации ("... обозначающие...").
.
, которые сами им не принадлежат1Трудно удержаться от вольности речи - обращения к формально еще не введенной, но совершенно очевидной интерпретации ("... обозначающие...").
.
Для оперирования с термами очень полезны две теоремы [3.4].
