Быстрое дифференцирование, двойственность и обратное распространение ошибки

Оптимизационное обучение нейронных сетей

Когда можно представить обучение нейронных сетей как задачу оптимизации? В тех случаях, когда удается оценить работу сети. Это означает, что можно указать, хорошо или плохо сеть решает поставленные ей задачи и оценить это "хорошо или плохо" количественно. Строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) - от всех ее параметров. Простейший и самый распространенный пример оценки - сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

где 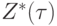- требуемое значение выходного сигнала.

Другой пример оценки - качество классификации в сетях Кохонена. В этом случае ответы заранее неизвестны, но качество работы сети оценить можно.

Устройство, вычисляющее оценку, надстраивается над нейронной сетью и градиент оценки может быть вычислен с использованием описанного принципа двойственности.

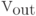В тех случаях, когда оценка является суммой квадратов ошибок, значения независимых переменных двойственного функционирования для вершин выходного слоя при вычислении градиента H устанавливаются равными

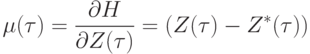( 19)

на вход при обратном функционировании поступают ошибки выходных сигналов! Это обстоятельство настолько впечатлило исследователей, что они назвали метод вычисления градиента оценки методом обратного распространения ошибок. Впрочем, после формулы Уидроу, описанной в "Решение задач нейронными сетями" , формула (19) должна быть очевидной.

Для обучения используется оценка, усредненная по примерам с известным ответом.

Предлагается рассматривать обучение нейронных сетей как задачу оптимизации. Это означает, что весь мощный арсенал методов оптимизации может быть испытан для обучения. Так и видится: нейрокомпьютеры наискорейшего спуска, нейрокомпьютеры Ньютона, Флетчера и т.п. - по названию метода нелинейной оптимизации.

Существует, однако, ряд специфических ограничений. Они связаны с огромной размерностью задачи обучения. Число параметров может достигать 10⁸ - и даже более. Уже в простейших программных имитаторах на персональных компьютерах подбирается 10³ - 10⁴ параметров.

Из-за высокой размерности возникает два требования к алгоритму:

1. Ограничение по памяти. Пусть n - число параметров. Если алгоритм требует затрат памяти порядка n², то он вряд ли применим для обучения. Вообще говоря, желательно иметь алгоритмы, которые требуют затрат памяти порядка Kn, K=const.
2. Возможность параллельного выполнения наиболее трудоемких этапов алгоритма и желательно - нейронной сетью. Если какой-либо особо привлекательный алгоритм требует память порядка n², то его все же можно использовать, если с помощью анализа чувствительности и, возможно, контрастирования сократить число обучаемых параметров до разумных пределов.

Еще два обстоятельства связаны с нейрокомпьютерной спецификой.

1. Обученный нейрокомпьютер должен с приемлемой точностью решать все тестовые задачи (или, быть может, почти все с очень малой частью исключений). Поэтому задача обучения становится по существу многокритериальной задачей оптимизации: надо найти точку общего минимума большого числа функций. Обучение нейрокомпьютера исходит из гипотезы о существовании такой точки. Основания гипотезы - очень большое число переменных и сходство между функциями. Само понятие "сходство" здесь трудно формализовать, но опыт показывает что предположение о существовании общего минимума или, точнее, точек, где значения всех оценок мало отличаются от минимальных, часто оправдывается.
2. Обученный нейрокомпьютер должен иметь возможность приобретать новые навыки без утраты старых. Возможно более слабое требование: новые навыки могут сопровождаться потерей точности в старых, но эта потеря не должна быть особо существенной, а качественные изменения должны быть исключены. Это означает, что в достаточно большой окрестности найденной точки общего минимума оценок значения этих функций незначительно отличаются от минимальных. Мало того, что должна быть найдена точка общего минимума, так она еще должна лежать в достаточно широкой низменности, где значения всех минимизируемых функций близки к минимуму. Для решения этой задачи нужны специальные средства.

Итак, имеем четыре специфических ограничения, выделяющих обучение нейрокомпьютера из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном - это просто задача оптимизации и многие классические и современные методы достаточно естественно ложатся на структуру нейронной сети.

Заметим, кстати, что если вести оптимизацию (минимизацию ошибки), меняя параметры сети, то в результате получим решение задачи аппроксимации. Если же ведется минимизация целевой некоторой функции и ищутся соответствующие значения переменных, то в результате решаем задачу оптимизации (хотя формально это одна и та же математическая задача и разделение на параметры и переменные определяется логикой предметной области, а с формальной точки зрения разница практически отсутствует).

Значительное число публикаций по методам обучения нейронных сетей посвящено переносу классических алгоритмов оптимизации (см., например, [3.7, 3.8]) на нейронные сети или поиску новых редакций этих методов, более соответствующих описанным ограничениям - таких, например, как метод виртуальных частиц [3.5, 3.6]. Существуют обширные обзоры и курсы, посвященные обучению нейронных сетей (например, [3.9, 3.10]). Не будем здесь останавливаться на обзоре этих работ - если найден градиент, то остальное приложится.

Работа над лекцией была поддержана Красноярским краевым фондом науки, грант 6F0124.