НОУ ИНТУИТ | Нейроинформатика. Лекция 3: Быстрое дифференцирование, двойственность и обратное распространение ошибки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1638 / 246 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист

|

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Двойственность по Лежандру и смысл двойственных переменных

Просматривая текст предыдущих разделов, я убедился, что подробное изложение и элементы стиля математической логики могут даже очевидное сделать сложным. В данном разделе описывается связь двойственного функционирования сетей автоматов с преобразованием Лежандра и неопределенными множителями Лагранжа. Это изложение ориентировано на читателя, знакомившегося с лагранжевым и гамильтоновым формализмами и их связью (в классической механике или вариационном исчислении). Фактически на двух страницах будет заново изложен весь предыдущий материал лекции.

Переменные обратного функционирования $\mu$ появляются как вспомогательные при вычислении производных сложной функции. Переменные такого типа появляются не случайно. Они постоянно возникают в задачах оптимизации и являются множителями Лагранжа.

Мы вводим 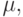$\mu,$ исходя из правил дифференцирования сложной функции. Возможен другой путь, связанный с переходом от функции Лагранжа к функции Гамильтона. Изложим его и параллельно получим ряд дальнейших обобщений. Для всех сетей автоматов, встречавшихся нам в предыдущих разделах и лекциях, можно выделить три группы переменных:

внешние входные сигналы x...,
переменные функционирования - значения на выходах всех элементов сети f...,
переменные обучения a...

(многоточиями заменяются различные наборы индексов).

Объединим их в две группы - вычисляемые величины y... - значения f... и задаваемые - b... (включая a... и x...). Упростим индексацию, перенумеровав f и b натуральными числами: f₁,...,f_N; b₁,...,b_M.

Пусть функционирование системы задается набором из N уравнений

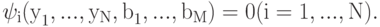$\psi_{\rm{i}}{\rm{(y}}_1 ,...,{\rm{y}}_{\rm{N}}{\rm{,b}}_1 ,...,{\rm{b}}_{\rm{M}}{\rm{) = 0 (i = 1}},...,{\rm{N)}}.$

( 13)

Для послойного вычисления сложных функций вычисляемые переменные - это значения вершин для всех слоев, кроме нулевого, задаваемые переменные - это значения вершин первого слоя (константы и значения переменных), а уравнения функционирования имеют простейший вид (4), для которого

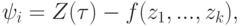
$\psi_i = Z(\tau ) - f(z_1 ,...,z_k ),$

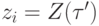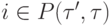где $z_i = Z(\tau ')$ при $i \in P(\tau ',\tau )$ .

Предполагается, что система уравнений (13) задает способ вычисления y_i.

Пусть имеется функция (лагранжиан) H(y₁,...,y_N,b₁,...,b_M). Эта функция зависит от b и явно, и неявно - через переменные функционирования y. Если представить, что уравнения (13) разрешены относительно всех y ( y=y(b) ), то H можно представить как функцию от b:

H=H₁ (b)=H(y₁ (b),...,y_N (b),b). 		(14)

где b - вектор с компонентами b_i.

Для задачи обучения требуется найти производные 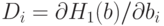$D_{i} =\partial H_{1}(b)/\partial b_{i}$ . Непосредственно и явно это сделать трудно.

Поступим по-другому. Введем новые переменные 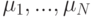$\mu _{1},...,\mu _{N}$ (множители Лагранжа) и производящую функцию W:

$W(y,b,\mu ) = H(y,b) + \sum\limits_{i = 1}^{N\mu }{\mu_i \psi_i (y,b).}$

В функции W аргументы y, b и $\mu$ - независимые переменные.

Уравнения (13) можно записать как

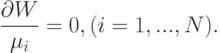$\frac{{\partial W}}{{\mu_i }}= 0,{\rm{(}}i = 1,...,N).$

( 15)

Заметим, что для тех y, b, которые удовлетворяют уравнениям (13), при любых $\mu$

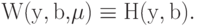${\rm{W(y}}{\rm{,b}}{\rm{,}}\mu {\rm{)}}\equiv {\rm{H(y}}{\rm{,b)}}.$

( 16)

Это означает, что для истинных значений переменных функционирования y при данных b функция 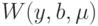$W(y,b, \mu)$ совпадает с исследуемой функцией H.

Попытаемся подобрать такую зависимость 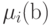$\mu_i {\rm{(b)}}$ , чтобы, используя (16), получить для 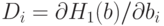$D_{i} =\partial H_{1}(b)/\partial b_{i}$ наиболее простые выражения. На многообразии решений (15)

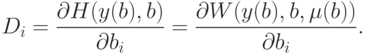
$D_i = \frac{{\partial H(y(b),b)}}{{\partial b_i }}= \frac{{\partial W(y(b),b,\mu (b))}}{{\partial b_i }}.$

Поэтому

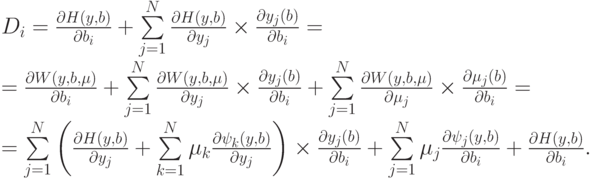$\begin{array}{l} D_i = \frac{{\partial H(y,b)}}{{\partial b_i }}+ \sum\limits_{j = 1}^N {\frac{{\partial H(y,b)}}{{\partial y_j }}\times \frac{{\partial y_j (b)}}{{\partial b_i }}}= \\ = \frac{{\partial W(y,b,\mu )}}{{\partial b_i }}+ \sum\limits_{j = 1}^N {\frac{{\partial W(y,b,\mu )}}{{\partial y_j }}\times \frac{{\partial y_j (b)}}{{\partial b_i }}}+ \sum\limits_{j = 1}^N {\frac{{\partial W(y,b,\mu )}}{{\partial \mu_j }}\times \frac{{\partial \mu_j (b)}}{{\partial b_i }}}= \\ = \sum\limits_{j = 1}^N {\left( {\frac{{\partial H(y,b)}}{{\partial y_j }}+ \sum\limits_{k = 1}^N {\mu_k \frac{{\partial \psi_k (y,b)}}{{\partial y_j }}}}\right) \times \frac{{\partial y_j (b)}}{{\partial b_i }}+ \sum\limits_{j = 1}^N {\mu_j \frac{{\partial \psi_j (y,b)}}{{\partial b_i }}}}+ \frac{{\partial H(y,b)}}{{\partial b_i }}{\rm{.}}\\ \end{array}$

( 17)

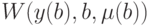Мы всюду различаем функцию H(y,b), где y и b - независимые переменные, и функцию только от переменных b H(y(b),b), где y(b) определены из уравнений (13). Аналогичное различение принимается для функций $W(y,b,\mu )$ и $W(y(b),b,\mu (b))$ .

Произвол в определении 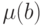$\mu (b)$ надо использовать наилучшим образом - все равно от него придется избавляться, доопределяя зависимости. Если выбрать такие 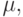$\mu,$ что слагаемые в первой сумме последней строки выражения (17) обратятся в нуль, то формула для D_i резко упростится. Положим поэтому

${\frac{\partial H(y,b)}{\partial y_j }}{\rm{ + }} {\sum\limits_{k = 1}^N {\mu_k \frac{{\partial \psi_k (y,b)}}{{\partial y_j }}}= 0}.$

( 18)

Это - система уравнений для определения 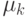$\mu _{k}$ ( k=1,...,N ). Если $\mu$ определены согласно (18), то

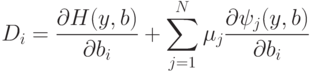
$D_i = \frac{{\partial H(y,b)}}{{\partial b_i }}+ \sum\limits_{j = 1}^N {\mu_j \frac{{\partial \psi_j (y,b)}}{{\partial b_i }}}$

это - в точности те выражения, которые использовались при поиске производных сложных функций. В наших вычислениях мы пользовались явным описанием функционирования. Метод множителей Лагранжа допускает и менее явные описания сетей.

В математическом фольклоре бытует такой тезис: сложная задача оптимизации может быть решена только при эффективном использовании двойственности. Методы быстрого дифференцирования являются яркой иллюстрацией этого тезиса.

Дальше >>

Авторизоваться

Нейроинформатика

Быстрое дифференцирование, двойственность и обратное распространение ошибки

Двойственность по Лежандру и смысл двойственных переменных

Вопросы и ответы