Быстрое дифференцирование, двойственность и обратное распространение ошибки
Теорема 3. Существует и единственен терм t, для которого 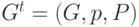 .
.
Доказательство проводится в два этапа. Сначала в G устанавливается послойная структура: строится разбиение множества вершин G: 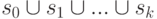 . Множество
. Множество  состоит из тех вершин, к которым не ведет ни одного ребра - из-за отсутствия ориентированных циклов такие вершины существуют. Множество
состоит из тех вершин, к которым не ведет ни одного ребра - из-за отсутствия ориентированных циклов такие вершины существуют. Множество 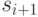 состоит из тех вершин, к которым ведут ребра только из элементов
состоит из тех вершин, к которым ведут ребра только из элементов  . Последний непустой элемент в последовательности
. Последний непустой элемент в последовательности 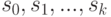 состоит из одной вершины
состоит из одной вершины 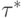 , все предшествующие элементы этой последовательности непусты, а объединение всех
, все предшествующие элементы этой последовательности непусты, а объединение всех 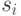 содержит все вершины G.
содержит все вершины G.
Доказательство основного утверждения теоремы проводится индукцией по числу слоев k.
Интерпретация сопоставляет терму сложную функцию. Она строится так. Задается некоторое множество D - область интерпретации. Каждой константе с, входящей в интерпретируемый терм t, сопоставляется элемент из D ( 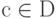 ), каждому k -местному функциональному символу f, входящему в t, сопоставляется функция k переменных
), каждому k -местному функциональному символу f, входящему в t, сопоставляется функция k переменных 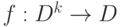 (мы сохраняем одинаковое обозначение для символов и их интерпретации, это вполне соответствует интуиции и не должно приводить к путанице). Каждой переменной, входящей в интерпретируемый терм t, сопоставляется переменная, пробегающая D. В результате терму t сопоставляется функция n переменных
(мы сохраняем одинаковое обозначение для символов и их интерпретации, это вполне соответствует интуиции и не должно приводить к путанице). Каждой переменной, входящей в интерпретируемый терм t, сопоставляется переменная, пробегающая D. В результате терму t сопоставляется функция n переменных  , где n - число различных символов переменных, входящих в t.
Эта "сложная" функция получается суперпозицией "простых" функций, соответствующих функциональным символам.
, где n - число различных символов переменных, входящих в t.
Эта "сложная" функция получается суперпозицией "простых" функций, соответствующих функциональным символам.
Если  , то есть терм является константой или переменной, то вместо сложной функции
, то есть терм является константой или переменной, то вместо сложной функции 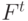 получаем константу или тождественную функцию id, переводящую значение переменной в него же. Если
получаем константу или тождественную функцию id, переводящую значение переменной в него же. Если 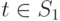 , то соответствующая функция является "простой". Истинные сложные функции появляются, начиная со слоя
, то соответствующая функция является "простой". Истинные сложные функции появляются, начиная со слоя 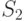 .
.
Заметим, что заданная интерпретация терма t одновременно определяет интерпретацию каждого терма, входящего в t.
Представим процесс вычисления сложной функции 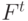 с помощью отмеченного графа
с помощью отмеченного графа 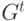 . Строится два представления: статическое (все результаты промежуточных вычислений располагаются на графе) и динамическое (шаг за шагом, слой за слоем).
. Строится два представления: статическое (все результаты промежуточных вычислений располагаются на графе) и динамическое (шаг за шагом, слой за слоем).
Пусть задана интерпретация терма t и определены значения всех переменных, входящих в t. Тогда для любого терма 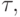 входящего в t, также задана интерпретация и определены значения всех функций
входящего в t, также задана интерпретация и определены значения всех функций 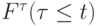 . Каждой вершине
. Каждой вершине 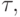 входящей в граф
входящей в граф 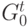 , сопоставляется значение функции
, сопоставляется значение функции 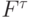 - элемент D. При этом вершинам нулевого слоя соответствуют значения переменных и констант, а единственной вершине последнего (выходного) слоя - значение
- элемент D. При этом вершинам нулевого слоя соответствуют значения переменных и констант, а единственной вершине последнего (выходного) слоя - значение 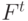 . Будем называть элементы D, соответствующие вершинам, значениями этих вершин и обозначать их
. Будем называть элементы D, соответствующие вершинам, значениями этих вершин и обозначать их 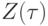 .
.
Для каждой вершины 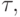 принадлежащей ненулевому слою, можно выписать уравнение функционирования, связывающее значения вершин. Пусть
принадлежащей ненулевому слою, можно выписать уравнение функционирования, связывающее значения вершин. Пусть 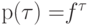 ,
,  и
и  - совокупность входящих в
- совокупность входящих в  ребер. Напомним, что совокупность меток ребер, оканчивающихся в
ребер. Напомним, что совокупность меток ребер, оканчивающихся в 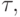
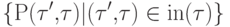
образует разбиение множества {1,2,...,k}.
Уравнение функционирования для вершины 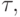 принадлежащей ненулевому слою, имеет вид
принадлежащей ненулевому слою, имеет вид
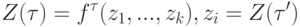 |
( 4) |
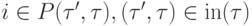
В силу уравнения функционирования (4), если для входящих в  ребер
ребер  известны значения
известны значения 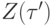 и задана интерпретация символа
и задана интерпретация символа 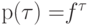 - метки вершины, то можно найти значение вершины
- метки вершины, то можно найти значение вершины 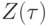 . На основании этого (очевидного) замечания строится динамическое представление вычисления сложной функции.
. На основании этого (очевидного) замечания строится динамическое представление вычисления сложной функции.
С каждой вершиной графа 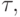 принадлежащей ненулевому слою, ассоциируется автомат, вычисляющий функцию
принадлежащей ненулевому слою, ассоциируется автомат, вычисляющий функцию 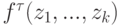 , где
, где  - метка вершины
- метка вершины 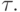 Автоматы срабатывают по слоям в дискретные моменты времени (такты) - автоматы i -го слоя в i -й момент времени. В начальный момент сформированы значения вершин нулевого слоя - известны значения переменных и констант. Они поступают на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i -го такта функционирования определены значения вершин, принадлежащих слоям
Автоматы срабатывают по слоям в дискретные моменты времени (такты) - автоматы i -го слоя в i -й момент времени. В начальный момент сформированы значения вершин нулевого слоя - известны значения переменных и констант. Они поступают на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i -го такта функционирования определены значения вершин, принадлежащих слоям 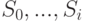 . На i+1 -м такте автоматы i+1 -го слоя вычисляют значения вершин i+1 -го слоя, получая входные сигналы с предыдущих слоев по правилу (4) - в соответствии с метками входящих ребер.
. На i+1 -м такте автоматы i+1 -го слоя вычисляют значения вершин i+1 -го слоя, получая входные сигналы с предыдущих слоев по правилу (4) - в соответствии с метками входящих ребер.
