Быстрое дифференцирование, двойственность и обратное распространение ошибки

Основную роль в последней сумме играет первое слагаемое - именно им определяется сложность обратного распространения по графу (если все , то T_Dif =cE, а уже в случае, когда , мы получаем T_Dif =2cE ). Поэтому можно положить 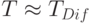(строго говоря, 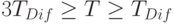, однако различия в два-три раза для нас сейчас несущественны).

Если характерное число переменных у простых функций, соответствующих вершинам графа, равно m (то есть 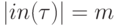), то для вычисляемой по графу сложной функции F можно оценить отношение затрат на вычисление F и gradF следующим образом:

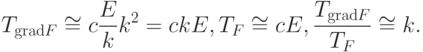
Эта оценка, конечно, лучше, чем полное число переменных n, но все же искомое отношение оценивается примерно как отношение числа ребер к числу вершин E/V (с точностью до менее значимых слагаемых). Если нас интересуют графы с большим числом связей, то для сохранения эффективности вычисления градиентов нужно ограничиваться специальными классами простых функций. Из исходных предположений 1-3 наиболее существенно первое ( 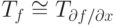). Зададимся вопросом: для каких функций f вычисление частных производных вообще не требует вычислений?

Ответ очевиден: общий вид таких функций

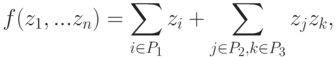( 12)

где множества индексов P₁, P₂, P₃ не пересекаются и, кроме того, P₂, P₃ имеют одинаковое число элементов. Значения всех частных производных таких функций уже известны, а источники (адреса) этих значений указываются связями графа. Какие-то значения z_k во второй сумме могут быть константами (значения нулевого слоя), какие-то - независимыми переменными (также нулевой слой) или значениями, найденными при промежуточных вычислениях.

В общем случае функции (12) билинейны. Их частный случай - линейные функции: если индексам из P₂ в (12) соответствуют константы, то функция f - линейная.

И функции вида (12), и соответствующие им вершины будем называть квазилинейными.

Пусть интерпретация функциональных символов такова, что в графе вычислений присутствуют только вершины двух сортов: квазилинейные или с одной входной связью (соответствующие простым функциям одного переменного). Обозначим количества этих вершин V_q и V₁ соответственно. Оценка сложности вычисления градиента для таких графов принципиально меняется. Обратное функционирование в этом случае требует следующих затрат:

1. Поиск всех производных функций одного переменного, соответствующих вершинам графа (число таких производных равно V₁ ), сложность поиска одной производной оценивается как c.
2. Вычисление всех произведений (7) на ребрах - E произведений.
3. Вычисление всех сумм (6) - сложность равна E-(V-V_out).

Итого, суммарная сложность обратного прохождения сигналов оценивается как

T gradF = cV 1+2E-(V- V out).

Оценим сложность вычислений при прямом распространении:

1. Для любой квазилинейной вершины сложность вычисления функции оценивается как ,
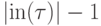2. Для любой вершины с одной входной связью сложность оценивается как c.

Итак, для прямого распространения сложность оценивается как

T F =cV 1+(E- V 1- V q).

С ростом числа связей !!

Графы вычислений (с заданной интерпретацией функциональных символов), в которых присутствуют только вершины двух сортов: квазилинейные или с одной входной связью (соответствующие простым функциям одного переменного) играют особую роль. Будем называть их существенно квазилинейными. Для функций, вычисляемых с помощью таких графов, затраты на вычисление вектора градиента примерно вдвое больше, чем затраты на вычисление значения функции (всего!). При этом число связей и отношение 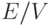могут быть сколь угодно большими. Это достоинство делает использование существенно квазилинейных графов весьма притягательным во всех задачах оптимизации. Их частным случаем являются нейронные сети, для которых роль квазилинейных вершин играют адаптивные линейные сумматоры.

Таким образом, обратное прохождение адаптивного сумматора требует таких же затрат, как и прямое. Для других элементов стандартного нейрона обратное распространение строится столь же просто: точка ветвления при обратном процессе превращается в простой сумматор, а нелинейный преобразователь 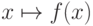в линейную связь 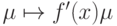с коэффициентом связи 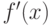. Поэтому для нейронных сетей обратное распространение выглядит особенно просто. Детали можно найти в различных руководствах, например [3.5, 3.6]

Отличие общего случая от более привычных нейронных сетей состоит в том, что можно использовать билинейные комбинации (12) произвольных уже вычисленных функций, а не только линейные функции от них с постоянными коэффициентами-весами.

В определенном смысле квазилинейные функции (12) вычисляются линейными сумматорами с весами 1 и 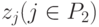и аргументами и 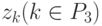, только веса не обязательно являются константами, а могут вычисляться на любом слое.

Естественно возникает вопрос о вычислительных возможностях сетей, все вершины которых являются квазилинейными. Множество функций, вычисляемых такими сетями, содержит все координатные функции и замкнуто относительно сложения, умножения на константу и умножения функций. Следовательно оно содержит и все многочлены от любого количества переменных. Любая непрерывная функция на замкнутом ограниченном множестве в конечномерном пространстве может быть сколь угодно точно приближена с их помощью.