Решение задач нейронными сетями

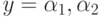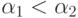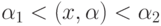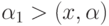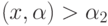Если это уравнение имеет два корня , ( ) то наилучшим решающим правилом будет: при объект принадлежит одному классу, а при или - другому (какому именно, определяется тем, которое из произведений 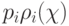больше). Если корней нет, то оптимальным является отнесение к одному из классов. Случай единственного корня представляет интерес только тогда, когда . При этом уравнение превращается в линейное и мы приходим к исходному варианту - единственной разделяющей точке .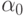

Таким образом, разделяющее правило с единственной разделяющей точкой 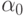не является наилучшим для нормальных распределений и надо искать две разделяющие точки.

Если сразу ставить задачу об оптимальном разделении многомерных нормальных распределений, то получим, что наилучшей разделяющей поверхностью является квадрика (на прямой типичная "квадрика" - две точки). Предполагая, что ковариационные матрицы классов совпадают (в одномерном случае это предположение о том, что ), получаем линейную разделяющую поверхность. Она ортогональна прямой, соединяющей центры выборок не в обычном скалярном произведении, а в специальном: 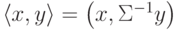, где - общая ковариационная матрица классов. За деталями отсылаем к прекрасно написанной книге [2.17], см. также [2.11, 2.12, 2.16].

Важная возможность усовершенствовать разделяющее правило состоит с использовании оценки не просто вероятности ошибки, а среднего риска: каждой ошибке приписывается "цена" c_i и минимизируется сумма 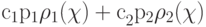. Ответ получается практически тем же (всюду p_i заменяются на c_i p_i ), но такая добавка важна для многих приложений.

Требование безошибочности разделяющего правила на обучающей выборке принципиально отличается от обсуждавшихся критериев оптимальности. На основе этого требования строится персептрон Розенблатта - "дедушка" современных нейронных сетей [2.1].

Возьмем за основу при построении гиперплоскости, разделяющей классы, отсутствие ошибок на обучающей выборке. Чтобы удовлетворить этому условию, придется решать систему линейных неравенств:

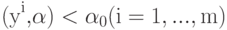
Здесь xⁱ ( i=1,..,n ) - векторы из обучающей выборки, относящиеся к первому классу, а yⁱ ( j=1,..,m ) - ко второму.

Удобно переформулировать задачу. Увеличим размерности всех векторов на единицу, добавив еще одну координату - 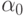к , x₀=1 - ко всем x и y₀ =1 - ко всем y. Сохраним для новых векторов прежние обозначения - это не приведет к путанице.

Наконец, положим zⁱ = xⁱ ( i=1,...,n ), z^j = -y^j ( j=1,...,m ).

Тогда получим систему n +m неравенств

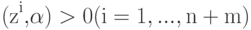
которую будем решать относительно . Если множество решений непусто, то любой его элемент порождает решающее правило, безошибочное на обучающей выборке.

Итерационный алгоритм решения этой системы чрезвычайно прост. Он основан на том, что для любого вектора x его скалярный квадрат (x,x) больше нуля. Пусть - некоторый вектор, претендующий на роль решения неравенств 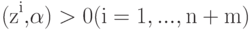, однако часть из них не выполняется. Прибавим те zⁱ, для которых неравенства имеют неверный знак, к вектору и вновь проверим все неравенства 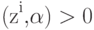и т.д. Если они совместны, то процесс сходится за конечное число шагов. 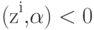Более того, добавление zⁱ к можно производить сразу после того, как ошибка ( ) обнаружена, не дожидаясь проверки всех неравенств - и этот вариант алгоритма тоже сходится [2.2].